\(\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Di}[1]{\mathop{}\!\mathrm{d}#1\,} \newcommand{\Dd}[1]{\frac{\mathop{}\!\mathrm{d}}{\mathop{}\!\mathrm{d}#1}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle}\)

This lecture is intended for students of the “Licence de physique”, and in particular to those interested in theoretical physics.

Maxwell demon and Landauer principle

Maxwell discusses in his Theory of Heat (1871) the validity of the second principle of thermodynamics using a thought experiment, in the following terms:

[…] if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.

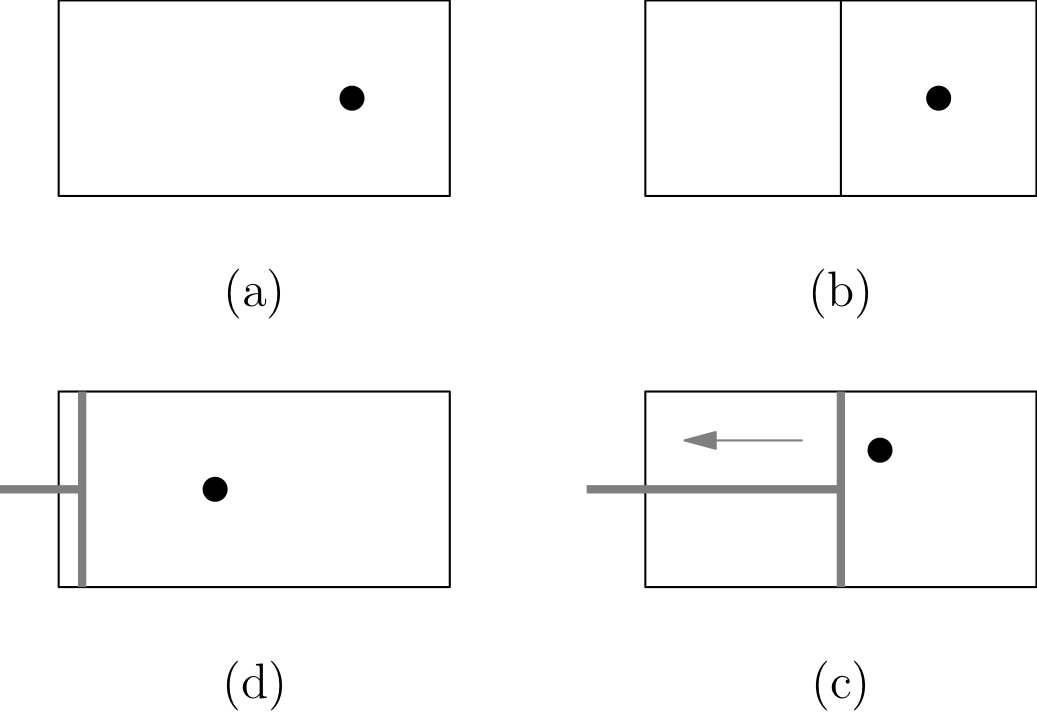
This statement is known as the “Maxwell Demon”. Szilard (1937) gave a simplified version, schematically represented in the figure:

Initially a “gas” particle is inside a volume \(V\) at temperature \(T\) (a); in (b) a wall separating the volume in two equal compartments is introduced; (c) a demon records the position, left or right, of the particle in the box; if the particle is on the right, the demon places a piston, for instance linked to a resort, on the other side: the expansion from \(V/2\) to \(V\) of the particle (gas) exerts a force that can compress the resort; in the final state (d) we find, as in the initial state, a particle in \(V\). As a result we extracted work \(W\) from the system at fixed temperature, decreasing then the system’s entropy

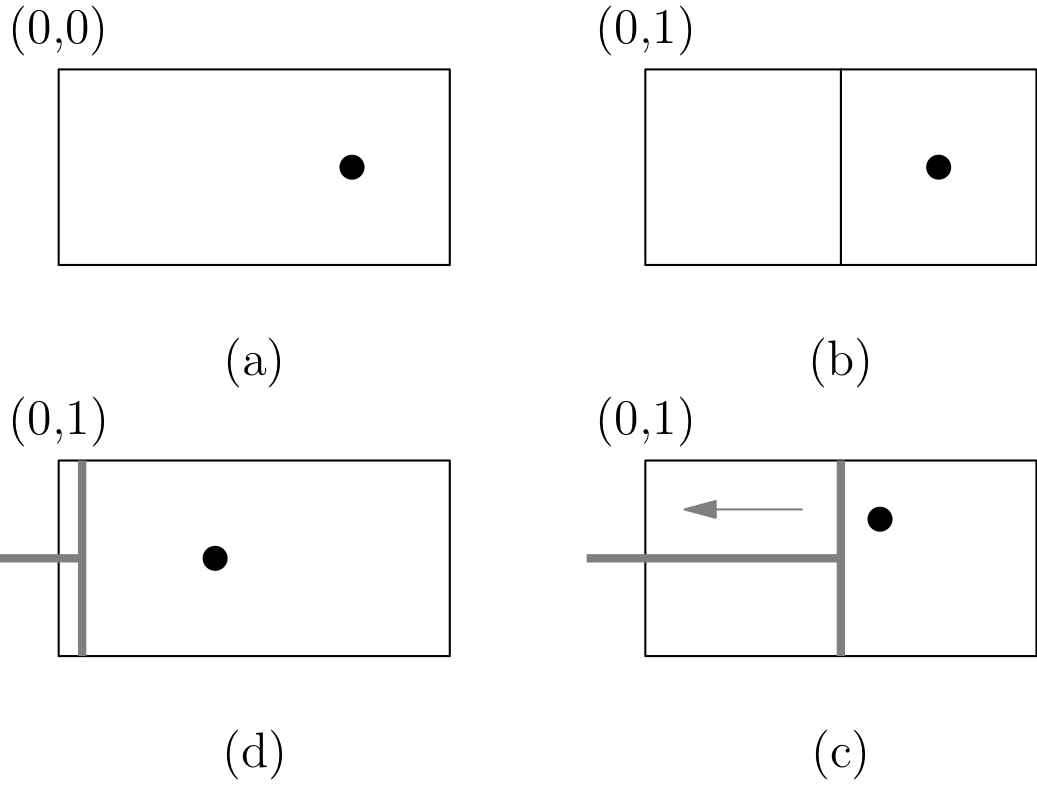
in apparent contradiction with the second principle. However, we must include in the analysis the state of the demon:

The demon starts in a state \((0,0)\), so its registers correspond to \(0\) particles on the left and \(0\) on the right (a); in (b) its state changes: the right compartment is filled with one particle \((0,1)\); its state do not change and in (d) it is always \((0,1)\). Therefore, the whole (isolated) system, consisting on the particle and the demon, do not return to its initial state in (d). In order to recover the initial state we need to erase the registers of the demon. This fundamental observation was first pointed out by Bennett in 1982¹. Yet, erasure of a register implies entropy growth! This deep statement was first proposed by Landauer in 1961², and is now known as the Landauer principle. It states that information is a physical property, it is always carried by some physical device; the physical action corresponding to erase a bit has a cost in entropy:

This increase in the entropy of the demon exactly compensates the entropy decrease in the system: hence, the whole system entropy remains constant, in accordance with the second principle:

An experimental confirmation of the Landauer principle was first demonstrated by Bérut et al. (2012)³, using a colloidal particle trapped in a double well potential as a stochastic model of a single bit.

Particle in a double well potential

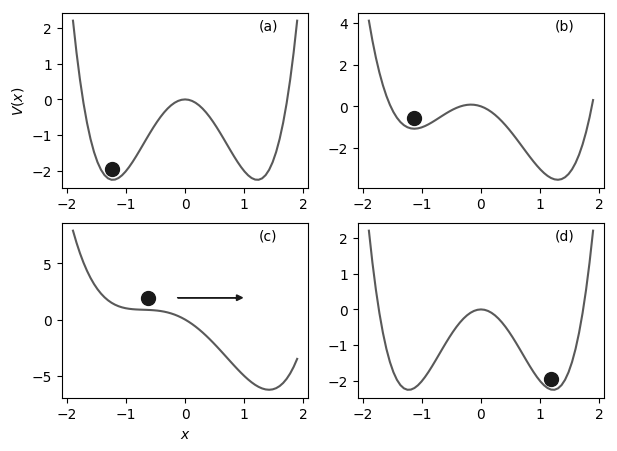
A particle in a double well potential has two stable states that can be interpreted as a physical model of an information bit: the left well might represent a \(0\) state, and the right well the \(1\) state of the bit. Using a modulation of the potential parameters one can modify the respective deeps of the wells, and end up with say, the \(1\) state, whatever the initial state \(0\) or \(1\), erasing thus the information contained in the initial state.

Particle in a double well potential \(V(x) = cx - ax^2 + bx^4\) with \(a=3\), \(b=1\) (a). The system can store a bit of information according to the position of the particle. The particle initial state is \(0\), and, after modulation of the potential shape (changing the parameter \(c\), in this case), the particle state changes to \(1\), \(c=0,-1,-3,0\) for (a,b,c,d), respectively. If the particle had being at \(1\) initially, the final result would be the same: the initial state is thus erased after a cycle (a,b,c,d). Adapted from Berut et al. (2012).³

The system is considered in equilibrium with a thermal bath at fixed temperature \(T\). Therefore, the particle dynamics can be described by a Langevin equation:

where \(\gamma\) is the friction coefficient with dimension of mass over time, and \(F(t)\) represents the stochastic force, whose correlation function is proportional to the bath temperature:

The particle diffusion coefficient is given by the Einstein relation \(D = 2 k_\mathrm{B}T/\gamma\).

An important property of the langevin equation is that, for time independent potential, the probability distribution of the random variable \(x\) tends in the long time limit, to a stationary law, given by the boltzmann distribution:

where \(Z\) is a normalization constant. Indeed, on can demonstrate that the probability distribution satisfies the Fokker-Planck equation,

where

is the deterministic force acting on the particle. For long times the stationary solution is precisely the boltzmann distribution EX.

In our case, the force depends explicitly on time \(f=f(x,t)\), to take into account the shape deformation of the potential wells. One may investigate numerically the behavior of the particle for different temperatures. The lifetime \(\tau\) of the bit, a colloidal particle in a double well, depends on the hight of the potential barrier \(\Delta E\), as given by an Arrhenius type law (which is a consequence of the boltzmann formula given above):

it is then exponentially long at low temperatures \(\Delta E \ll k_\mathrm{B}T\), but rapidly decreases with the augmentation of the temperature. The energy barrier is roughly given by the difference in energy between the unstable state and the stable one of the potential energy.

In the general case with a time dependent potential, it is convenient to use a numerical method to study the system’s behavior. The following python code integrates the langevin equation using a simple euler method. One can store the final position of the particle \(x_t\) and plot its histogram to verify if the erasing is effective.

T = 0.4 # temperature
tf = 100 # cycle time
x0 = -1.5 # intital position
N = 1000

dt = 0.01 # time step
sdt = np.sqrt(dt)
NT = np.int(tf/dt)
xt = x0*np.ones(N)
np.random.seed(2001)
#
# trajectory
for it in range(NT):
    t = it*dt
    xt += dt*(12.0*np.sin(np.pi*(T-t)**2/T**2)*np.ones(N) + \
                              8*xt - 4*xt**3) + \
                              2*T*sdt*np.random.normal(0, 1, N)

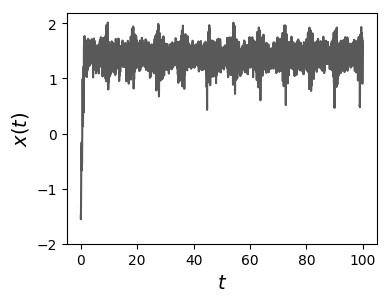
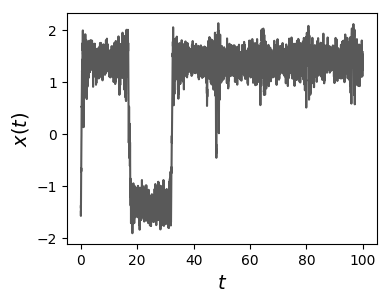
Using the results of the numerical integration we observe that, depending on the temperature for fixed values of the potential parameters, the protocol is effective in erasing the initial position.

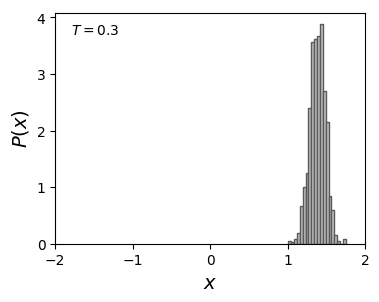
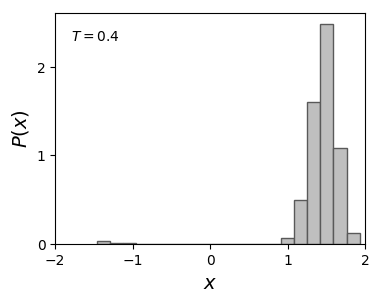
Histogram and typical trajectory of a colloidal particle at temperature \(T\), under the influence of a time dependent force that temporarily suppress the left well (the particle is initialized at this well), favoring the right well position at long times. At high temperature, spontaneous transition between the two wells can occur, introducing errors in the erasure process (as seen in the figures for \(T=0.4\)).

At \(T=0.3\) all trajectories, initially on the left well (state \(0\)), end at the right well (state \(1\)). A small amount of error appears at \(T=0.4\).

That the erasure is a dissipative process is demonstrated by the necessity to introduce, to modify the potential, an external time dependent force. The landauer principle says us that the concomitant entropy growth must be larger than \(\Delta S > k_\mathrm{B}\ln 2\). It is precisely this fact that was verified by Berut et al. (2012) experiments.³

Bibliography

• Plenio, M. B., and Vitelli, V., “The physics of forgetting: Landauer’s erasure principle and information theory,” Contemporary Physics 42, 25 (2000) (.pdf)

• Maruyama, K., Nori, F., and Vedral, V., “The physics of Maxwell’s demon and information,” Rev. Mod. Phys. 81, 1 (2009) (.pdf)

Notes