Leçon de physique théorique: la marche aléatoire

jeu. 25 février 2016
Blog
#teaching

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Di}[1]{\mathop{}\!\mathrm{d}#1\,} \newcommand{\Dd}[1]{\frac{\mathop{}\!\mathrm{d}}{\mathop{}\!\mathrm{d}#1}}$

Texte destiné aux étudiants de la troisième année de la licence de physique particulièrement intéressés par la physique théorique.

La physique est une science quantitative, l’expérimentateur étudie les phénomènes de la nature mettant en évidence des propriétés mesurables et dégageant des régularités qui peuvent s’exprimer sous la forme des lois empiriques. La physique théorique a pour objectif d’inférer à partir des données de l’expérience, mais aussi avec le cadre théorique déjà établit, les concepts scientifiques; sa tâche est de relier les concepts physiques par des lois mathématiques. Nous voyons que la physique se construit historiquement: les connaissances expérimentales (mesures) et leur expression théorique (concepts) et mathématique (lois) s’élargissent en fonction des découvertes, parfois même en remettant en cause les bases établies par des nouvelles observations, et montrant donc la nécessité de reviser les fondements jusqu’alors considérés comme justes.

La physique s’occupe donc des phénomènes mesurables, ce qui s’exprime par le fait que les grandeurs physiques ont des dimensions, comme les grandeurs mécaniques (longueur, temps, masse, énergie) ou thermodynamiques (température, pression, entropie). Or, les lois de la physique sont indépendantes du système d’unités utilisé pour mesurer ces grandeurs (mètre, seconde, kilogramme, joule, etc.).

Nous avons défini la physique théorique, faisons en maintenant usage: posons nous la question si c’est possible de traduire par une loi mathématique cette indépendance vis-à-vis de l’unité des lois physiques.

Pensons à deux grandeurs $x$ et $y$; la loi physique est mathématiquement une fonction

$$y=f(x)\,.$$

Changer les unités revient à une homothétie:

$$x\rightarrow X=ax\,,\quad y\rightarrow Y=by\,.$$

L’indépendance de la loi s’exprime par l’invariance de la fonction $f$ vis-à-vis de l’homothétie:

$$y=f(x) \quad \Rightarrow \quad Y=f(X)=bf \left(\frac{X}{a}\right)\,.$$

Nous avons obtenu une equation dont la solution à trouver est la fonction $f$; nous constatons qu’elle implique une certaine relation entre les paramètres, au départ arbitraires, $a$ et $b$; en effet, après calcul nous trouvons que la solution s’écrit,

$$f(x) = f(1) x^\alpha\,,\quad \alpha = \frac{\ln b}{\ln a}\,,$$

c’est-à-dire, une loi de puissance ($f(1)$ est une constante, bien sûr). Nous avons donc établi une loi de la nature: les grandeurs physiques (dimensionnées) sont reliées par des lois de puissance!

Nous illustrons maintenant, à travers l’exemple de la marche aléatoire, une caractéristique de la physique, et en particulier, de la façon dont la physique théorique se construit: un problème simple et apparemment sans connexion évidente avec la complexité de la nature, permet d’expliquer des phénomènes comme la diffusion, mais aussi, en généralisant au monde quantique, d’aborder le domaine de l’informatique quantique. Voyez vous un rapport entre les deux?

La marche aléatoire

Un marcheur a le choix, selon le résultat pile ou face du jet d’une pièce de monnaie, de faire un pas vers la gauche ou vers la droite. Voici posé le problème: quelle est la position du marcheur parti de l’origine $x=0$, au bout de $t$ jets? La réponse ne peut être que probabiliste, puisque sa position va dépendre de l’évènement aléatoire de la séquence pile-face.

Nous pouvons aborder le problème à partir de différents points de vue; nous pouvons par exemple, calculer la valeur moyenne de la position $\overline{x}(t)$ ou sa variance $\overline{x^2}(t)$ en fonction du nombre de pas (temps); ou nous pouvons aussi essayer de calculer la probabilité $P(x,t)$ de trouver le marcheur en $x$ au temps $t$.

Nous allons supposer dans un premier temps que la position et le temps sont des entiers $x,t\in \mathbb{Z}$ (marche discrète), ce qui revient à mesurer les longueurs en unités de pas $\Delta x$ et le temps en unités de la durée entre deux jets $\Delta t$. La position à $t+1$ est

$$x(t+1) = x(t) + b(t)\,, \quad b(t)= \begin{cases} 1, &\text{ si }p=1/2\\ -1, &\text{ si }p=1/2 \end{cases}\,,$$

où $b(t)$ est un “processus stochastique”, qu’on appelle parfois un bruit blanc (dans la limite où le temps est continu, $|\Delta t \rightarrow 0$):

$$\overline{b(n)}=0\,,\quad \overline{b(n)b(m)}=\delta_{n,m}$$

où $n=0,1,\ldots,t$ et $\delta_{n,m}$ la delta de Kronecker.

La position au bout de $t$ jets est par conséquent,

$$x(t) = \sum_{n=1}^{t} b(n)\,.$$

La valeur moyenne est immédiatement calculée en utilisant $\overline{b}=0$, ou d’une façon équivalente, en remarquant que pour chaque temps on a $\overline{x}(t+1)= (x(t)-1)/2 + (x(t)+1)/2=x(t)=x(0)=0$.

La variance se déduit de l’indépendance des jets:

$$\overline{x^2}(t)=\sum_{n,m}^{t}\overline{b(n)b(m)}= \sum_{n,m}^{t}\delta_{n,m}=t\,.$$

Avec ce simple calcul nous avons un résultat important: le marcheur s’éloigne de l’origine non pas comme un mobile ayant une vitesse constante $x\sim t$, mais en raison de la racine du temps

$$x \sim \sqrt t\,,$$

c’est-à-dire, une loi de puissance. Cette loi est caractéristique de la diffusion, le phénomène de mélange d’un polluant dans l’air, ou de la chaleur dans un métal. Si on rétablit les unités, on obtient la relation,

$$ \overline{x^2}(t) = \frac{(\Delta x)^2}{\Delta t} t \equiv D t$$

où nous avons introduit le coefficient de diffusion $D$.

Le lien avec la diffusion devient plus évident quand on calcule la probabilité $P(x,t)$. En effet, la définition de la marche aléatoire se traduit dans l’équation de recurrence,

$$P(x,t+\Delta t) = \frac{1}{2}P(x+\Delta x,t) + \frac{1}{2}P(x-\Delta x,t)\,,$$

pour la distribution de probabilité de la position. Cette équation peut être utilisée pour calculer la limite continue de la marche aléatoire:

$$\Delta x \rightarrow 0\,,\quad \Delta t \rightarrow 0\,.$$

Dans cette limite nous obtenons effectivement l’équation de la diffusion

$$\frac{\partial }{\partial t}f(x,t) = \frac{D}{2} \frac{\partial^2 }{\partial x^2} f(x,t)$$

avec

$$D= \lim_{\Delta x, \Delta t \rightarrow 0} \frac{(\Delta x)^2}{\Delta t}$$

le coefficient de diffusion, et la condition de normalisation,

$$\int_{-\infty}^{\infty} \Di{x} f(x,t) =1$$

de la fonction de distribution $f=\lim P/\Delta x$ de la position.

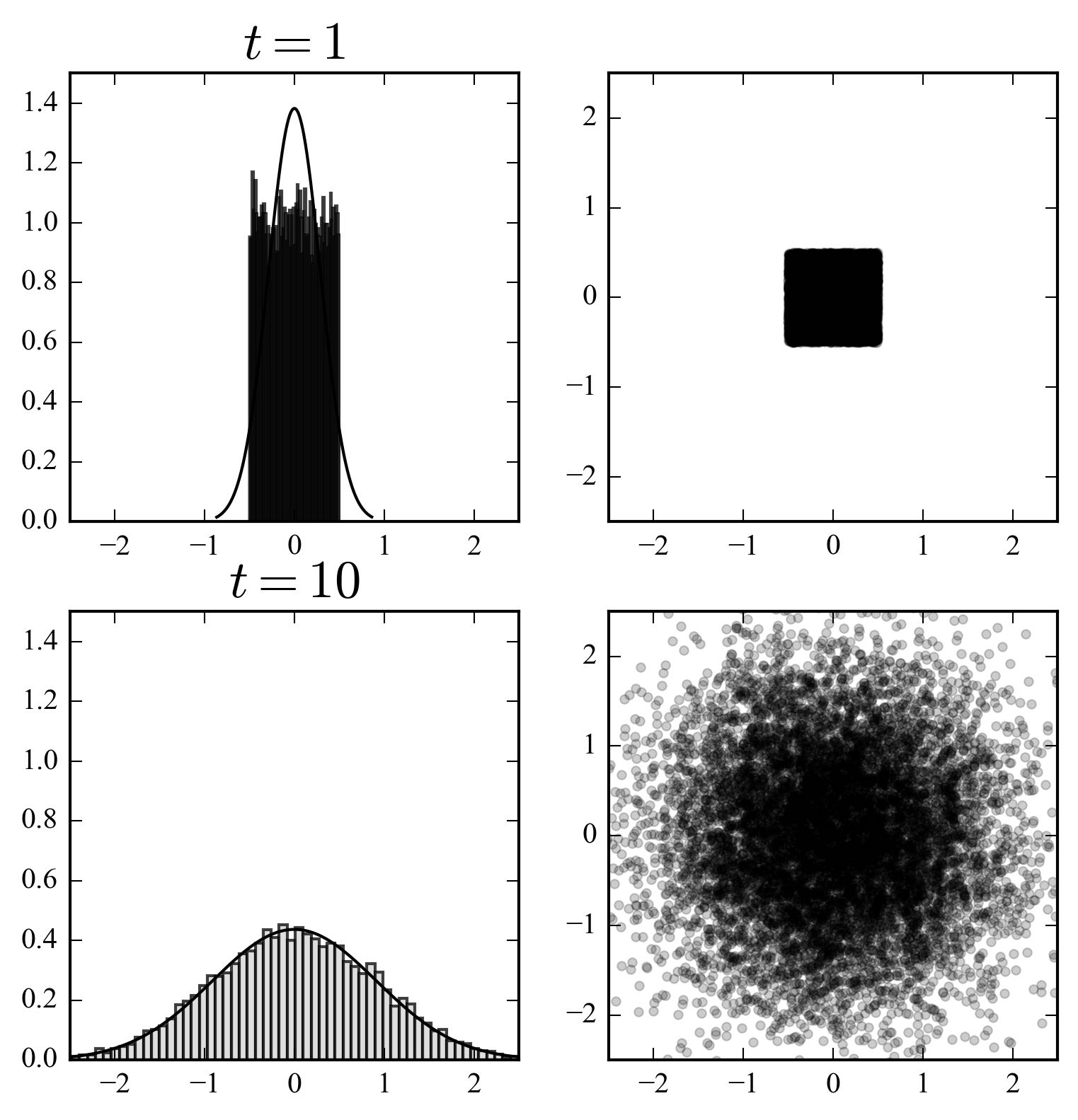
La figure montre la projection sur le plan des positions de 10000 marcheurs dans l’espace, se trouvant au pas 1 dans le cube de côté 1, et à temps 10 dans une sphère. La distribution de postions, initialement uniforme dans le carré, devient rapidement proche de sa valeur “continue”, c’est-à-dire gaussienne, comme le montre l’histogramme. L’étalement des marcheurs est caractéristique du phénomène de diffusion.

Marche quantique

Une démarche habituelle de la physique théorique est d’utiliser un résultat connu et de l’appliquer dans un autre contexte physique (analogie) ou de le rendre applicable à un autre domaine expérimental (généralisation). Dans notre exemple, nous allons généraliser la marche aléatoire discrète au cas quantique en utilisant un raisonnement par analogie.

À la place du marcheur, nous considérons un état quantique $|\psi(t)\rangle$ qui dépend à la fois de la position, que nous allons changer à l’aide d’un opérateur $S$ de translation spatiale d’une unité, et d’un degré de liberté interne, comme le spin, qui nous servira pour décider la direction à prendre. La pièce de monnaie peut-être donc remplacée par un opérateur qui agit sur le spin. Les ingrédients de la marche quantique sont:

Marcheur: l’état quantique $|\psi\rangle = |x\rangle \otimes |s\rangle$, produit tensoriel des états de position $x \in \mathbb{Z}$ et de spin $s=\uparrow,\downarrow$. Cet état va évoluer selon un temps discret $t \in \mathbb{Z}$.
Pièce de monnaie: opérateur de Hadamard représenté par la matrice
$$A = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \,.$$
Une fois appliquée sur, par exemple, un état pur
$$A|\uparrow\rangle= A\begin{pmatrix} 1\\0 \end{pmatrix}= \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\1 \end{pmatrix}\,,$$
nous obtenons un état de superposition de deux orientations du spin. Cette état superposé est une caractéristique quantique, sans équivalent classique.
Pas de la marche: l’opérateur
$$S=\sum_x \left( |x+1\rangle \langle x|\otimes |\uparrow\rangle\langle\uparrow| + |x-1\rangle \langle x|\otimes |\downarrow\rangle\langle\downarrow| \right)$$
déplace l’état vers la gauche si le spin est down et vers la droite s’il est up. Il conduit aussi vers un état de superposition, cette fois sur la position du marcheur (qui fini par se “trouver” sur plusieurs positions au pas $t$).
Évolution: le produit des opérateurs “pièce” et “déplacement”, nous donne l’opérateur,
$$U = S(I \otimes A)$$
qui determine un pas de la marche (l’unité $I$ a la dimension de l’espace de positions):
$$|\psi(t+1)\rangle = U |\psi(t)\rangle\,.$$
Cet opérateur étant unitaire, détermine bien une dynamique quantique.
Mesure: au bout d’un nombre de pas $t$ l’état du marcheur est mesuré par le projecteur $M$ sur la position $|y\rangle$:
$$M = |y \uparrow\rangle \langle y \uparrow | + |y \downarrow\rangle \langle y \downarrow|\,.$$
C’est précisément cette mesure qui révèle le caractère aléatoire quantique de la marche: elle permet d’obtenir la probabilité pour le marcheur de se trouver en $y$ au pas $t$:
$$ P(y,t) = \langle\psi(t)|M|\psi(t)\rangle\,.$$

Le code suivant, montre une implémentation numérique en langage python de la marche quantique.

def hadamard(N):
    u = ones(2*N + 1)/sqrt(2)
    return array([[u,u],[u,-u]]) # spin x spin x pos

def init_psi(N, a, b):
    """Initial state $x = 0, x \in [-N, N]$"""
    psi = zeros((2, 2*N + 1), dtype = complex)
    A = sqrt(abs(a)**2 + abs(b)**2) # norm
    psi[0,N] = a/A # x[N] = 0
    psi[1,N] = b/A
    return psi # spin x pos

def qw_hadamard(N, a = 1, b = 0):
    """Hadamard quantum walk.

    Ex: N = 60 steps with initial state |0>:
        psi_t = qw_hadamard(60, a = 1, b = 0)
    """
    c = hadamard(N)
    psi = init_psi(N, a, b)
    # 
    psi_t = zeros((2, 2*N + 1, N + 1), dtype = complex)
    psi_t[:,:,0] = psi
    for n in arange(1, N+1):
        psi1 = einsum('ijk,jk->ik', c, psi) # coin step
        psi[0] = roll(psi1[0], 1) # shift step (up)
        psi[1] = roll(psi1[1], -1) # shift step (down)
        psi_t[:,:,n] = psi
    return psi_t # spin x pos x time

def measure(psi):
    return abs(psi[0])**2 + abs(psi[1])**2

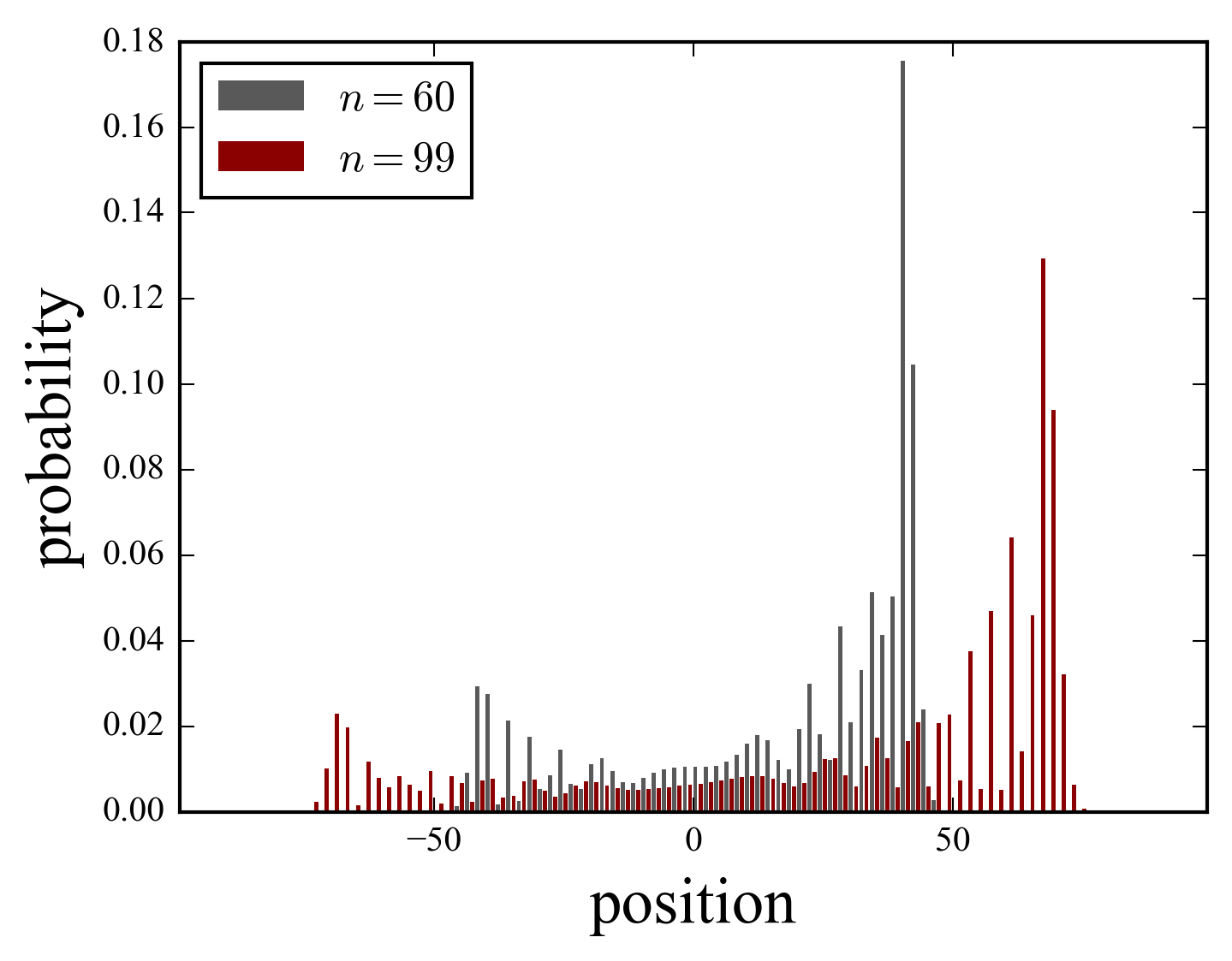
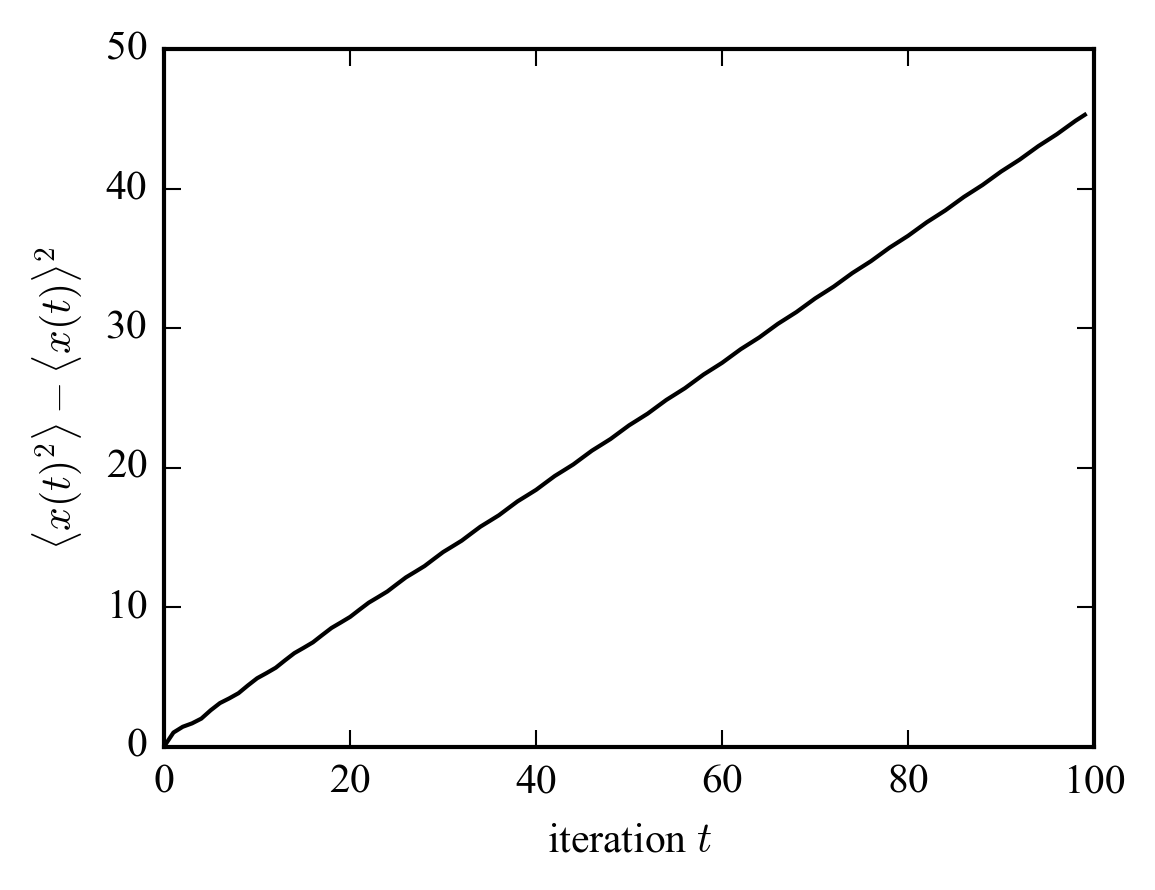
Les figures montrent la distribution de probabilité de la position du marcheur et l’écart type en fonction du temps. Nous avons choisi un état initial pur avec un spin up en $x=0$; cela se traduit par un mouvement dont la probabilité se concentre à droite de l’origine. La première figure montre la probabilité à deux temps ($t=60,100$), où nous remarquons l’asymétrie introduite par la condition initiale (phénomène exclusivement quantique). Nous voyons en plus que l’écart type de la deuxième figure croît comme $t$, en non en $\sqrt(t)$, comme dans le cas classique.

Conclusion

À travers l’exemple de la marche aléatoire nous pouvons dégager un aspect caractéristique de la démarche théorique en physique: une formulation simple d’un problème bien posé, inspiré de l’observation ou de l’expérience, sert de point d’appui à des généralisations capables de révéler des phénomènes et des effets insoupçonnés. La cohérence de la démarche est assurée par la cohérence mathématique. L’intérêt et la validité des résultats dépendent de leur capacité à rendre compte des phénomènes observés tout comme à leurs possibilités d’application et d’extension à des problèmes hors de leur cadre initial.