Nonlinear disordered quantum walk

lun. 02 mai 2016
Blog
#research

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}}$

Work in progress to investigate the edge states of a quantum walk at the interface between two topologically distinct regions, when spatial disorder is present. Published in EPJB, 2017.

Topological phases of matter appeared with the discovery of the quantum Hall effect. A quantum walk having the same topological properties as the anomalous quantum Hall system, was discussed by Kitagawa et al recently. It is defined by the product

\begin{equation} \label{e:tr} U = T_x R(\theta) T_y R(\alpha) T_{x+y} R(\theta) \end{equation}

of shift operators $T_i$, which move the walker’s position a single step $\pm1$ in the direction $i=x,y$ of a square lattice according to their spin state, and rotation operators

\begin{equation} R(\theta) = \E^{-\I \theta \sigma_y/2} = \begin{pmatrix} \cos \theta/2 & -\sin \theta/2 \\ \sin \theta/2 & \cos \theta/2 \end{pmatrix} \,, \end{equation}

which rotate the $1/2$ particle’s spin by $\theta$ around the $y$-axis ($\boldsymbol \sigma$ are Pauli matrices). Therefore, the quantum walk evolution is defined by the unitary operator $U$, which advances the particle’s state a time step:

\begin{equation} |\psi(t+1) \rangle = U \, |\psi(t)\rangle\,, \end{equation}

where $|\psi(t)\rangle$ is the quantum state of the walker at time $t$; initially

\begin{equation} |\psi(0)\rangle = |0\rangle \otimes \frac{|\uparrow\rangle + \I |\downarrow\rangle}{\sqrt{2}}\,, \end{equation}

the particle is at the origin in a superposition of spin up and down with equal probability. The first movie shows the propagation of the position probability:

\begin{equation} P(x,y,t) = |\psi_\uparrow(x,y,t)|^2 + |\psi_\downarrow(x,y,t)|^2 \,, \end{equation}

where $\psi_{\uparrow\downarrow}$ are the spinor components. As other realizations of quantum walks, the information propagates in a ballistic fashion.

As in the quantum Hall effect, one may compute the Chern number. Indeed, we can associate an effective Hamiltonian $H$ to the unitary operator:

\begin{equation} U = \E^{-\I H}, \quad H \equiv \I\,\log U\,, \end{equation}

which allows the study of the topological properties of the random walk using the same tools of condensed matter systems. According to the value of the angles $(\theta,\alpha)$, one finds that the Chern number takes one of the values $C \in \{-1,0,1\}$.

Topological properties

We consider a system with an interface separating a $C=-1$ left region (for $x < 0$) and a $C=1$ right region (for $x \gt 0$). In the figure we show the two representative points in the $(\theta,\alpha)$ phase plane, corresponding to each topological domain: red for the left and blue for the right. At the edge, localized modes exist that, in the case of the Hall system, are responsible for the conduction. These topologically protected bound states were experimentally observed in the case of a one dimensional quantum walk.

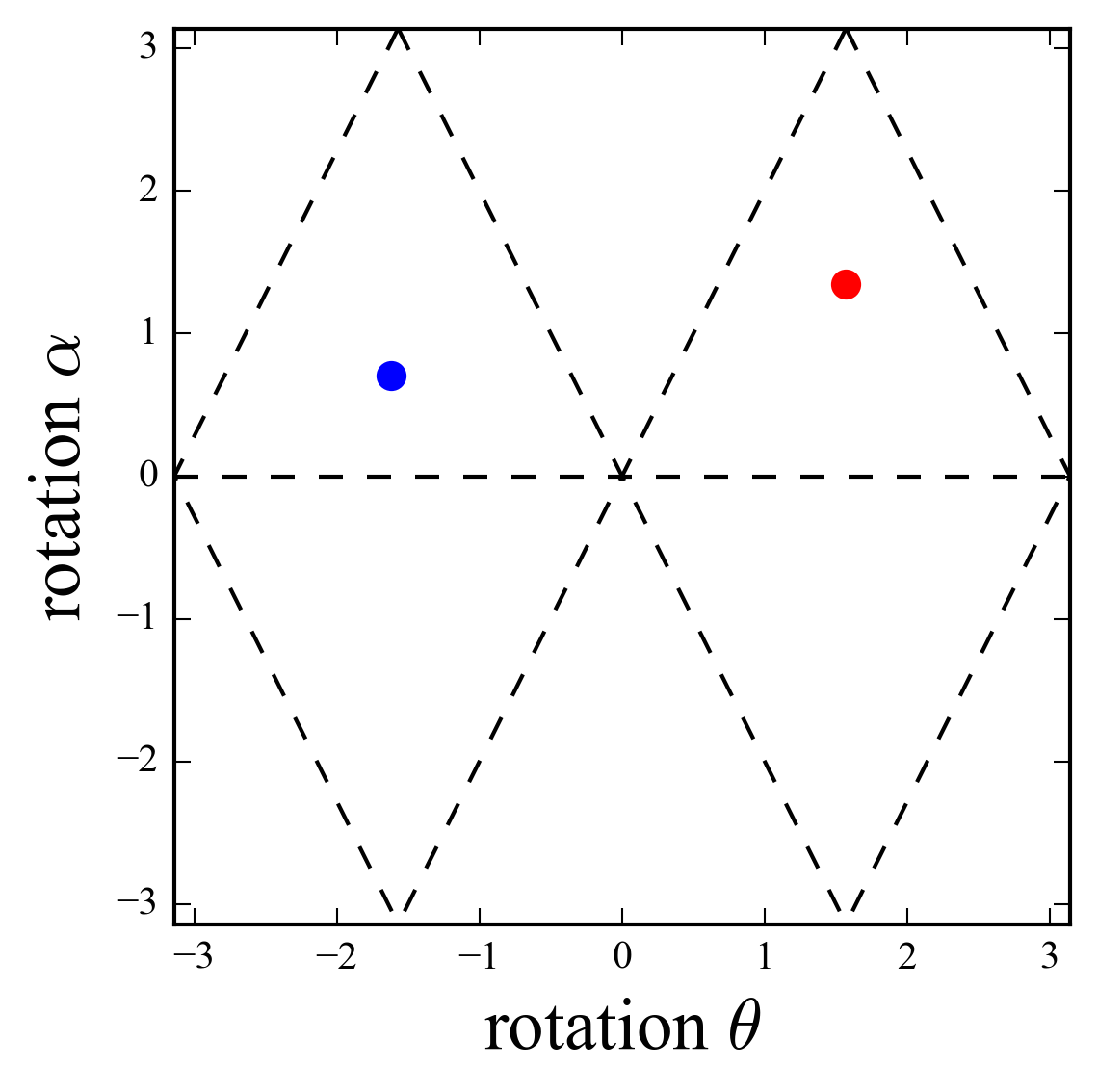
quantum walk topology spatial disorder

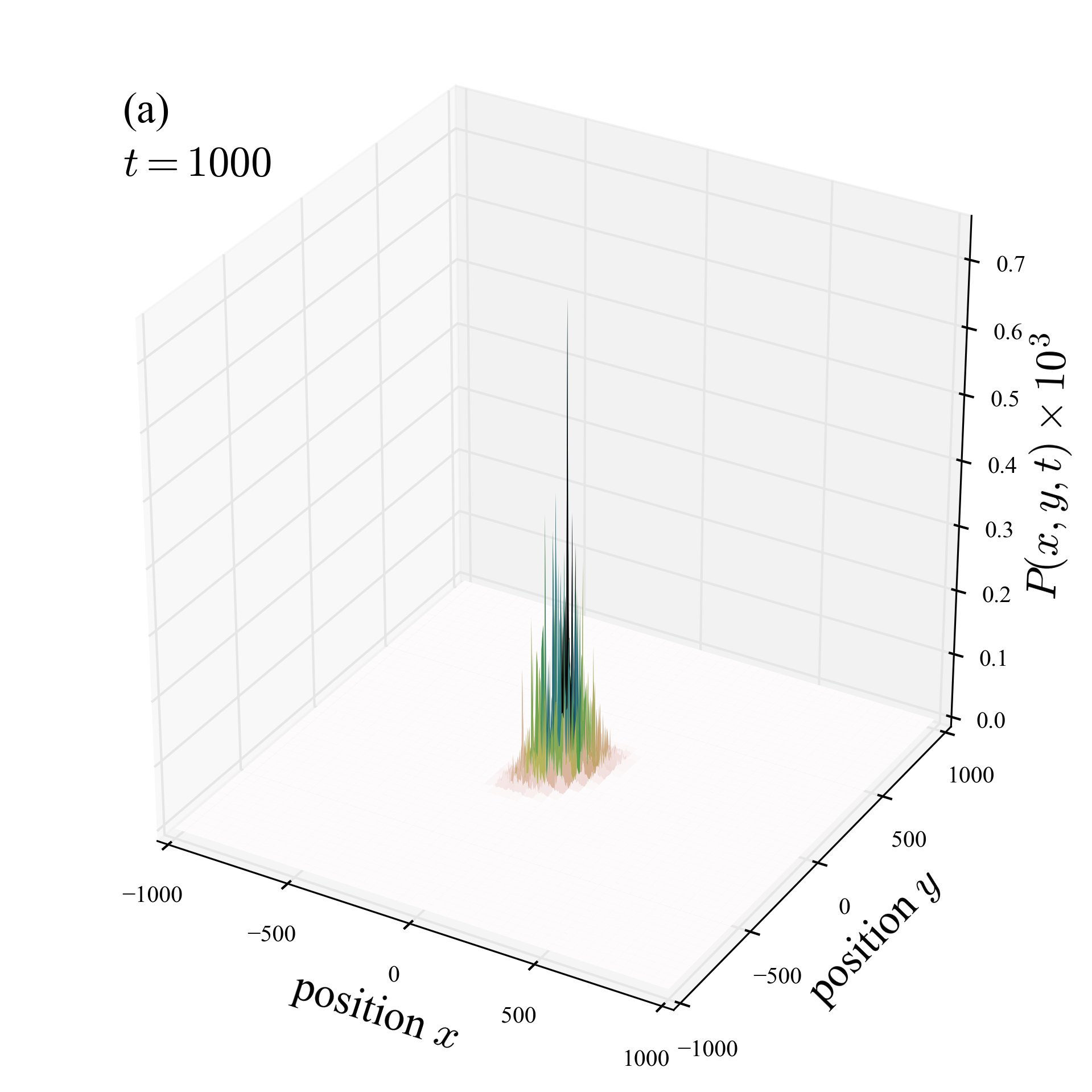
In the case of the two dimensional quantum walk $\ref{e:tr}$, we numerically computed the time evolution (second movie) and found that the position probability concentrates at the interface and spreads along the $y$ axis, in agreement with the existence of an edge state.

Effect of disorder

One important property of the edge states associated with the topology of the effective Hamiltonian (in analogy with the electronic bands of an insulator), is that they are protected against random perturbations. As long as the perturbation do not change the topology, for instance closing the gap or adding new states in the gap, the transport properties of the system are preserved.

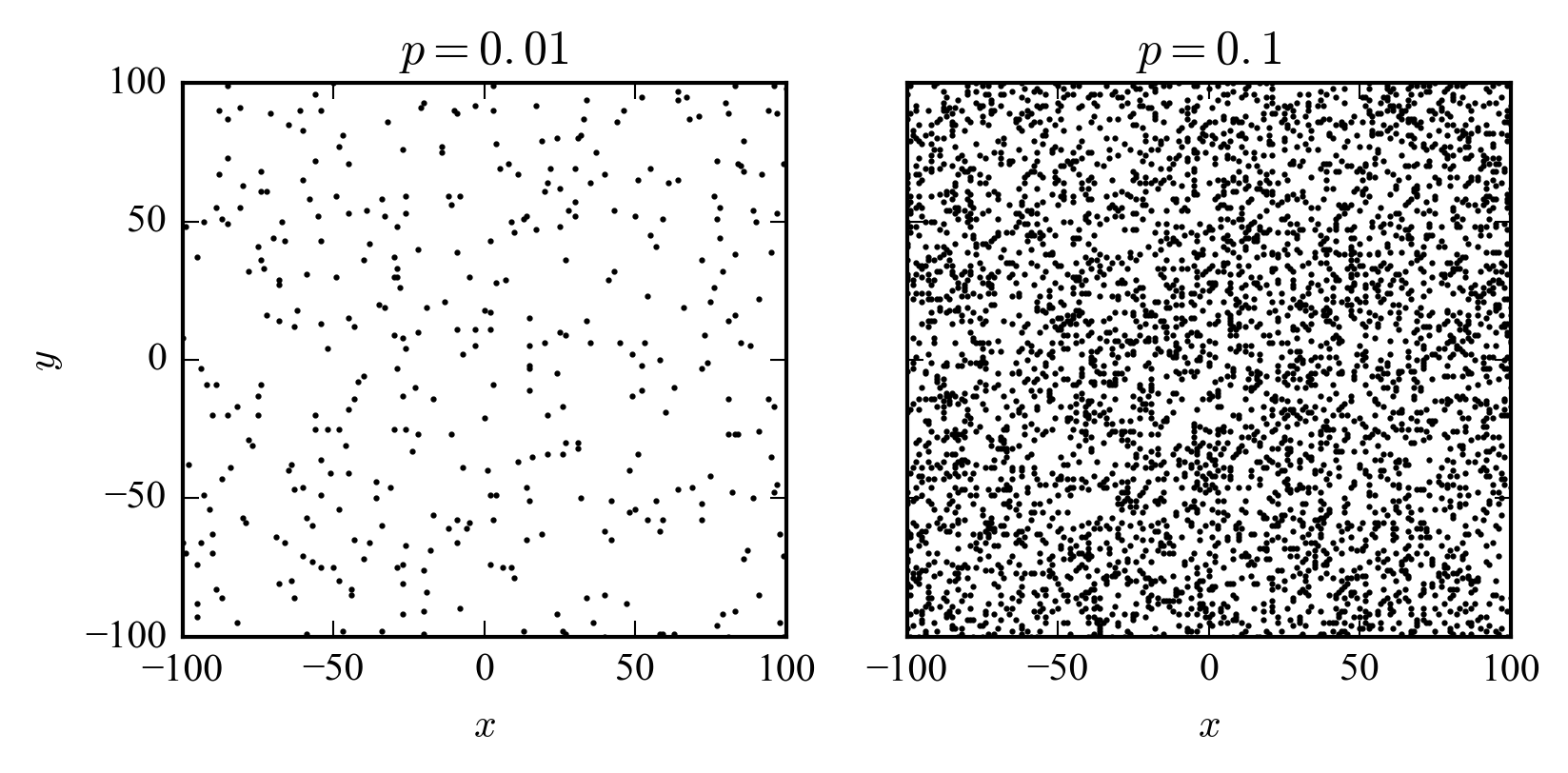
We are interested in investigating the behavior of the edge states in the case of the two-dimensional quantum walk $\ref{e:tr}$, when it is perturbed by spatial disorder. We introduce, at random sites uniformly distributed over the square lattice, a set of impurities $I$ (as shown in the figure, where we compare two sets with occupation probabilities $p=0.01$ and $p=0.1$). These impurities will change the spin state of the walker.

In the presence of disorder, we consider various modifications of the coin operator $R$:

the rotation angle becomes random, $\theta \rightarrow \theta + \delta\theta$,
$$R_J(\theta) = \E^{-\I \sigma_y (\theta + J\delta\theta(x))/2},\; x \in I\,,$$
where $J$ is a coupling constant and $\delta\theta$ is uniformly distributed on the circle (quenched “rotation” disorder);
the walker’s spin is changed by the impurity spin, polarized in the $z$ direction,
$$S_J(\phi) = \E^{-\I J \sigma_z \phi(x,t)},\; x \in I\,,$$
where the phase $\phi(x,t)$ can be randomly distributed on the circle (quench “spin” disorder, independent of time),
or dependent on the particle’s state (self-consistent disorder),
$$\phi(x,t) = |\psi_\uparrow|^2 - |\psi_\downarrow|^2$$
or
$$\phi(x,t) = \frac{|\psi_\uparrow|^2 - |\psi_\downarrow|^2}{ |\psi_\uparrow|^2 + |\psi_\downarrow|^2}\,. $$
In the first case the impurity phase is proportional to the $z$ component of the particle spin, and in the second case, it is in addition normalized to the local particle density; this second form is invariant with respect to scale transformations of the spinor. For the self-consistent disorder the coin operator writes:
$$R_J(\theta,\phi) = S_J(\phi)R(\theta)\,,$$
and the quantum walk becomes nonlinear. Nonlinear quantum walks are studied in relation to the Dirac equation; in particular solitons and attractors, were recently predicted.

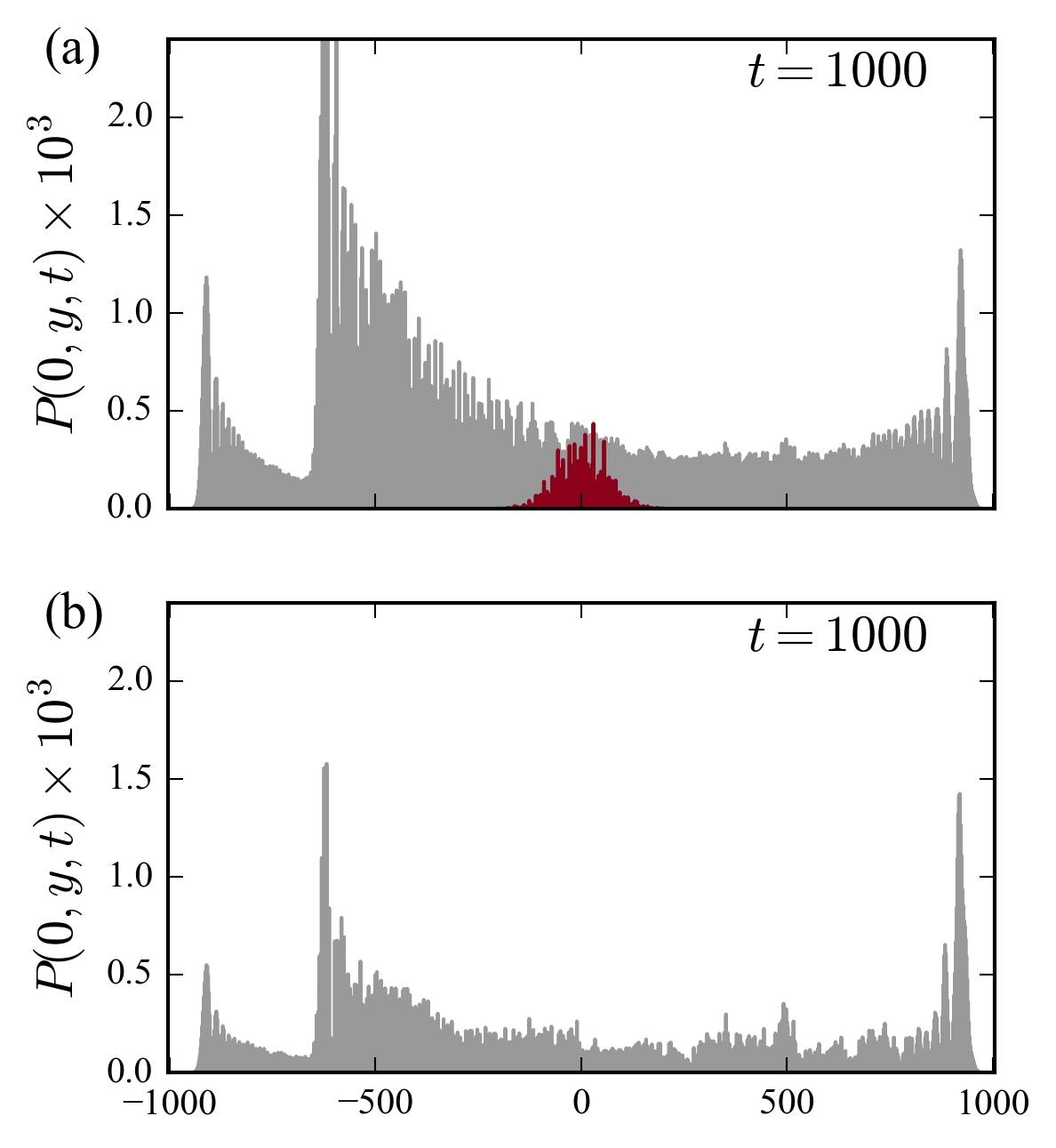
The two videos compare the probability density at the interface of the free (without disorder) and the random (with spatial disorder) quantum walks. The two cases show ballistic propagation on the edge state. The following two figures show the width of the probability at $x=0$ (spreading in the $y$ direction), for the free walk and the nonlinear walk with $p=0.1$ and $J=100$; we choose a large value of the coupling constant to strength the remarkable behavior in this case.

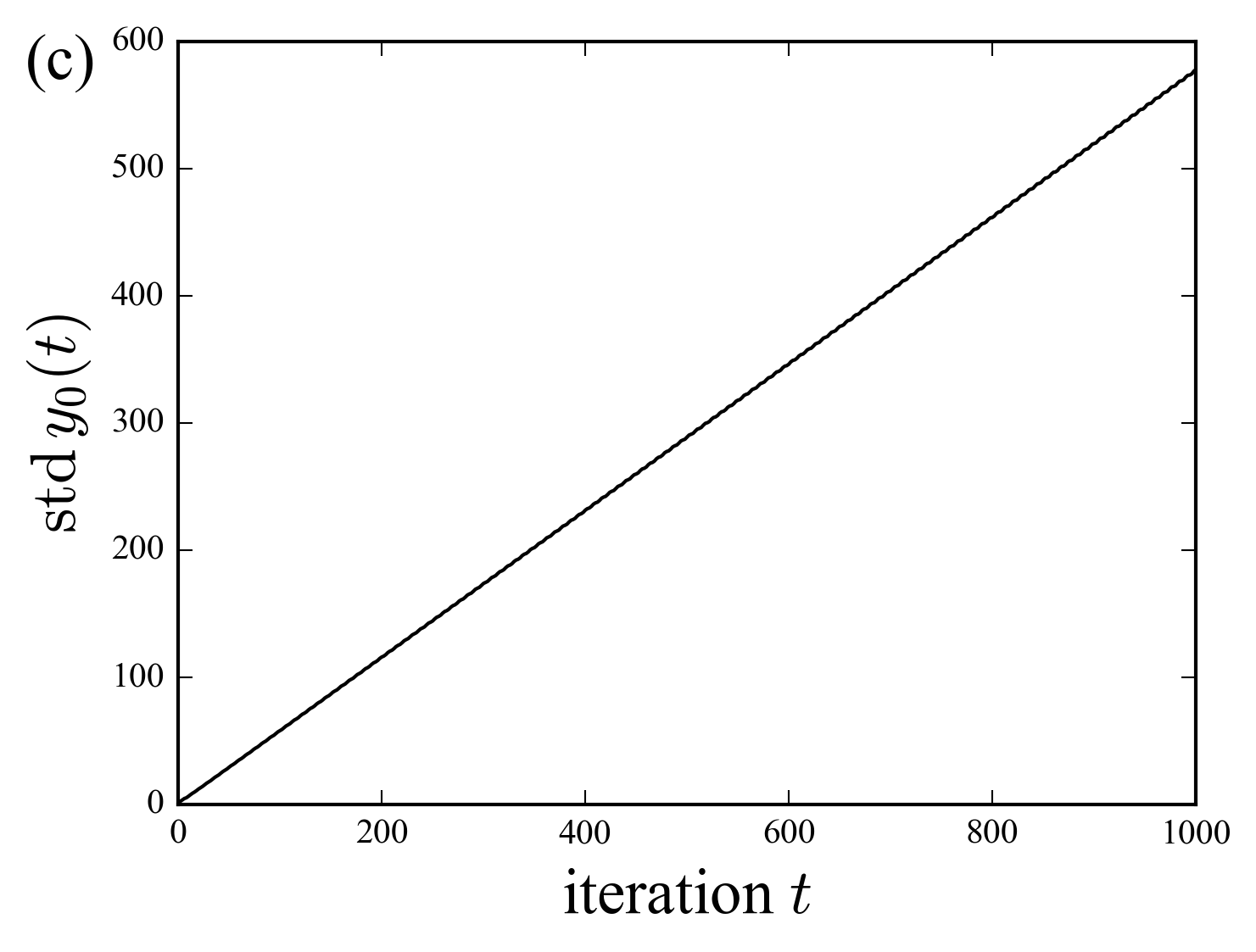
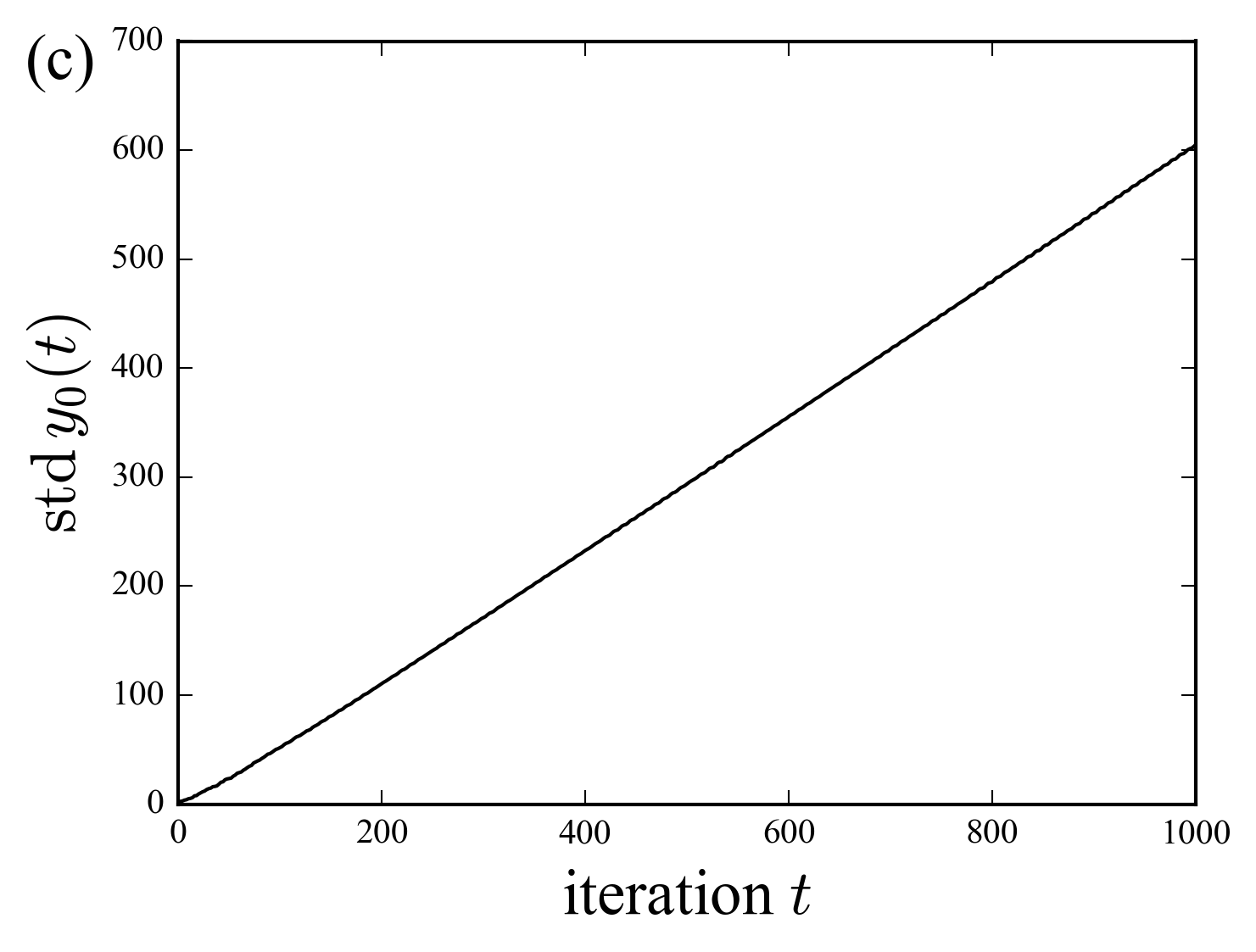
free walk on the edge random walk on the edge

Indeed, it its worth noting that the presence of the nonlinear disorder do not prevent the walker to spread at a rate proportional to the time. This is in contrast with the usual behavior of a quantum walk, which localizes or diffuse as a result of disorder.

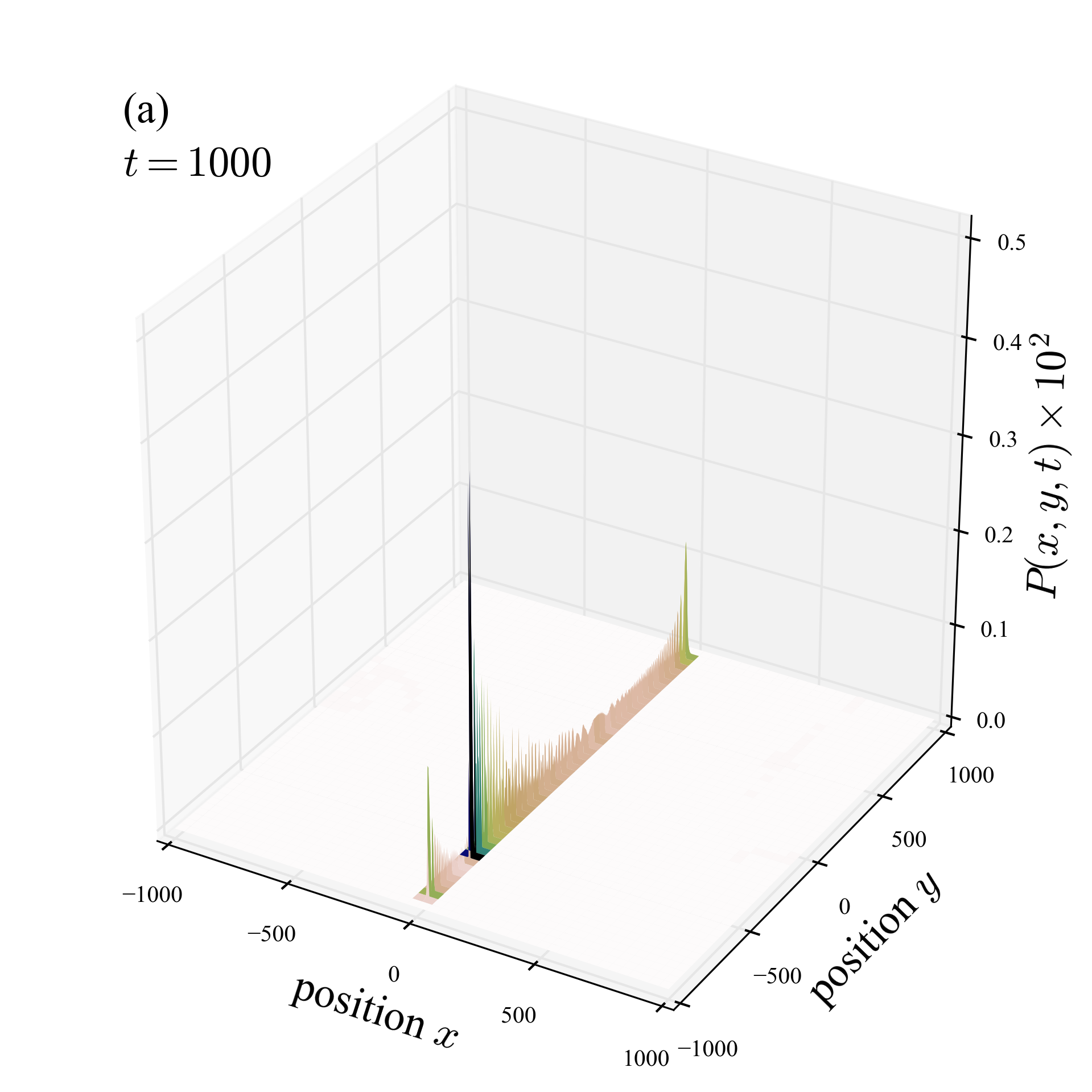
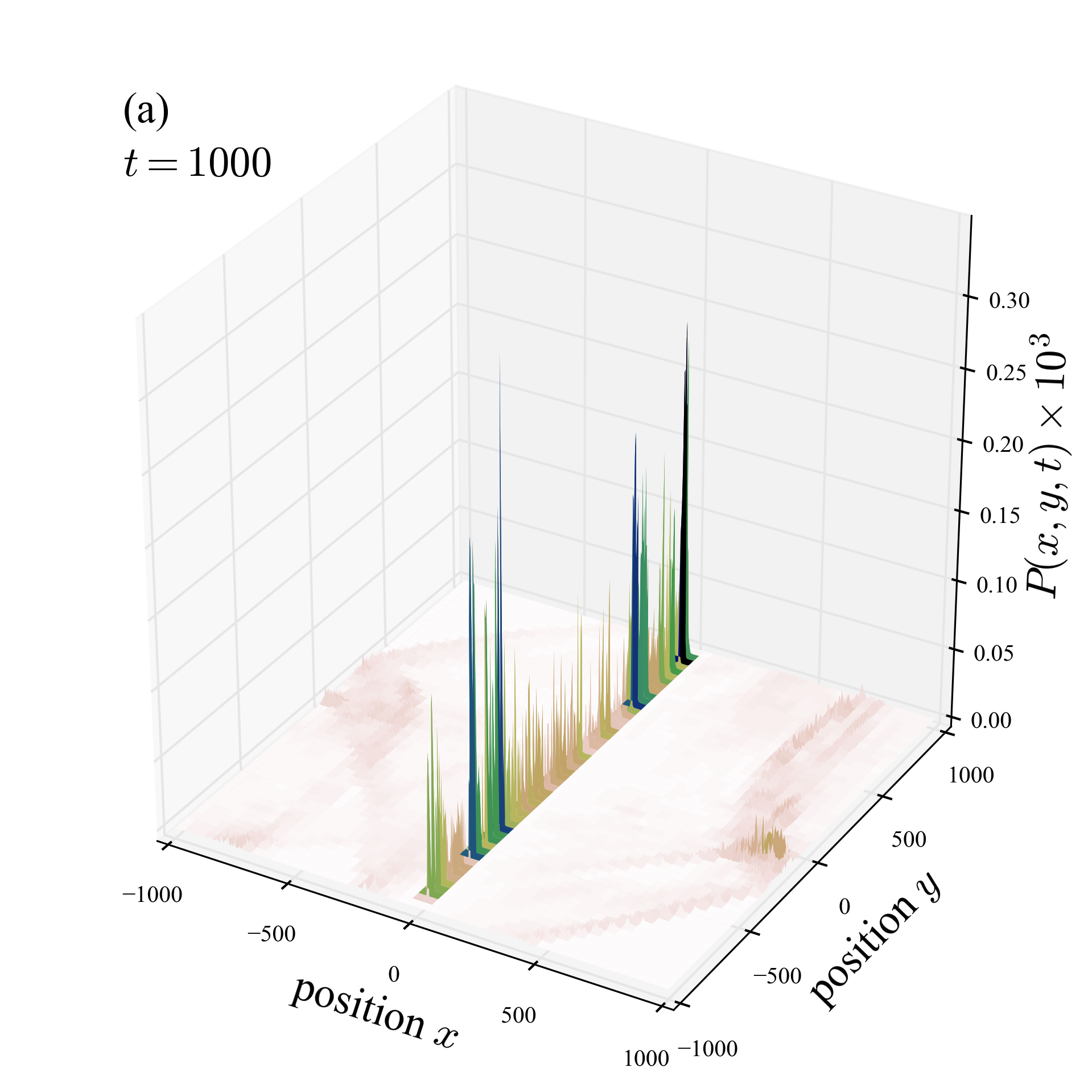
free walk on the edge random walk on the edge

We also observe, as shown in the figures above, that in the random case the probability density distribution is slightly larger than in the free case near the interface. This is probably an effect due to disorder induced (anisotropic) localization, the density is confined in a region around its initial position. However, the presence of the edge state, wider in the case of disorder, prevents the localization along the $y$ axis.

Noise and nonlinearity

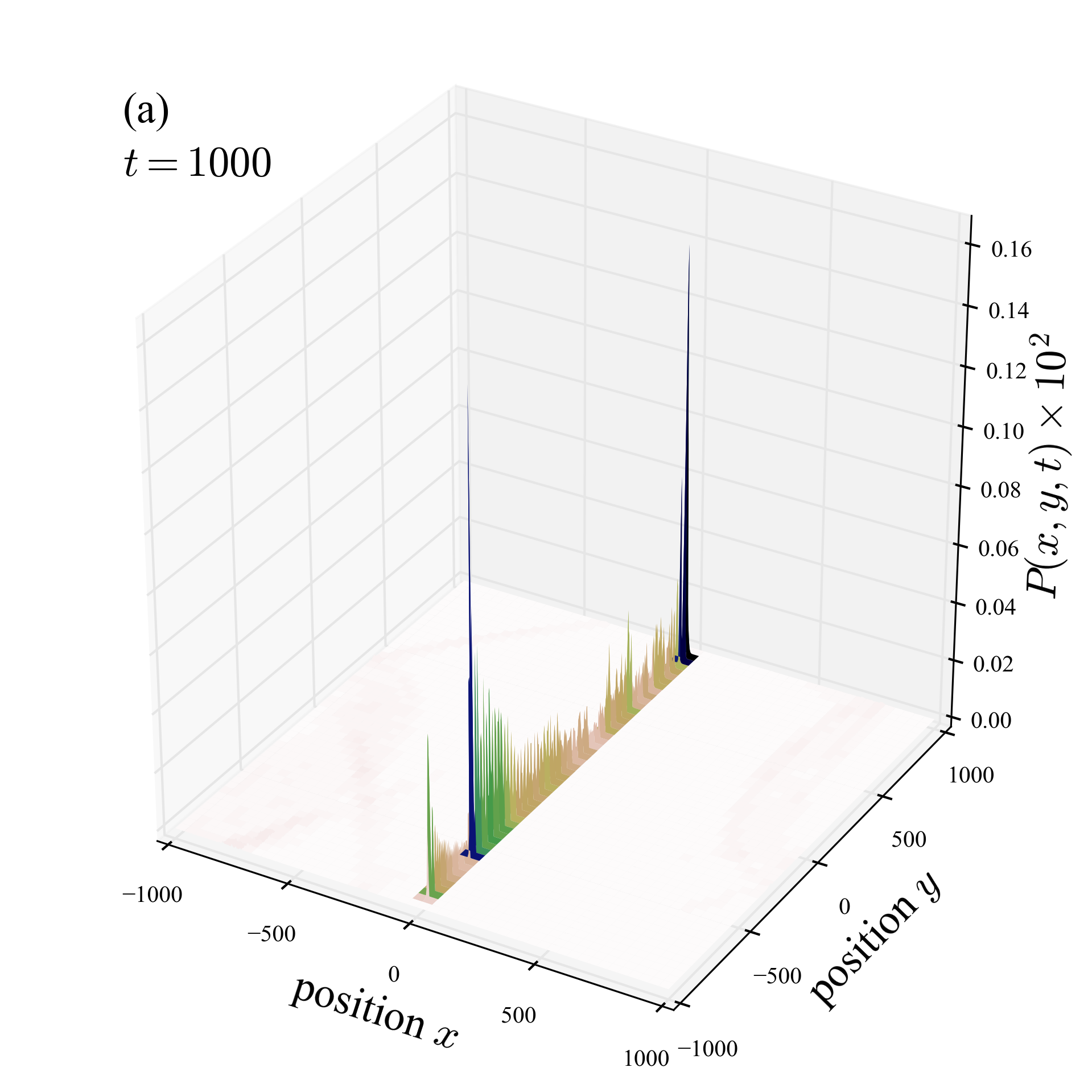
The edge state is protected against disorder. If the amplitude of the noise in the rotation angle is not large enough to change the topology of the system, the edge state persists. Strong disorder may destroy it.

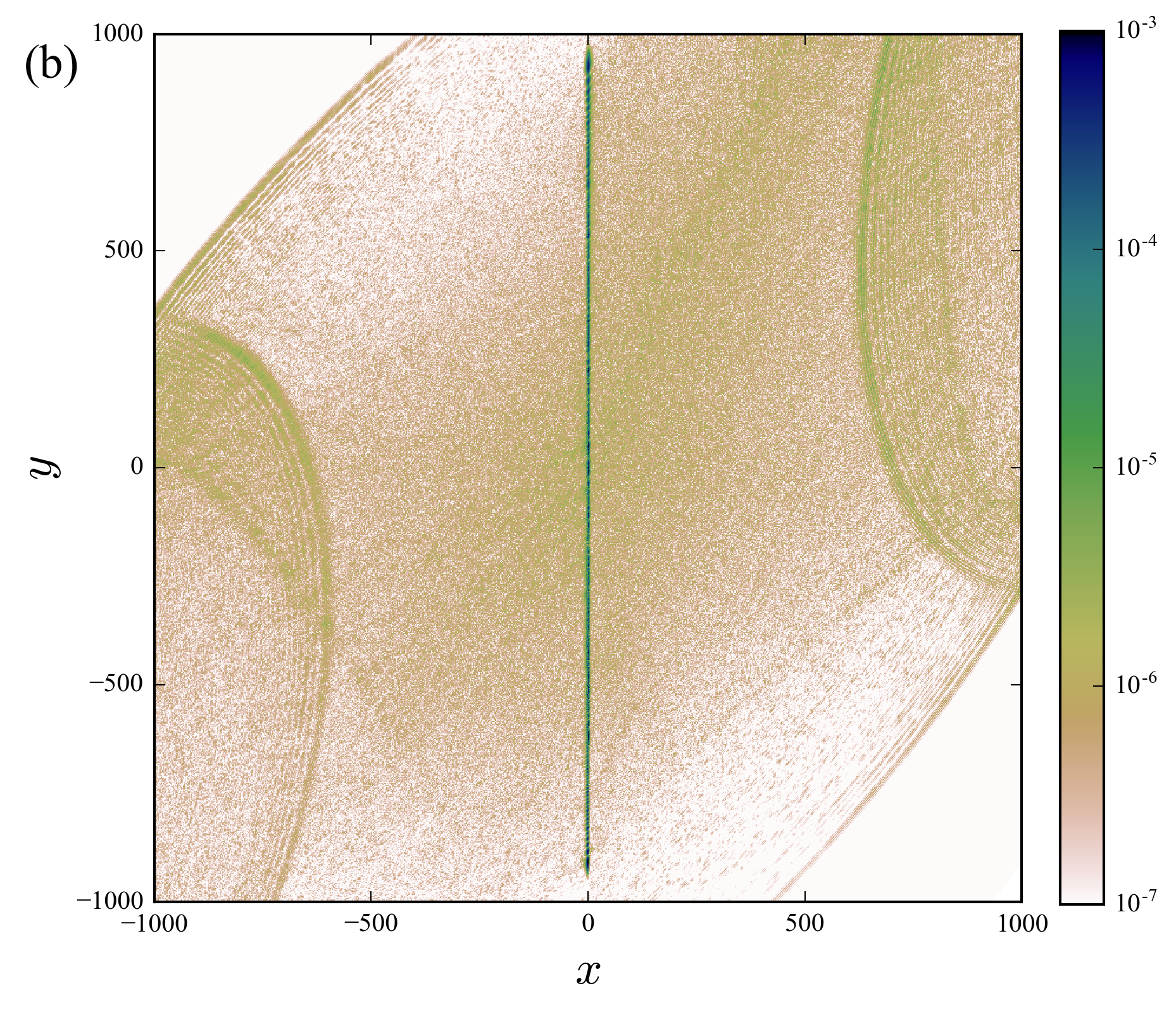
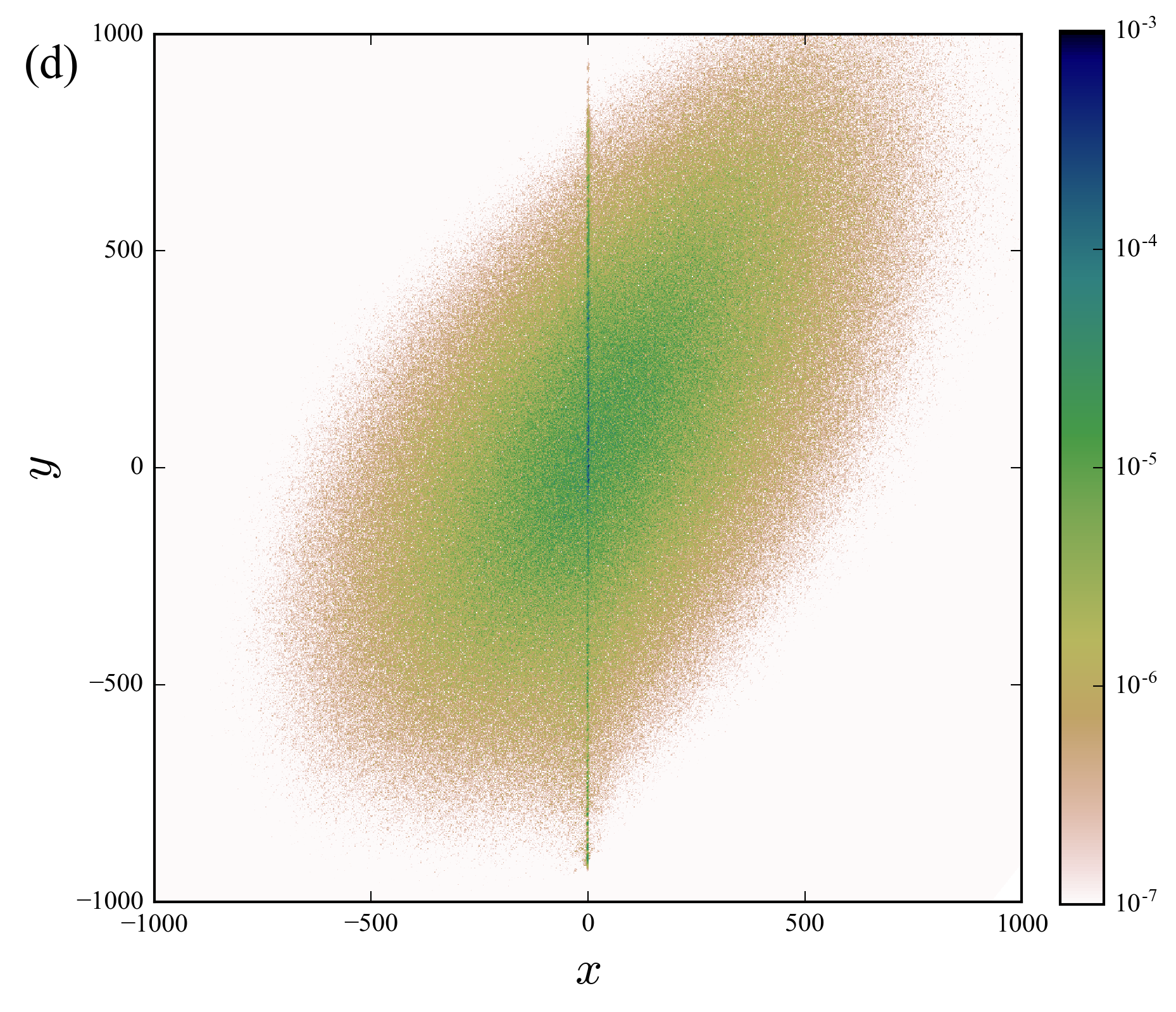
weak rotation noise strong rotation noise

Figures above compare the spreading of the walker in the weak ($p=0.05$) and strong ($p=0.2$) disorder cases.

The nonlinear walk restore the edge state even in the presence of strong noise.



Spreading along the interface in the case of nonlinear (gray) and linear $z$-phase noise (red) walks for the same parameters. Stronger noise (below panels) do not destroy the coherence of the nonlinear walk on the edge channel.