mer. 21 mars 2018
Blog
#research

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\PL}{{\!+}} \newcommand{\MI}{{\!-}} \newcommand{\ket}[1]{|#1\rangle} \newcommand{\bra}[1]{\langle#1|} \newcommand{\braket}[1]{\langle#1\rangle}$

Work in progress to investigate the interplay of topology and interaction in a simple quantum walk model. Work in collaboration with Gabriel Elías, Universidad de Santiago. Now published in SciPost (2018).

Interacting split-step quantum walk

A quantum system of two particles is defined by the set of base vectors,

$$\ket{x_1\,s_1}\otimes\ket{x_2\,s_2} = \ket{x_1\,s_1\,x_2\,s_2}$$

where the indices 1 and 2 are for the particles, $x$ is the particle position and $s$ its spin. The two particles execute on the line a discrete quantum walk $U=V(U_0\otimes U_0)$, defined by the composition of the split-step operator,

$$U_0 \ket{x\,s} = U_0 = T_\MI R(\theta_\MI) T_\PL R(\theta_\PL) \ket{x\,s}$$

which depends on the two angles $\theta_\pm$, and an interaction operator,

$$V\ket{x_1\,s_1\,x_2\,s_2} = \E^{\I \phi} \delta_{x_1,x_2} \ket{x_1\,s_1\,x_2\,s_2}.$$

which adds a phase $\phi$ to the quantum state when the two particles are at the same site.

The split-step operator rotates the particle spin,

$$R(\theta) = 1_x \otimes \exp(\I \sigma_y \theta)$$

and translates the spin-up projection one lattice step to the right,

$$T_\PL = \sum_x \left( \ket{x+1} \bra{x} \otimes \ket{0} \bra{0} + \ket{x} \bra{x} \otimes \ket{1} \bra{1} \right)\,,$$

and the spin-down projection one step left,

$$T_\MI = \sum_x \left( \ket{x} \bra{x} \otimes \ket{0} \bra{0} + \ket{x-1} \bra{x} \otimes \ket{1} \bra{1} \right)\,.$$

The interaction depends on the distance of the two particles, it breaks then the translation symmetry of the free system, but preserves the conservation of center of mass motion.

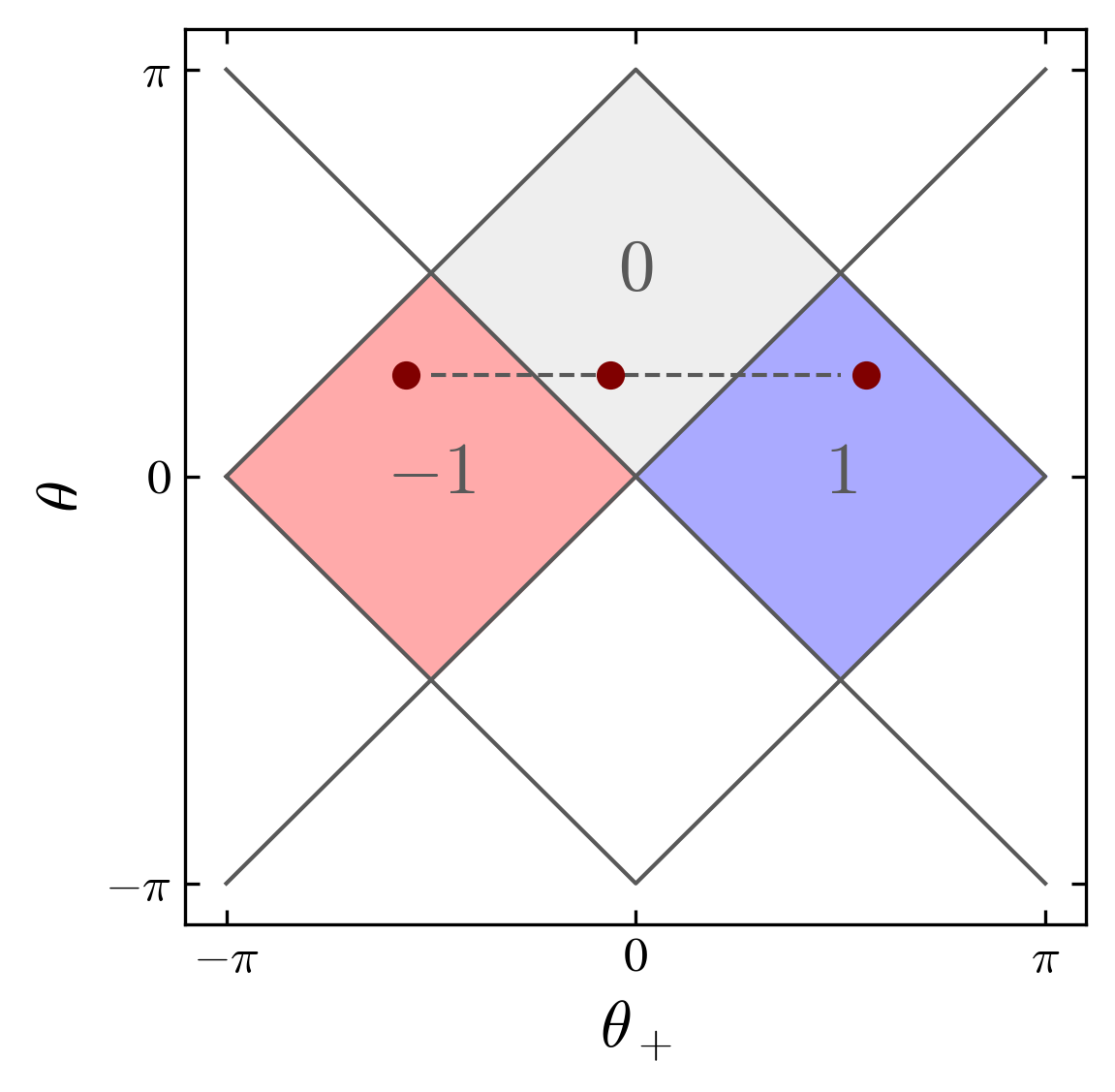
One important property of the split-step quantum walk is that its energy bands structure possesses a nontrivial topology Kitagawa et al. (2010). Depending on the choice of the two rotation angles, a topological charge $c=-1,0,1$ can be defined, as showed by Cedzich et al. (2016). We introduce in addition, an interface at $x=0$ separating a left region with topological charge $c=0,1$, and a right region with charge $c=-1,0,1$ (figure below).

Topological charge in the plane defined by the two rotation angles. The dots are the angles used in the numerical calculations: 6 different types of interfaces are possible: left $0$ or $1$, and right $-1,0,1$

We fix $\theta_\MI=\pi/4$ for $x<0$, and choose $\theta = \theta_\PL(x\ge 0)= (-\pi/3,\pi/16,3\pi/8)$ for the corresponding three charges $(-1,0,1)$ in the right region, and $\theta_+(x<0) = -\pi/16$, with charge $0$, or $\theta_+(x<0) = \pi/2+\pi/16$, with charge $1$, in the left region. The set of parameters are defined by the four labels code $(c,b,g,i)$, where:

$c = 0,1$: is the left region charge, $0$ or $1$,
$b = 0,\ldots,4$: labels the initial state, the four bell states $\{\phi_\pm,\psi_\pm\}$ with $b=0,2$ for the symmetric states and $b=1,3$ for the antisymmetric ones; $b=4$ corresponds to a separable state $\ket{0000}$,
$g = 0,\ldots,4$: labels the interaction “strength” $\phi=0,\pi/3,\pi/2,3\pi/4,\pi$, and,
$i = 0, 1, 2$: the three $x>0$ different charges, $-1,0,1$.

Band structure

We compute the spectrum of the one step operator $U$,

$$U\ket{E_n} = E_n \ket{E_n}$$

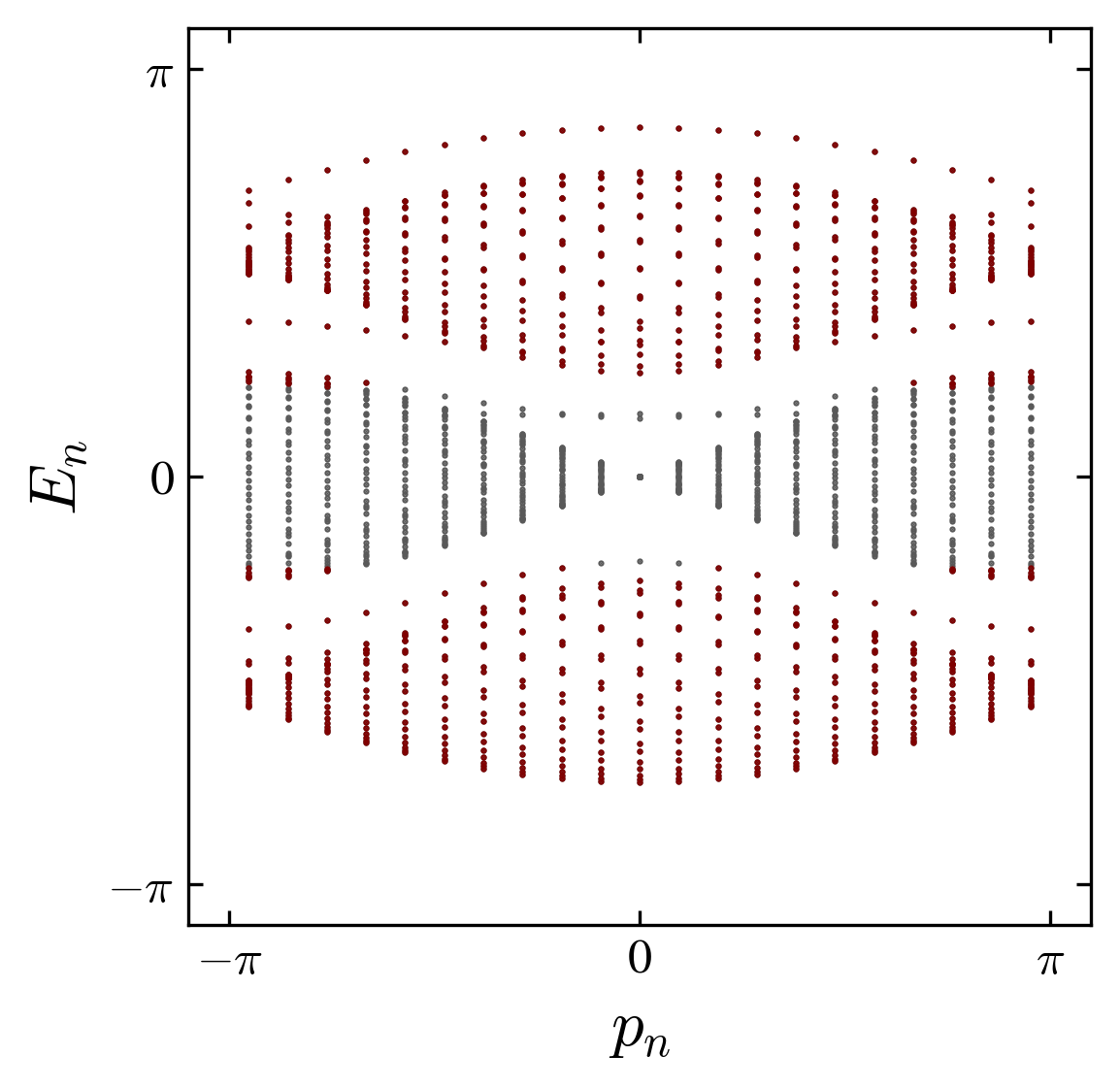
by exact diagonalization, for the homogeneous (one phase) system. For the non interacting case, we find a gapped spectrum. This structure is preserved for the interacting case with however the appearance of bound modes within the gaps (figure).

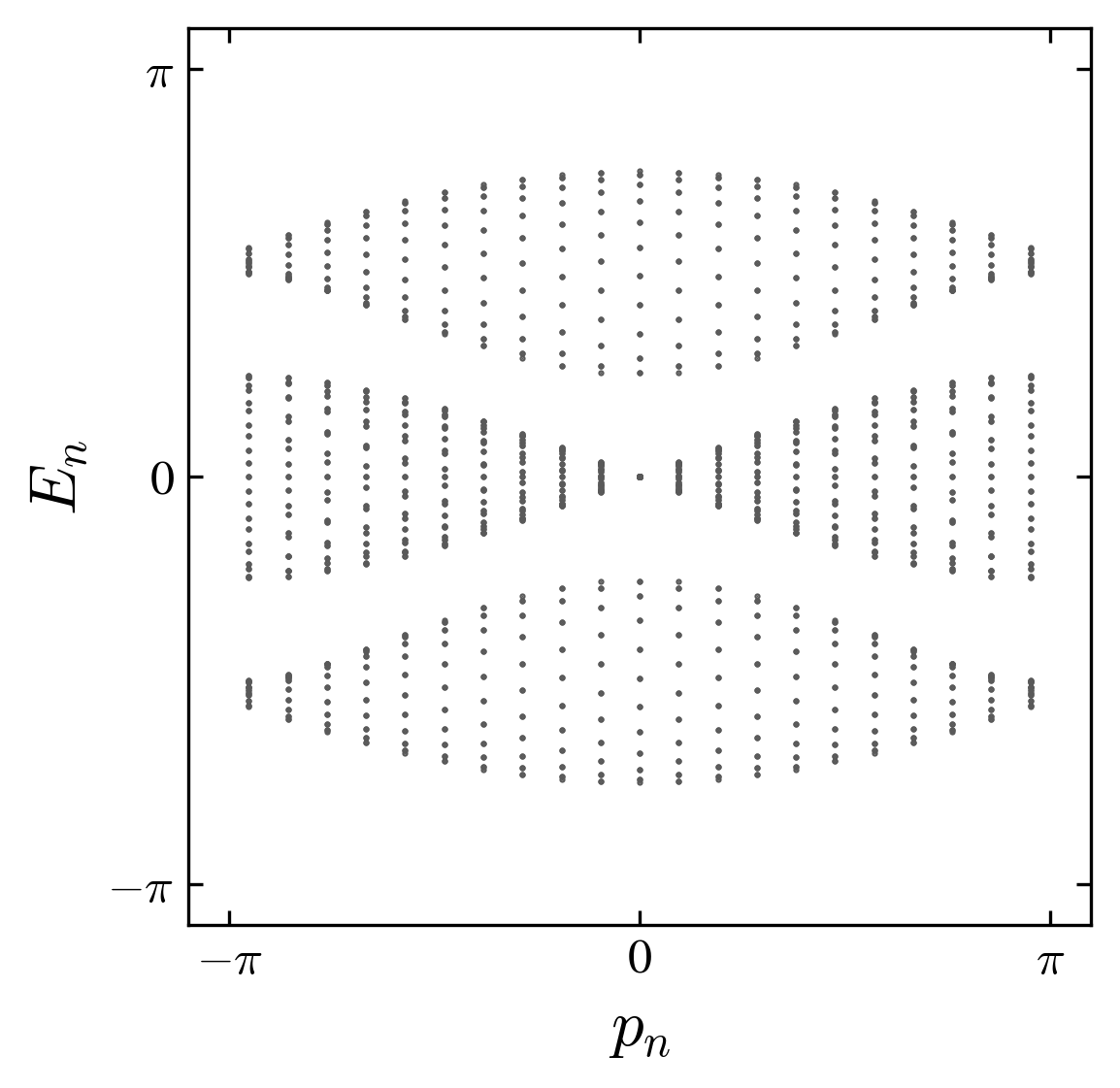
Energy bands for the non interacting case $\phi=0$ and interacting case $\phi=\pi/3$. Note the appearance of bound states within the gap, in the intearcting case. The quasienergies are ordered by the value of the momentum of the center of mass of the two particles $p_n$.

The bounded state corresponds to the binding of the two particles in a “molecular” state Ahlbrecht et al. (2012).

Phenomenology

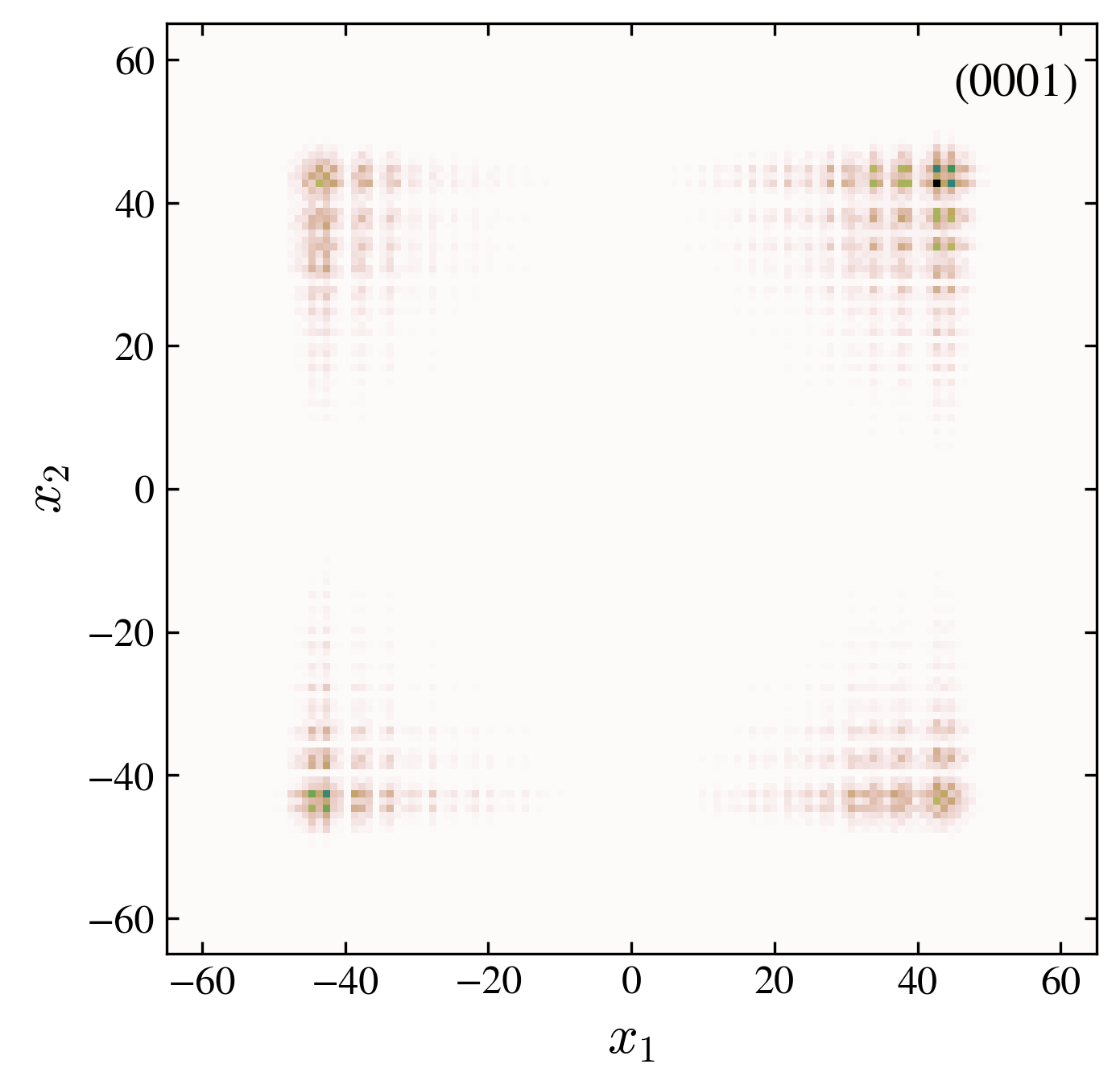
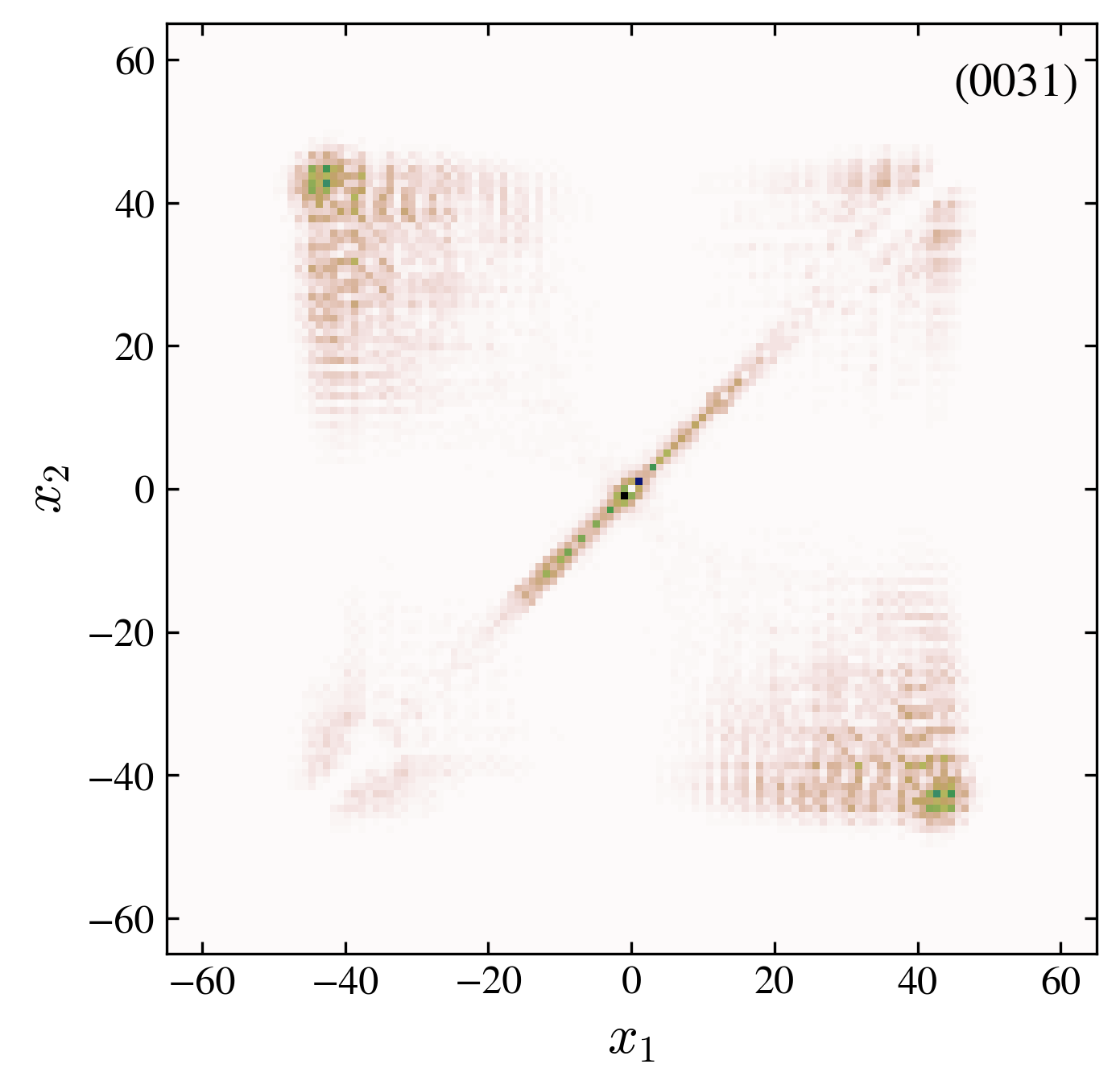
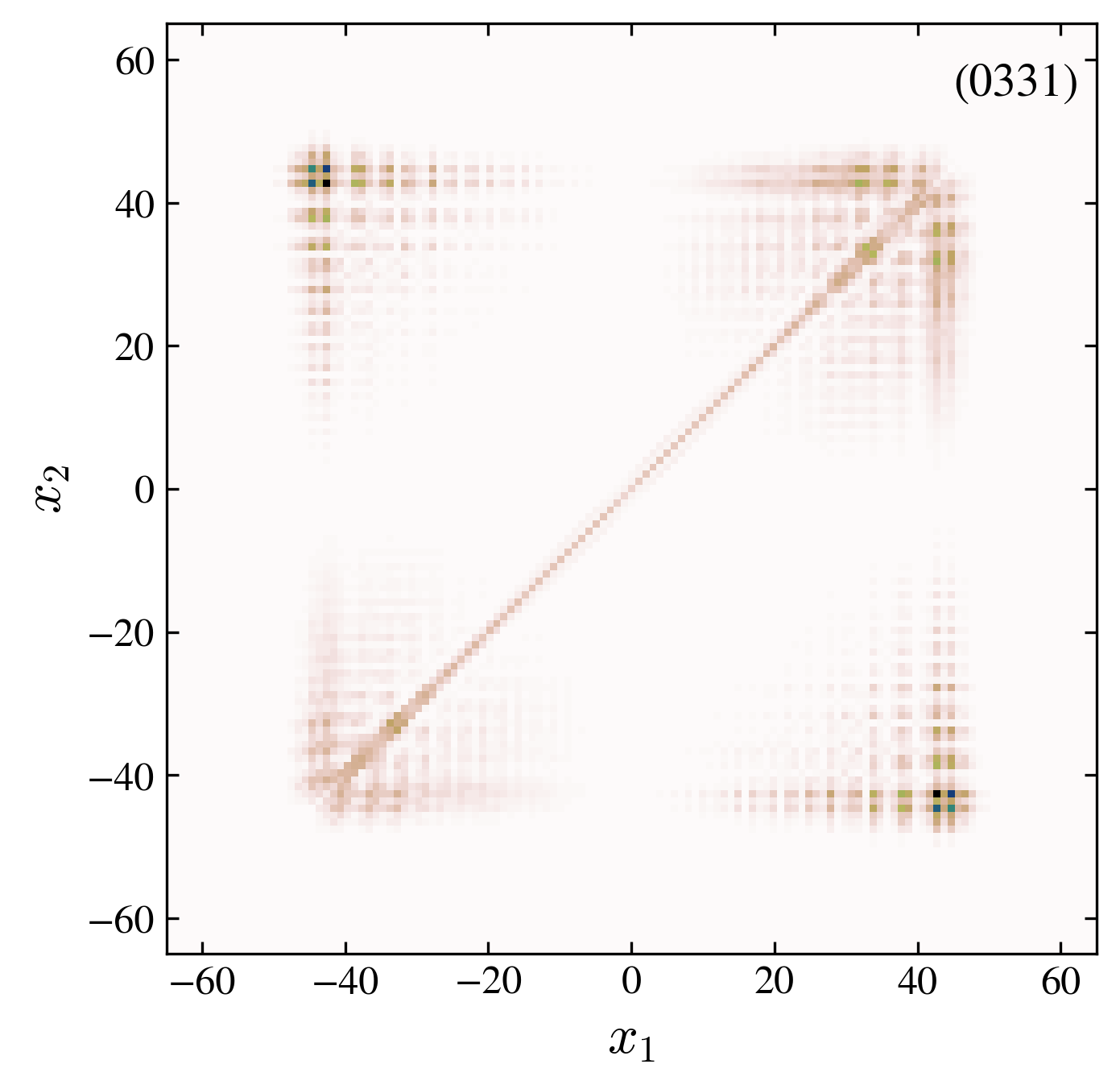
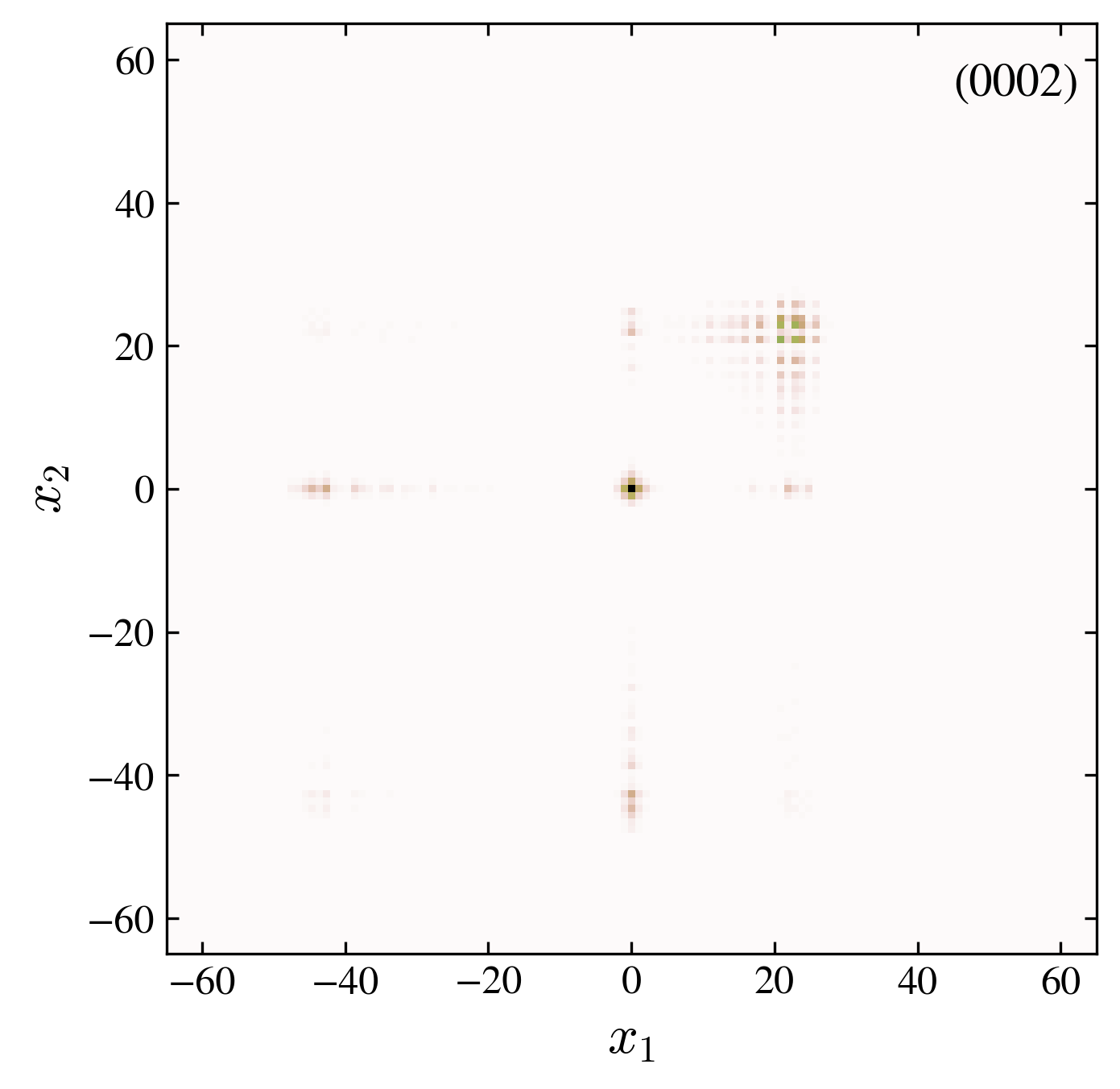
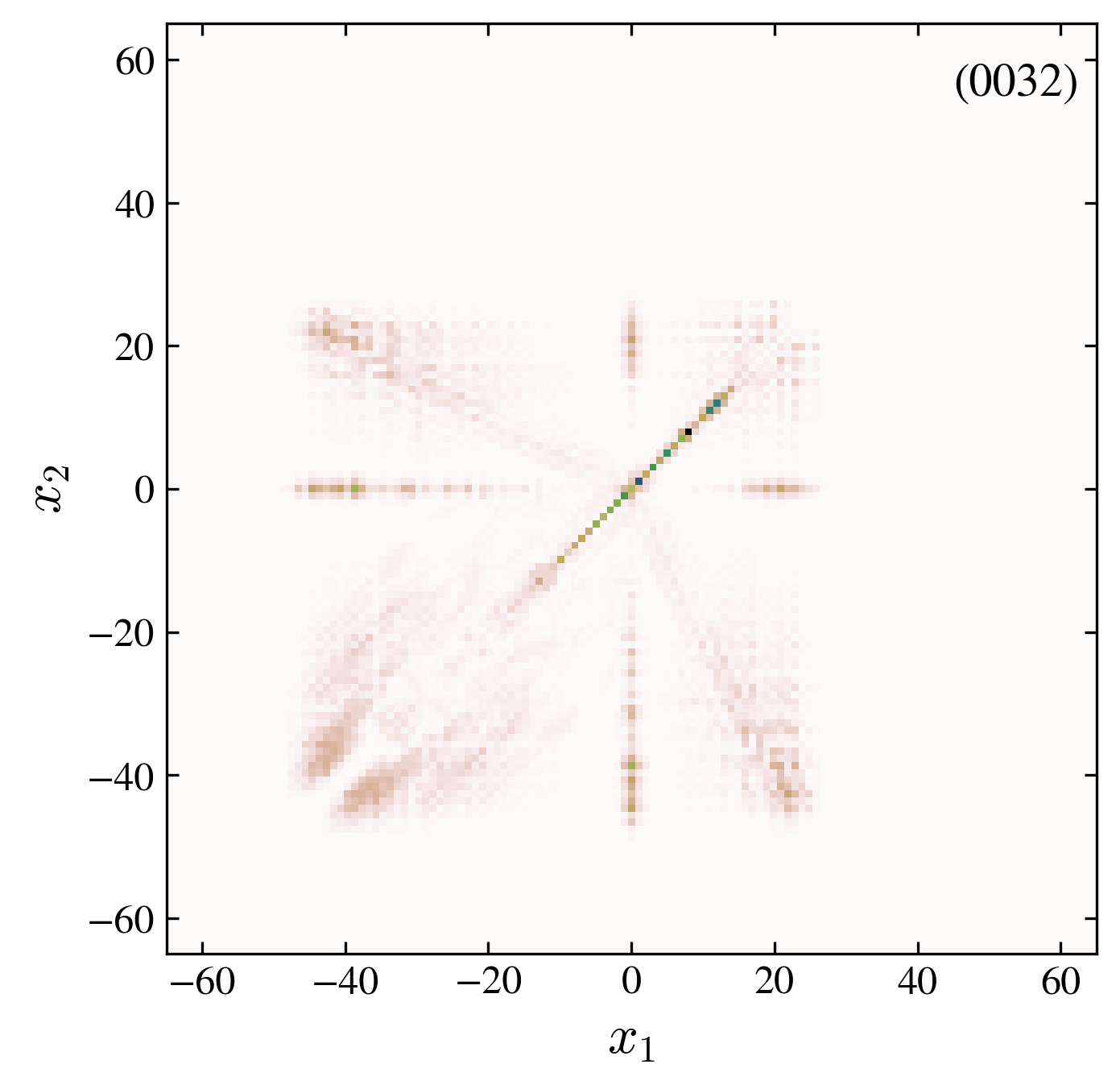
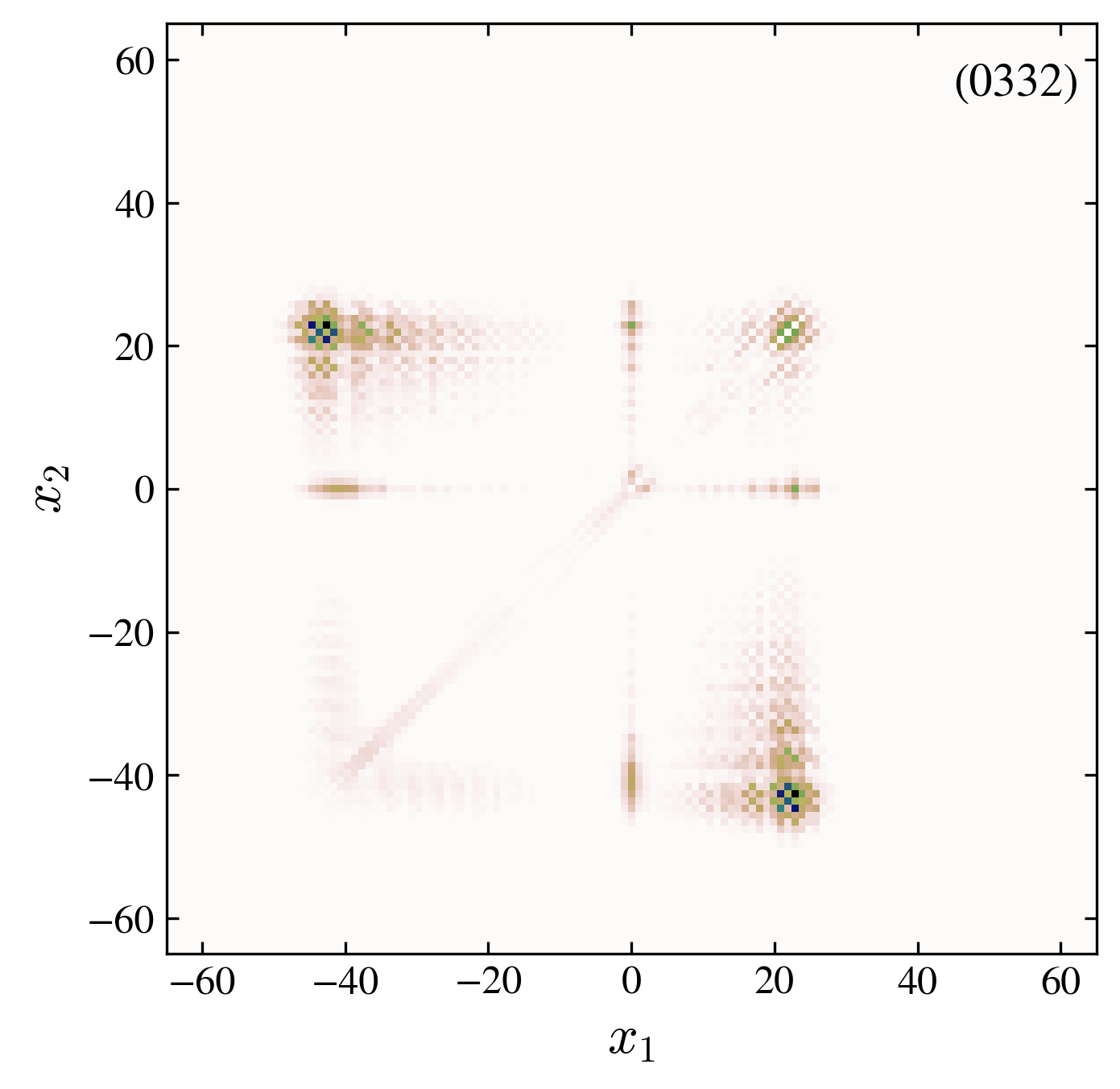
Two particles probability distribution after $60$ walk steps. We compare the free and interacting case, for symmetric and antisymmetric initial conditions (see the four label code in each pannel).

We investigate the evolution of the two particle probability $P(t)$ (images above):

“0001” free trivial case (there is no interaction or interface): the two particles spread together ballistically. This case follows the one particle quantum walk, without edge state.
“0002” free, 01-interface: the presence of a localized state contributes to a finite probability $P(t)$ to find the two particles at the origin at long times.
“0031” interaction, trivial: in a trivial topology, the interaction allows a binding of the two particles. In addition a localized state appears at the origin.
“0032” interaction, 01-interface: the addition of the edge state suppress the antisymmetric spreading, observed in the “0031” case.
“0331” interaction, trivial, antisymmetric: with an antisymmetric initial state the localization at the origin, present in the symmetric case “0031”, vanishes. However, in spite of the tendency of the two particles to avoid each other, a binding state is present.
“0332” interaction, 01-interface, antisymmetric: the interaction suppress the localized state and modifies the velocity of propagation of the probability.

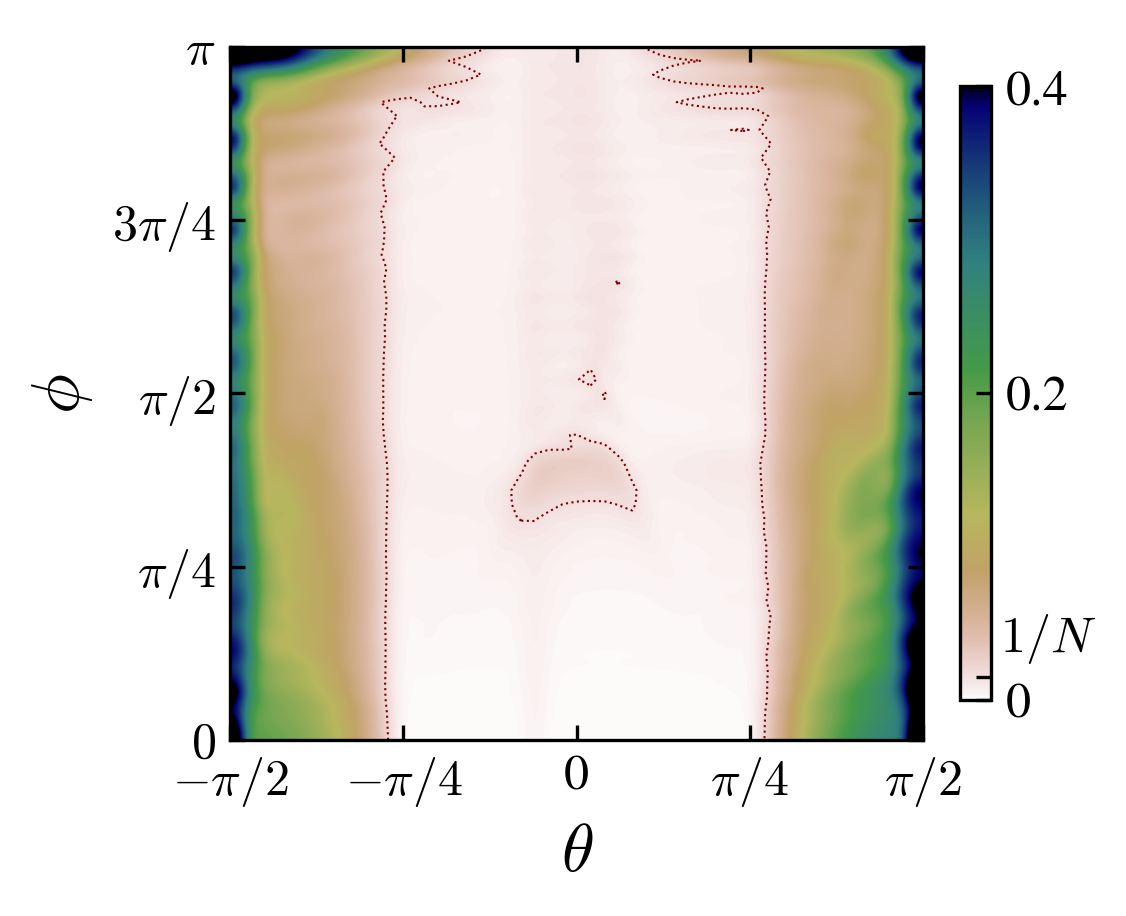
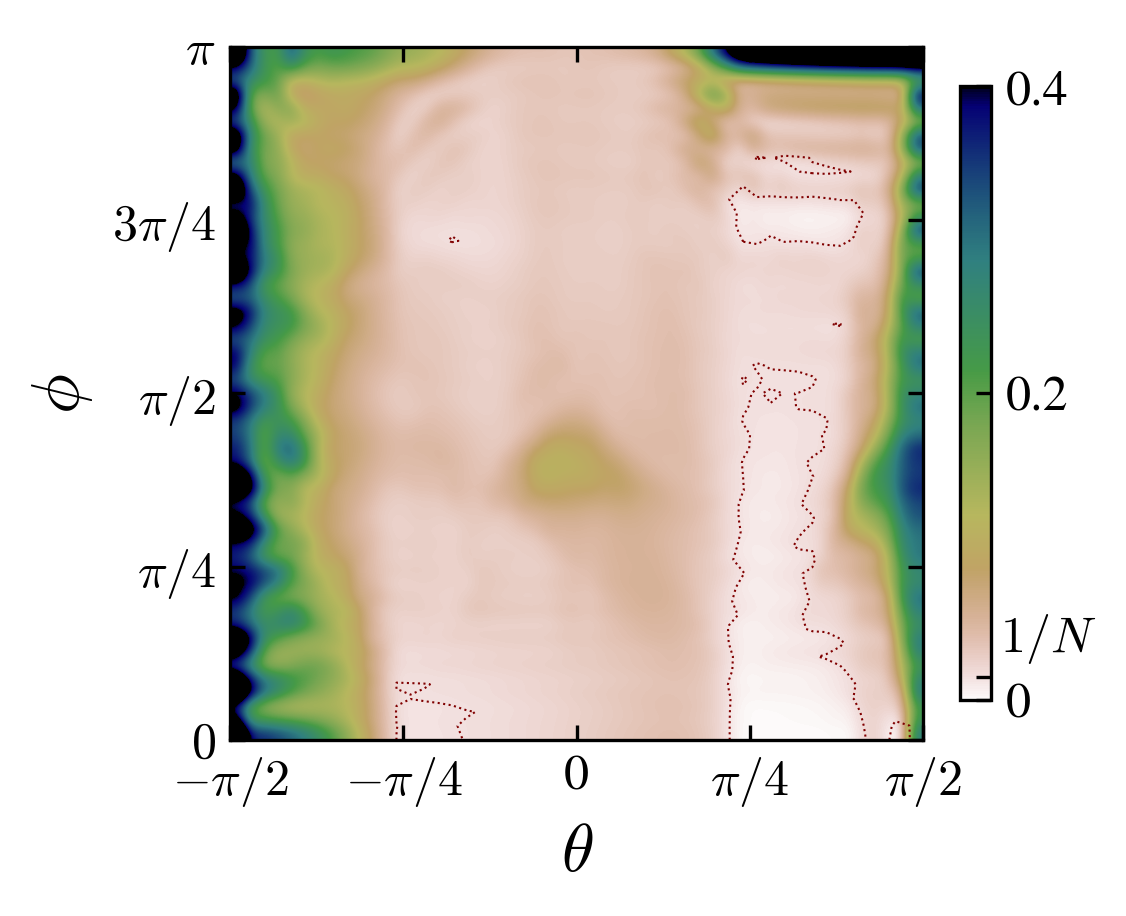
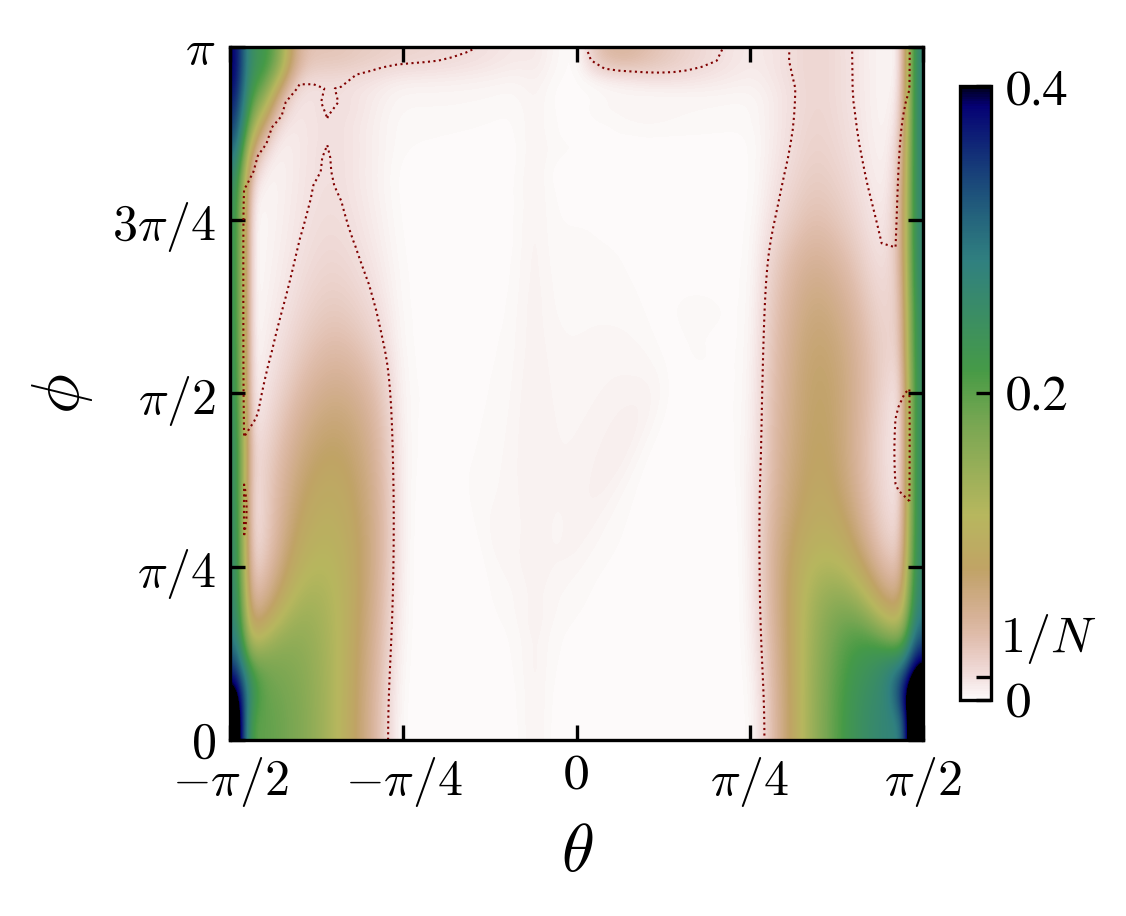
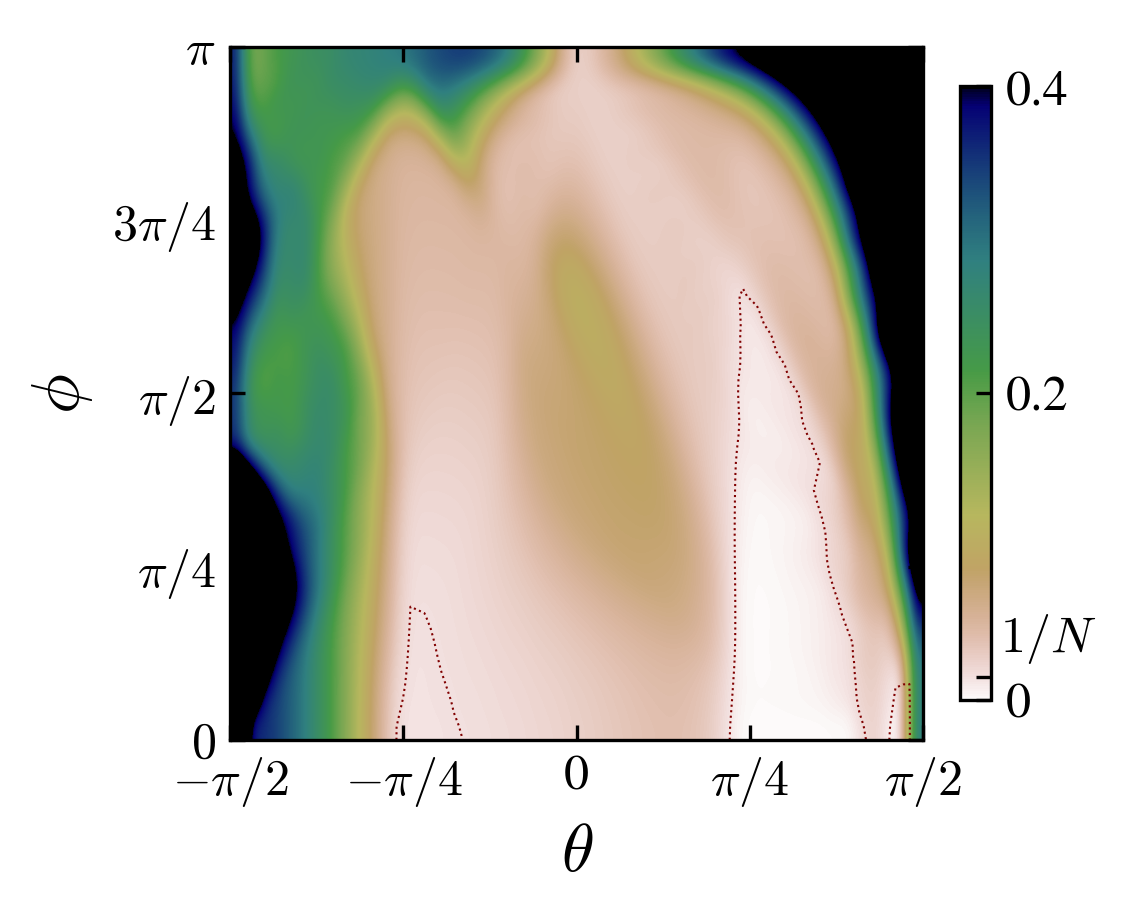
Angle-interaction phase space for left charge-initial state pairs $(cb)$: “00”, “03”, “10”, “13”. The colors are the probability at the origin, if grater than $1/N$ ($N$ is the number of steps), the state is said “localized”.

From the observation of the phase space in the rotation angle-interaction strength parameters, one notice the appearance of localization-delocalization transitions induced by the interaction (images above).

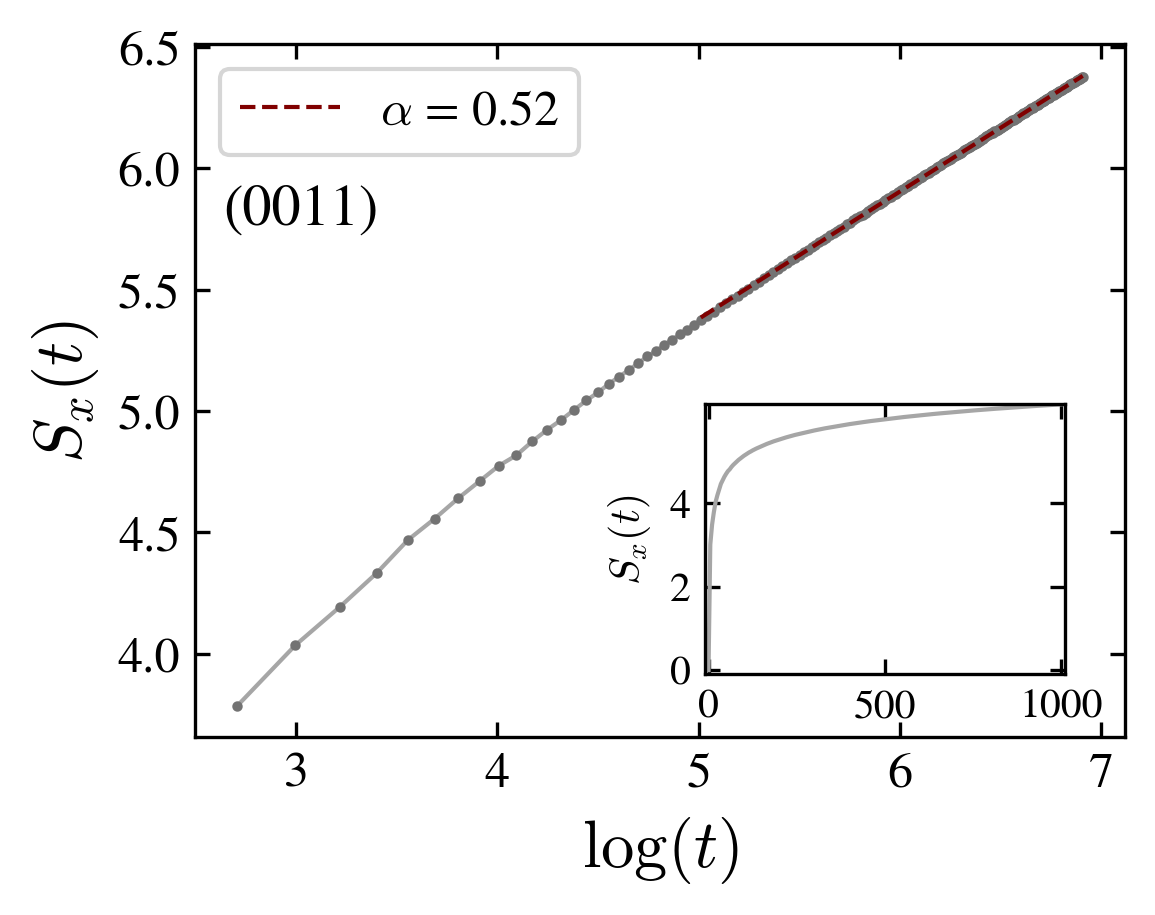
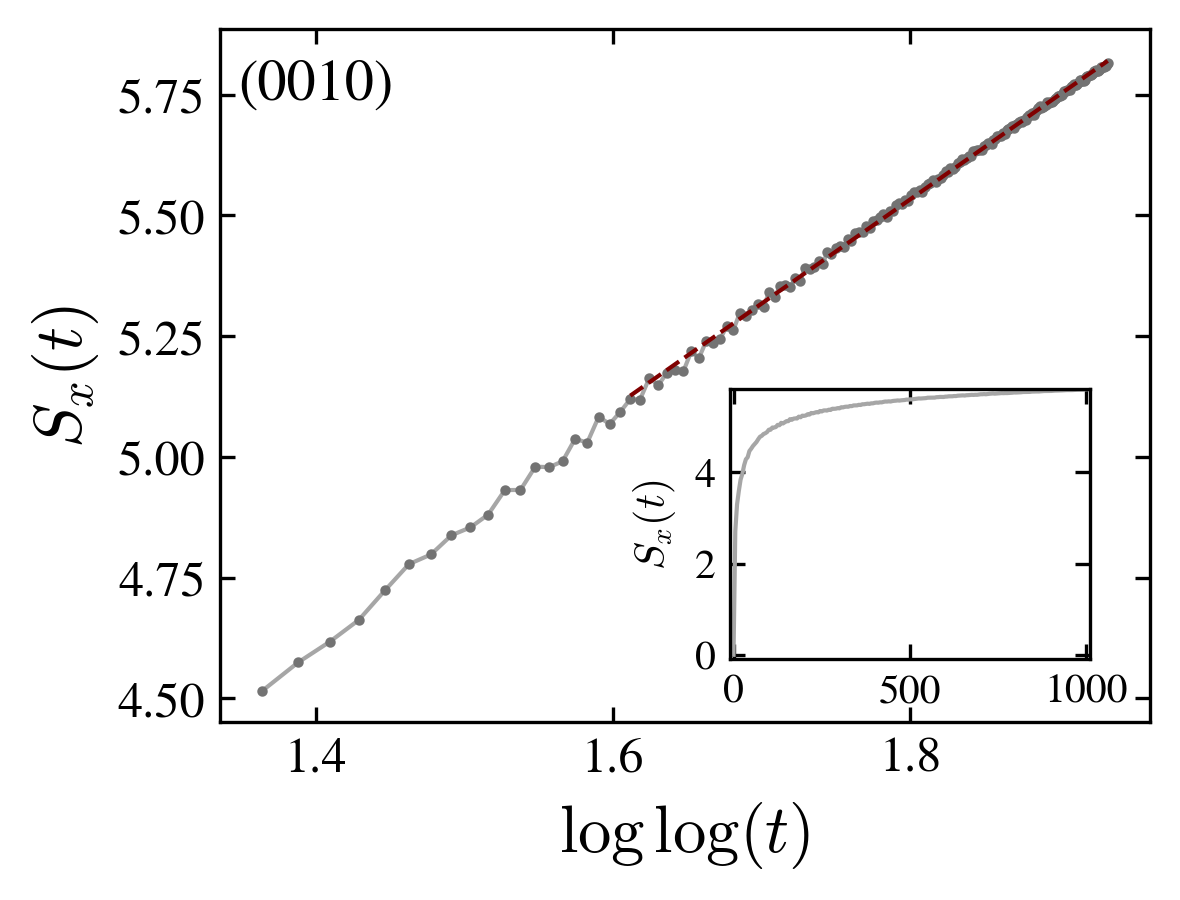
Entanglement entropy for the delocalized and localized cases: a transition between logharithmic and double logarithmic growth is observed.

The existence of localized states has a profound impact on the behavior of the entanglement entropy:

$$S_x(t) = -\mathrm{Tr}\, \rho_x(t) \log \rho_x(t),\; \rho_x(t) = \mathrm{Tr}_{\bar{x}} \rho_{x,\bar{x}}(t)$$

Indeed, in the delocalized state it grows logarithmically,

$$S_x(t) \sim \alpha \log t\,,$$

while in the localized case its growth is very slow, as an iterated logarithm,

$$S_x(t) \sim \log(\xi \log t)\,,$$

(figure above).

Discussion

We noted that the evolution of the system depends on the type of the interface; interfaces between charge $-1$ and $0$ regions, or $1$ and $0$ are not equivalent. Furthermore, the overlapping of the initial state with the edge state (for example, putting the particles on the left or on the right of the interface), will affect the details of the system’s evolution. However, basic properties like localization and binding, are observed to be robust, they do not depend on the details of the initial condition. Antisymmetric states favor delocalization of the walk, and the unbinding of the molecule. Symmetric states, on the contrary, preserve the edge states and the molecular binding.

One interesting effect of the interaction is that it can induce localized states, which are absent without interaction, even in the trivial topological state. This effect is present, for different values of the interaction strength, independently of the initial state. Moreover, the interaction can also destroy the edge states and allows the propagation of the information between regions with different topology. Therefore, the interaction can be used as a control parameter of the information transport.

The molecular states, which can propagate along the line, compete with the localized state, which tends to sticks the particles at the interface. Depending on the phase of of the interaction, a delocalization is possible. For the particular value $\phi=\pi$, strongly localized states are observed. For intermediate values, in the range $\phi=(\pi/3,\pi/2)$, localized states in the free delocalized region appear, for symmetric states, but also for antisymmetric states depending on the topology.

We measured the entanglement entropy of one particle and found that it steadily increases over time. However, at variance with other interacting systems, its growth is not simply proportional to time, but shows two different regimes according to the localization of the walk. For delocalized states the entropy growths logarithmically, while for localized states it growths as a doubly iterated logarithm.