Random physics

Alberto Verga, research notebook

\(\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}[1]{\boldsymbol{#1}}\)

Work in progress! This lecture is intended for students of the “Licence de physique”, and in particular to those interested in theoretical physics.

L’information quantique : du qubit a l’intrication

En informatique, quand on parle d’information on se réfère essentiellement à la théorie de Shannon. En effet, Shannon définit une mesure de la quantité d’information d’un message en unités du bit. Il partit du fait qu’un message peut être codé par un alphabet de deux symboles 0 et 1, ce qui correspond précisément à \(1\, \mathrm{bit}\) d’information. Par conséquent, un message de \(N\) caractères, donc un message parmi \(2^N\) possibles, contiendrait \(N\) bits d’information :

$$N = \log\big(2^N\big)$$

(où on note \(\log\) le logarithme de base 2) puisqu’en principe il faut préciser les les \(N\,\mathrm{bit}\) pour reproduire le message. L’idée de Shannon est de considérer un message comme étant un élément d’un ensemble, auquel on attribue une probabilité. Cet exemple nous permet de comprendre que la quantité d’information serait quelque chose comme le logarithme de la taille de l’ensemble de messages exprimée en bits. Cette intuition est juste pourvu que les symboles du message puissent être considérés comme n’ayant aucune corrélation. Le cas extrême d’un message de longueur \(N\) constitué exclusivement de 0, ne contiendrait pas plus d’information que s’il avait une longueur de \(2N\). Pour tenir compte des corrélations entre les symboles d’un message, Shannon introduisit la notion de distribution de probabilité \(p_n\) associée a l’ensemble de messages \(n=1,2,\ldots, 2^N\). Il démontra que la quantité d’information est donnée par la formule

$$S = - \sum_n p_n \log p_n$$

qu’on appelle l’entropie de Shannon (1948). C’est un fait remarquable que Gibbs (1902) arriva à une formule équivalente en physique statistique, pour l’entropie thermodynamique, en assignant une distribution de probabilité aux configurations d’un système constitué d’un grand nombre de particules.

Exercice Montrez que l’entropie de Shannon pour une distribution uniforme coïncide avec le résultat précédent : \(S = N \, \mathrm{bit}\).

Exercice Considérez un ensemble de messages écrits avec quatre symboles \(1,2,3,4\); la fréquence des \(1\) est \(p_1=1/2\), celle des \(2\), \(p_2 = 1/4\), et celle des \(3\) et \(4\), \(p_3 =p_4 = 1/8\). Si pour coder ces messages on utilise deux bits \(00, 01, 10, 11\), montrez que la longueur typique d’un message est de \(2\,\mathrm{bit}\) par caractère. Par contre, si l’on code les messages avec un bit pour le 1, \(0\), 2 bits pour le 2, \(10\), et trois bits pour 3 et 4, \(110\) et \(111\), montrez que la longueur est de \(7/4\) par caractère. Calculez l’entropie de Shannon et comparez avec les résultats précédents.

Solution \((1/2+1/4+1/8+1/8) \times 2 \, \mathrm{bit} = 2 \, \mathrm{bit}\) et \(1/2 \times 1 + 1/4 \times 2 + 1/8 \times 3 + 1/8 \times 3 \, \mathrm{bit} = 7/4 \, \mathrm{bit}\). (On utilise “bit” pour l’unité, comme toute autre unité elle est invariable.)

La notion mathématique d’unité d’information (le bit, comme l’information, est une grandeur adimensionnelle) peut être réalisée physiquement par un quelconque système ayant deux phases stables, comme un aimant dont l’aimantation peut pointer vers deux directions opposées, et dont le changement de direction ne peut pas s’effectuer spontanément. C’est le principe d’une mémoire magnétique. Un autre exemple est celui du transistor, lequel peut passer d’un état conducteur vers un état isolant, selon la tension appliquée.

En mécanique quantique l’information apparaît naturellement comme étant une propriété physique. Elle est intimement associée à l’état quantique. Il nous faut donc étudier ce qu’est qu’un état quantique. On commence par le système le plus simple possible : le qubit.

Pause mathématique : l’espace de hilbert

L’espace de hilbert \(\mathcal{H}\) à deux dimensions est l’espace vectoriel complexe \(\mathbb{C}^2\). Il est la généralisation des vecteurs de \(\mathbb{R}^2\) avec des coefficients complexes. On note les éléments \(\mathcal{H}\) avec des kets

$$\ket{\psi} \in \mathcal{H},$$

ils sont constitués d’une étiquette, ici \(\psi\), laquelle évoque la grandeur physique décrite par l’état, et du symbole \(|\cdots\rangle\). La généralisation à la dimension \(N\) est immédiate \(\mathcal{H} \sim \mathbb{C}^N\).

À chaque ket \(\ket{\psi}\) on associe un bra, \(\bra{\psi}\), tel que leur produit nous donne la norme du vecteur :

$$\braket{\psi|\psi} = \big| \ket{\psi} \big|^2,$$

ou plus généralement, on peut former le produit des deux kets quelconques, appelé braket,

$$\braket{\phi|\psi} = \braket{\psi|\phi}^\star \in \mathbb{C}.$$

Il s’agit donc de la généralisation du produit scalaire des vecteurs réels. Le bra \(\bra{\psi}\) associé au ket \(\ket{\psi} \in \mathcal{H}\) appartient à l’espace dual \(\mathcal{H}^\dagger\), obtenu par transposition et conjugaison de l’espace \(\mathcal{H}\):

$$\bra{\psi} = (\ket{\psi}^\star)^T = (\ket{\psi})^\dagger$$

avec \(\star\) la conjugaison, \(T\) la transposition, et \(\dagger\) leur combinaison.

Une base orthonormale \(\ket{n}\) d’un espace à deux dimensions est constituée de deux vecteurs \(n=0,1\); elle peut être représentée par les vecteurs colonne de la base canonique :

$$\ket{0} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \ket{1} = \begin{pmatrix} 0 \\ 1 \end{pmatrix},$$

où

$$\braket{0|0} = \braket{1|1} = 1, \quad \braket{0|1} = 0.$$

Les bras \(\bra{0}\) et \(\bra{1}\) sont donc les vecteurs ligne :

$$\bra {0} = \begin{pmatrix} 1 & 0 \end{pmatrix}, \quad \bra{1} = \begin{pmatrix} 0 & 1 \end{pmatrix}.$$

Tout vecteur de \(\mathcal{H}\) bi-dimensionnel peut s’écrire comme la superposition des deux vecteurs de la base :

$$\ket{\psi} = a \ket{0} + b \ket{1} = \begin{pmatrix} a \\ b \end{pmatrix}, \quad |a|^2 + |b|^2 = 1,$$

où on a supposé que la norme de \(\ket{\psi}\) est 1. Les “coordonnées” du \(\ket{\psi}\) s’obtiennent par produit scalaire avec les vecteurs de la base :

$$\braket{0|\psi} = a, \quad \braket{1|\psi} = b.$$

Notez que le bra correspondant est

$$\bra{\psi} = a^\star \bra{0} + b^\star \bra{1}.$$

Dans le cas de dimension \(N\) on aurait :

$$\ket{\psi} = \sum_{n=1}^{N} \psi_n \ket{n}$$

avec \(\{\ket{n}\}\) la base canonique de dimension \(N\):

$$\braket{n|m} = \delta_{nm}$$

où \(\delta\) est la “delta” de kronecker, \(\delta_{nn} = 1\) et \(\delta_{nm} = 0\) pour \(n \ne m\).

Les applications linéaires sur l’espace de hilbert sont les opérateurs, ils transforment un vecteur de \(\mathcal{H}\) dans un autre vecteur du même espace :

$$\ket{\phi} = O \ket{\psi}$$

avec \(O\) un opérateur et \(\ket{\psi}, \ket{\phi} \in \mathcal{H}\). Le transposé et conjugué \(O^\dagger = O^{\star T}\) est l’adjoint de \(O\). La composition d’opérateurs est aussi un opérateur.

On représente les opérateurs à l’aide de matrices de nombres complexes, dans une base donnée. Par exemple si la base est \(\ket{n}\), la base canonique de \(\mathcal{H}\)

$$\braket{n | O | m} = O_{nm}$$

est l’élément de matrice de la ligne \(n\) et de la colonne \(m\).

  • un opérateur \(O\) est hermitien si \(O^\dagger = O\),
  • un opérateur \(U\) est unitaire si \(U^\dagger U = 1\) (avec 1 la matrice unité),
  • un opérateur \(P\) qui satisfait \(P^2 = P\) est un projecteur.

L’équation des valeurs propres d’un opérateur hermitien \(O\) est

$$O \ket{n} = o_n \ket{n}$$

où \(\ket{n}\) est le vecteur propre de valeur propre réel \(o_n\). Évidemment, dans la base de vecteurs propres de \(O\), sa matrice associée est diagonale : \(O_{nm} = o_n \delta_{nm}\).

Par exemple les matrices de Pauli,

$$X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}, \quad Y = \begin{pmatrix} 0 & -\I \\ \I & 0 \end{pmatrix}, \quad Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},$$

sont à la fois hermitiennes et unitaires EX.

Les matrices de pauli sont de trace nulle et de déterminant \(1\). Les valeurs propres des ces trois matrices sont \(\{1,-1\}\); par exemple

$$X \ket{+} = \ket{+}, \quad \ket{+} = \frac{1}{\sqrt{2}} \begin{pmatrix}1 \\ 1 \end{pmatrix}$$

et

$$X \ket{-} = -\ket{-}, \quad \ket{-} = \frac{1}{\sqrt{2}} \begin{pmatrix}1 \\ -1 \end{pmatrix}$$

avec \(\ket{+}\) le vecteur propre de valeur propre \(1\) et \(\ket{-}\) celui de valeur propre \(-1\); notez que \(\braket{+|-} = 0\) et qu’ils sont normalisés : ils forment donc une base de \(\mathcal{H}\) (espace de hilbert à deux dimensions).

L’opérateur \(P = \ket{0} \bra{0}\) est un projecteur :

$$P^2 = (\ket{0} \bra{0}) (\ket{0} \bra{0}) = \ket{0} \braket{0|0} \bra{0} = \ket{0} \bra{0} = P.$$

appliqué aux éléments de la base, on obtient

$$P \ket{0} = \ket{0}, \quad P \ket{1} = 0.$$

Le produit de kronecker \(\otimes\) de deux matrices \(A\) de dimensions \(n \times m\) et \(B\), de dimension \(n' \times m'\) est une autre matrice \(C\) de dimension \(nn' \times mm'\): \(C_{n'i+j,m'k+l} = A_{ij} B_{kl}\). Par exemple

$$X \otimes Z = \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \\ 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & Z \\ Z & 0 \end{pmatrix}$$

où on a utilisé l’écriture d’une matrice par blocs. Le produit de kronecker n’est pas commutatif \(A \otimes B \ne B \otimes A\). En outre, une propriété importante est

$$(A \otimes B) (C \otimes D) = (AC) \otimes (BD)$$

avec \(A,C\) deux matrices appartenant au premier espace et \(B,D\) au deuxième.

Principes de la mécanique quantique

  • L’état quantique est un ket de norme 1, appartenant à un espace de hilbert
    $$\ket{\psi} \in \mathcal{H}, \quad \braket{\psi | \psi} = 1.$$
  • Les grandeurs physiques, ou observables, sont des opérateurs hermitiens :
    $$O \ket{n} = o_n \ket{n}, \quad o_n \in \mathbb{R}, \; \braket{n|m} = \delta_{nm}.$$
  • La valeur espérée d’une observable \(O\) dans état \(\ket{\psi}\) est \(\braket{O} = \braket{\psi | O | \psi}\).
  • Les résultats de la mesure d’une observable \(O\) sont ses valuers propres \(o_n\). La probabilité de trouver \(o_n\) est
    $$p(n) = \big| \braket{n|\psi} \big|^2$$
    si l’état de système est \(\ket{\psi}\).
  • La transformation entre deux états d’un système est un opérateur unitaire.
    $$\ket{\phi} = U \ket{\psi}, \quad \braket{\phi|\phi} = \braket{\psi|\psi} = 1.$$
  • L’espace de hilbert d’un système composite est le produit de kronecker des espaces de chaque système.

Mach-Zehnder

Interféromètre de Mach-Zehnder, avec un déphasage \(\delta\) entre les deux chemins. Il est composé de deux lames semi-transparentes et de deux miroirs. \(D\) et \(D'\) détectent le photon initial \(\ket{0}\). \(r\) et \(t\) sont les amplitudes de réflexion et de transmission, que l’on suppose telles que \(|r|^2 = |t|^2 = 1/2\).

Pour illustrer ces principes analysons le comportement d’un photon. Le “principe de superposition”, le fait que les états sont des vecteurs “complexes”, traduit les observations expérimentales, comme celle de l’interférence à un photon. Le photon est le quantum de lumière. Il a été postulé au début du XXème siècle pour expliquer le rayonnement du corps noir (Planck 1900) et l’effet photoélectrique (Einstein 1905). Quand on fait passer un photon à travers une lame semi-transparente on le détecte toujours sur un détecteur, soit qu’il a été réfléchi ou qu’il a été transmis, mais jamais simultanément sur les deux détecteurs (placés sur les deux chemins possibles). Si maintenant on le fait passer par deux lames, comme dans la figure de l’interféromètre de Mach-Zehnder, le résultat est surprenant : le photon interfère avec “lui-même”, il se comporte comme s’il avait “emprunté” les deux chemins avant d’arriver au détecteur. Notez que ces phrases n’ont pas beaucoup de sens, du point de vue de la sémantique elles sont même contradictoires : pour “expliquer” le phénomène mesuré au laboratoire on doit appliquer les principes de la mécanique quantique.

Il s’agit donc d’un système quantique avec deux états, transmis ou réfléchi, \(\ket{0}\) et \(\ket{1}\). L’expérience avec une lame nous montre qu’en fait \(0\) est un état arbitraire, mais il doit être orthogonal à celui réfléchi (\(\braket{0|1} = 0\)). On suppose maintenant, que la transmission ne change pas l’état, mais introduit une amplitude \(t=1/\sqrt{2}\), tandis que la réflexion change l’état et introduit un déphasage, \(r = \I/\sqrt{2}\). On respecte bien que \(|r|^2+|t|^2=1\) (d’où les racines carrées de 2). Supposons que l’état initial est \(\ket{0}\), en suivant le chemin dans l’appareil on a les transformations suivantes EX

$$\ket{0} \xrightarrow{\text{lame 1}} t \ket{0} + r \ket{1} \xrightarrow{\text{lame 2}} t(t\ket{0} + r\ket{1}) + r(r\ket{0} + t\ket{1}) = \I \ket{1} = \ket{\psi}.$$

Nous déduisons que la probabilité d’observer le photon initialement dans l’état \(0\), sur le détecteur \(D\),

$$p_0(1) = \big| \braket{1 | \psi} \big|^2 = 1$$

est 1, et donc zéro la probabilité de le détecter en \(D'\). Notez que les chemins qui mènent à \(D\) ont une réflexion (\(rt\) ou \(tr\)), tandis que ceux qui mènent à \(D'\) n’ont pas eu ou en ont eu deux réflexions (\(tt\), ou \(rr\)).

En conclusion, l’application du principe de superposition (le fait que l’état du photon après passage à travers la lame soit une superposition de “réfléchi” et “transmis”), en conjonction avec des transformations unitaires (qui, par conséquent, conservent la probabilité) conduisent naturellement (selon les lois de la nature !) au résultat d’interférence : l’amplitude de probabilité d’un photon deux fois réfléchi ou deux fois transmis, s’annule nous donnant une probabilité 1 de le détecter en \(D\).

Si on ajoute le déphasage \(\delta\), le même calcul conduit au résultat EX

$$p_0(1) = \big| \braket{1|\psi} \big|^2 = \cos^2(\delta/2).$$

La transformation réalisée par l’action de la lame semi-transparente sur l’état du photon peut être formalisée par l’opérateur unitaire :

$$B = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & \I \\ \I & 1 \end{pmatrix}.$$

En effet, cet opérateur realise la transformation \(\ket{0} \rightarrow t \ket{0} + r \ket{1}\):

$$B \ket{0} = \frac{\ket{0} + \I \ket{1}}{\sqrt{2}}.$$

À l’aide de \(B\) le résultat précédent s’obtient par

$$\ket{\text{out}} = BB \ket{0} = \I \ket{1} = \ket{\psi}.$$

Maintenant, si nous ajoutons comme avant, un déphasage \(\delta\), on constate qu’il peut être représenté par l’opérateur (toujours unitaire)

$$S=\begin{pmatrix} 1 & 0 \\ 0 & \E^{\I \delta} \end{pmatrix}$$

l’interféromètre et simplement décrit par l’action de l’opérateur \(BSB\) EX:

$$\ket{\psi} = B S B \ket{0} = \frac{\I \E^{\I\delta/2}}{2} \big( -\sin(\delta/2) \ket{0} + \cos(\delta/2) \ket{1} \big).$$

Par conséquent, la probabilité d’observer le photon dans l’état \(1\) (en \(D\)) est

$$p_0(1) = \big| \braket{1 | \psi} \big|^2 = \cos^2(\delta/2),$$

et

$$p_0(0) = \big| \braket{0 | \psi} \big|^2 = \sin^2(\delta/2),$$

(en \(D'\)), quand \(\delta = 0\) on retrouve bien le résultat précédent.

Exercice Montrez que \(B = \E^{\I \pi X/4}\): elle représente une rotation autour de l’axe \(x\) et d’angle \(\pi/2\).

Le qubit

On appelle qubit l’état quantique d’un système physique dont l’espace de hilbert est bi-dimensionnel. L’exemple typique est celui d’un spin \(1/2\), comme celui de l’électron, mais aussi la polarisation du photon, ou deux niveaux d’énergie d’un atome qu’on contrôle à l’aide des lasers, ou enfin la charge d’une jonction de Josephson supraconductrice.

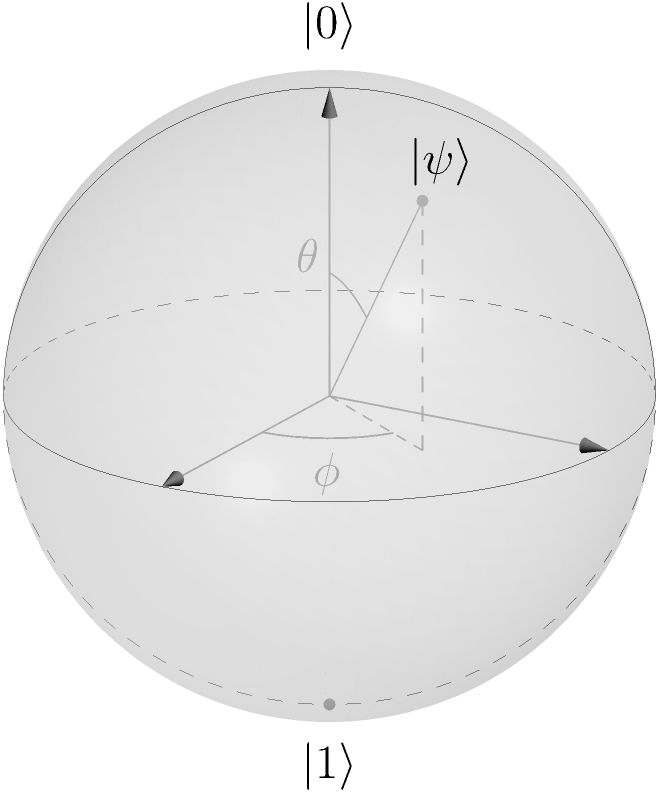
sphère de bloch

Sphère de Bloch : chaque point \((\theta, \varphi)\) de sa surface représente l’état d’un quibit ; tout état peut s’écrire comme la superposition des états \(\ket{0}\) (\(\theta = 0\)) et \(\ket{1}\) (\(\theta = \pi\)).

L’espace des états d’un qubit, est l’espace de hilbert bi-dimensionnel ; comme tout état \(\ket{\psi}\) est de norme 1, et il ne change pas si on le multiplie par une phase totale (\(\ket{\psi}\) et \(\E^{\I \alpha} \ket{\psi}\) sont le même état, quelque soit \(\alpha \in \mathbb{R}\)), le nombre de paramètres nécessaires pour le représenter se réduit à 2 : les deux angles \((\theta, \varphi)\) qui déterminent l’orientation du “vecteur” autour de la sphère unité,

$$\ket{\psi} = \cos(\theta/2) \ket{0} + \sin(\theta/2) \E^{\I \varphi} \ket{1}$$

Exercice Calculez les composantes du vecteur \(\bm n = \braket{\psi| \bm \sigma | \psi} = \big( \braket{X}, \braket{Y}, \braket{Z} \big)\).

L’état d’un qubit peut être modifié par l’application d’opérateurs unitaires, comme par exemple les matrices de pauli, que dans le contexte de l’information quantique on appelle gates (ou portes logiques). Nous avons donné un exemple avec l’interféromètre, lequel pouvait se décrire par un opérateur unitaire \(U = BSB\); cette suite des transformations unitaires d’un état “input” dans un état “output” peut se traduire dans le langage des circuits quantiques

circuit MZ

ici l’input est \(\ket{0}\) et l’output est \(\ket{\psi}\). Géométriquement, les transformations unitaires d’un qubit correspondent à des réflexions et rotations dans la sphère de bloch. Par conséquent la transformation la plus générale d’un qubit peut se décomposer essentiellement en trois rotations (à une phase multiplicative près), par exemple en utilisant les angles d’Euler (le curieux peut regarder le site angles d’Euler).

Deux qubits : intrication

L’espace de hilbert de deux qubits \(\mathcal{H}\) est le produit de kronecker des espaces de hilbert d’un qubit \(\mathcal{H}_1\); sa dimensions est donc \(2^2 = 4\). Un état de \(\mathcal{H}\) s’écrit

$$\ket{\psi} = \sum_{n,m = 0,1} \psi_{nm} \ket{n} \otimes \ket{m} = \psi_{00} \ket{00} + \psi_{01} \ket{01} + \psi_{10} \ket{10} + \psi_{11} \ket{11} \in \mathcal{H} = \mathcal{H}_1 \otimes \mathcal{H}_1$$

où on a utilisé le raccourci \(\ket{nm} = \ket{n} \otimes \ket{m}\) pour désigner les quatre vecteurs de la base, numérotés avec les chiffres binaires \(\{00, 01, 10, 11\}\).

Voyons deux exemples de circuit quantique sur deux qubits : dans le premier exemple on applique sur chaque qubit indépendamment la porte de Hadamard

$$\mathsf{H} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix},$$

(désormais on désigne les gates par de caractères sans sérif), notez que la trace de \(\mathsf{H}\) est nulle (elle peut s’écrire \(\mathsf{H} = (X+Z)/\sqrt{2}\)), mais son déterminant est \(-1\); comme les matrices de pauli elle est hermitienne et unitaire (elle est sa propre inverse \(\mathsf{H}^2=1_2\)):

circuit H

Notre deuxième exemple applique aux deux qubits, initialement dans l’état \(\ket{00}\), la porte controlled not

$$\mathsf{CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}$$

cette porte agit comme l’unité si le premier qubit est \(0\) et elle inverse le deuxième qubit si le premier est \(1\).

circuit bell

où

$$\ket{\Phi_+} = \frac{\ket{00} + \ket{11}}{\sqrt{2}}$$

est un état de Bell.

Exercice Montrez que

$$\mathsf{CNOT} = \frac{1_2 + Z}{2} \otimes 1_2 + \frac{1_2-Z}{2} \otimes X$$

Il existe une différence fondamentale entre les deux états \(\ket{++}\) et \(\ket{\Phi_+}\). L’état de bell ne peut pas se factoriser en un produit d’un vecteur de l’espace du premier qubit par un vecteur du second qubit EX. On dit que l’état est intriqué (“entangled” en anglais). Les implications physiques de l’intrication quantique sont fondamentales. L’intrication implique notamment qu’une description complète d’un système quantique, ici celui formé par deux spins, n’implique pas la connaissance de chacune de ses parties, ici ceci signifie que même si on connaît l’état de deux spins \(\ket{\Phi_+}\), on ne peut rien dire sur l’état, par exemple, du premier spin. Par contre, dans un état produit comme \(\ket{++}\), on peut dire (avec certitude) que le premier spin est dans l’état \(\ket{+}\). Comment donc décrire l’état du premier spin dans l’état de Bell? Il nous faut généraliser la notion d’état quantique. C’est le rôle de la matrice densité.

La matrice densité

Il nous faut d’abord maîtriser deux opérations sur les matrices : la trace et la trace partielle. Nous savons que la trace d’une matrice \(A\) est la somme de ses éléments diagonaux :

$$\Tr A = \sum_n A_{nn} = \sum_n a_n$$

où dans la première égalité \(A_{nn}\) sont les éléments de la diagonale de \(A\), et dans la deuxième égalité \(a_n\) sont les valeurs propres de \(A\): la trace ne dépend pas de la base :

$$\Tr A = \Tr (U A U^\dagger)$$

avec \(U\) la matrice (unitaire) de changement de base. Ceci est une conséquence de la propriété cyclique de la trace :

$$\Tr(ABC) = \Tr(CAB) = \Tr(BCA).$$

En particulier le produit scalaire peut donc s’exprimer par une trace :

$$\braket{\phi|\psi} = \Tr \ket{\psi} \bra{\phi}$$

ou

$$\braket{O} = \braket{\psi|O|\psi} = \Tr(\ket{\psi} \bra{\psi} O) = \Tr(\rho O)$$

avec \(\rho = \ket{\psi} \bra{\psi}\), comme on va le voir, la matrice densité.

Dans le cas où l’espace vectoriel peut s’écrire comme le produit de kronecker de deux espaces vectoriels on peut faire la trace sur l’un de sous-espaces, c’est la trace partielle. Soient \(A \in \mathcal{H}_A\) est \(B \in \mathcal{H}_B\) deux matrices des espaces \(A\) et \(B\), respectivement, on a

$$\Tr_B A \otimes B = A \Tr(B), \quad \Tr_A A \otimes B = B \Tr(A)$$

les traces partielles par rapport à \(B\) et \(A\). Par exemple EX,

$$\Tr_B (\ket{\Phi_+} \bra{\Phi_+}) = \frac{1}{2} 1_2.$$

two levels atom

Niveaux d’énergie d’un système de deux spins : l’état fondamental \(-3\) est non-dégénéré, tandis que l’état excité est dégénéré trois fois, et d’énergie \(1\). On considère une transition de l’état excité vers l’état fondamental due aux interaction du système avec, par exemple un laser.

En 1927, Landau publia un papier dans lequel il montra qu’à la suite des interactions un système composite, initialement dans un état produit, c’est-à-dire un état dans lequel chaque composant se trouve dans un état quantique bien défini, évolue vers un état intriqué: les interactions créent des corrélations quantiques qui interdissent toute spécification de l’état des sous-systèmes. Alors même que le système total reste dans un état pur (vecteur de l’espace de hilbert, de norme 1), l’état des sous-systèmes suit une distribution de probabilité. Pour décrire cette état statistique (et non plus “déterministe”) des sous-systèmes Landau introduisit la matrice densité. Voyons avec un exemple de quoi il s’agit.

Nous allons étudier deux spins \(1/2\) dont l’interaction est décrite par le hamiltonien EX:

$$H = X \otimes X + Y \otimes Y + Z \otimes Z = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 2 & 0 \\ 0 & 2 & -1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}.$$

Nous avons représenté dans la figure ci-dessus, les niveaux d’énergie (eigenvalues) ainsi que deux vecteurs propres (eigenvectors) correspondants EX (notez que la matrice est constituée de trois blocs). Supposons que l’état initial de deux spins est \(\ket{00}\), et qu’on applique un pic laser tel que le système transite vers l’état de basse énergie

$$\ket{s} = (\ket{01} - \ket{10})/\sqrt{2},$$

qu’on va appeler état singulet. Notre objectif est de caractériser l’état final de chaque spin, en particulier de mesurer leur intrication.

Voyons comment le laser transforme l’état initial avec les deux spins “up” dans l’état final “singulet”. On peut décrire l’action du laser par un circuit quantique (bien évidemment il s’agit d’un modèle ad hoc) EX

two level system

Système de deux spins ayant deux niveaux d’énergie : l’état excité (ici \(\ket{00}\)) triplement dégénéré, et l’état fondamental, le singulet \(\ket{s}\). Celui-ci est un état intriqué qui peut être obtenu à partir de l’état produit par application d’un pulse laser bien choisi.

Nous remarquons que \(\ket{s}\) c’est un état de bell, qu’on ne peu pas factoriser dans un produit de l’état du premier spin par le deuxième. Cependant, chacun des deux spins doit avoir une valeur (espérée) de \(\bm \sigma\) (l’observable spin est \(\bm \sigma/2\), en unités de \(\hbar\)); le problème est donc de calculer \(\braket{\bm \sigma}\), or pour cela il nous faut l’état du premier spin ! Il se trouve que la seule façon de calculer la valeur espérée du premier spin est d’introduire la trace partielle de l’état pur (celui du système total):

$$\braket{\bm \sigma} = \Tr(\rho_1 \bm \sigma), \quad \rho_1 = \Tr_2 \ket{s} \bra{s}$$

où on a \(\rho = \ket{s} \bra{s}\) la matrice densité du système total, et \(\rho_1 = \Tr_2 \rho\) la trace partielle, sur le spin 2 (sur son espace de hilbert), de l’état \(\rho\). Avec cette définition on généralise la notion de valeur observée d’une observable dans un état pur, au cas d’un état mixte, celui d’un sous-système d’un système dans un état pur. Le calcul de la trace partielle donne (voir l’exemple de l’état de bell plus haut)

$$\rho_1 = \frac{1}{2} 1_2 = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{pmatrix}.$$

Par conséquent, le spin de 1 est \(\braket{\bm \sigma} = 0\): la superposition de deux spins nous donne un spin nul dans l’état \(\ket{s}\). Vous pouvez vérifier que le spin de l’état initial est bien \(1/2 = (1/2) \braket{0|\bm \sigma|0}\).

Nous avons donc maintenant l’état de chaque spin (\(\rho_1 = \rho_2\)) sous la forme d’un état mixte :

$$\rho_1 = \frac{1}{2} \ket{0} \bra{0} + \frac{1}{2} \ket{1} \bra{1};$$

tout état mixte \(\rho\) peut s’écrire sous la forme

$$\rho = \sum_n p_n \ket{\psi_n} \bra{\psi_n}, \quad \sum_n p_n = 1$$

avec \(\ket{\psi_n}\) les états (pas forcément orthogonaux) des composantes et \(p_n\) la probabilité de cette état : l’état mixte est donc une distribution probabiliste d’états quantiques (comme par exemple l’ensemble de photons issues d’une source).

Notez que \(\rho_1\) n’est pas une superposition quantique, mais un “ensemble” dont les fréquences de spin up ou down sont juste \(1/2\). La conséquence de cet état statistique c’est qu’une succession de mesures du premier spin va nous donner une séquence aléatoire de 0 et 1 (up et down), comme si on jouait à jeter une pièce à pile ou face. Cependant, si corrélativement on obtient aussi une séquence de la mesure du second spin, elle sera le complément de la première séquence : si le premier spin est up, le second sera forcément down. Cette corrélation parfaite de deux séquences aléatoires est la manifestation de l’intrication du singulet, dont les deux spins sont “issus”.

Récapitulant, nous sommes partis d’un état produit de deux spins “up” \(\ket{00}\), et après l’application d’une transformation unitaire nous avons obtenu l’état de bell \(\ket{\Phi_+}\). Le fait que cet état ne puisse pas être factorisé, nous empêche de répondre simplement à la question “quel est l’état du, par exemple, le premier spin?”. Pour y répondre, nous avons introduit la trace partielle de l’état du système total (les deux spins), ce qui nous permet de établir l’identité

$$\braket{\bm \sigma} = \Tr \big( \bm \sigma \otimes 1_2 \ket{\Phi_+}\bra{\Phi_+}) = \Tr \bm \sigma \rho_1.$$

La matrice densité \(\rho\) généralise la notion d’état quantique aux systèmes mixtes. Ses propriétés principales sont

  • \(\rho = \rho^\dagger\) (hermitienne)
  • \(\Tr \rho = 1\) (normalisée)
  • \(\braket{\psi | \rho | \psi} \ge 0\) pour tout état \(\ket{\psi}\) (positive)
  • La valeur espérée de l’observable \(O\) est \(\braket{O} = \Tr (O \rho)\); pour un état pur \(\rho= \ket{\psi} \bra{\psi}\) on a \(\braket{O} = \Tr(O \ket{\psi} \bra{\psi}) = \braket{\psi|O|\psi}\).

Comment caractériser l’intrication d’un état quantique, comme celui dont les composantes ne peuvent pas être associées à un état pur (même si l’état du système est pur)? Une découverte essentielle de la mécanique quantique, due à von Neumann autour de 1930, est qu’on peut associer une entropie à un état quantique \(\rho\):

$$S = - \Tr\big( \rho \log \rho \big).$$

En diagonalisant la matrice densité

$$\rho = \sum_n p_n \ket{n} \bra{n}$$

où \(\{\ket{n}\}\) est une base complète et \(\{p_n\}\) l’ensemble de valeurs propres, on peut réécrire la formule de von Neumann sous la forme de l’entropie de Shannon :

$$S = -\sum_n p_n \log p_n.$$

L’entropie \(S\) est une mesure de l’intrication entre deux parties \(A\) et \(B\) d’un état pur \(\ket{\psi}\) de \(AB\). En effet, en prenant la trace partielle sur \(B\) de \(\rho_{AB} = \ket{\psi} \bra{\psi}\), le système total, nous avons l’état de \(A\), ce qui nous permet de calculer l’entropie de \(A\)

$$S_A = -\Tr \rho_A \log \rho_A, \quad \rho_A = \Tr_B \rho_A.$$

Le calcul de \(\rho_1\) dans l’état \(\ket{s}\bra{s}\) nous donne EX

$$S_1 = 1$$

le maximum de l’entropie d’un qubit ; on en conclue que le singulet est un état d’intrication maximale.

L’intrication est quantique

Prenons un état de trois qubits \(ABC\)

$$\ket{Q} = \frac{\ket{000} + \ket{111}}{\sqrt{2}}$$

où “Q” c’est pour quantique intriqué. Et considérons les observables \(O\) de l’espace \(\mathcal{H}_A \mathcal{H}_B \mathcal{H}_C\) définis par

$$O \in \{X \otimes Y \otimes Y, Y \otimes X \otimes Y, Y \otimes Y \otimes X\};$$

il est facile de vérifier que \(\ket{Q}\) est un vecteur propre de \(O\) avec valeur propre \(-1\)

$$O\ket{Q} = - \ket{Q};$$

ceci implique qu’une mesure \(m(O)\) de l’observable doit résulter en la valeur observée de \(-1\):

$$m_A(X) m_B(Y) m_C(Y) = -1$$

ce qui signifie que classiquement il existe une corrélation entre les mesures telle que quand on mesure deux \(Y\) et un \(X\) sur les trois appareils, le résultat est systématiquement \(-1\), même si les mesures de \(X\) ou de \(Y\), par exemple, peuvent résulter individuellement en \(1\) ou \(-1\). On en déduit la relation classique :

$$\big(m_A(X) m_B(Y) m_C(Y)\big) \big(m_A(Y) m_B(X) m_C(Y)\big) \big(m_A(Y) m_B(Y) m_C(X)\big) = m_A(X) m_B(X) m_C(X) = -1,$$

où on a utilisé le fait que \(m_A(Y)^2 = 1\), etc. En outre, l’opérateur quantique satisfait

$$\big(XYY\big) \big(YXY\big) \big(YYX) = -XXX$$

avec

$$XXX\ket{Q} = \ket{Q}$$

vecteur propre de \(\ket{Q}\) avec valeur propre \(1\) (on a omis les \(\otimes\) pour plus de clarté). Nous arrivons à une contradiction :

$$-1 = m_A(X) m_B(X) m_C(X) = 1.$$

Classiquement cette observable est \(1\) est \(-1\). L’hypothèse des corrélations entre les mesures ne peut donc pas expliquer les résultats de la mesure de l’ensemble d’observables \(O\) et \(XXX\). En résumé le raisonnement “classique”

$$\text{corrélations } + \text{condition } \big( XYY \rightarrow -1 \big) \Rightarrow \big( XXX \rightarrow -1 \big)$$

est en contradiction avec le fait que \(XXX \rightarrow 1\). Il faut insister sur le fait que le résultat obtenu est une propriété de l’ëtat \(\ket{Q}\), et non pas des observables qu’on a choisi pour révéler sa structure.

Cet exemple illustre le fait que la propriété intrinsèque des états quantiques qu’est l’intrication ne peut pas se ramener à une quelconque corrélation classique. En fait, si on utilise la mesure d’intrication de von Neumann, l’entropie de chaque spin, on trouve que l’intrication de chaque spin est maximale.

Mini-projet

États intriqués sur graphe

Dans ce mini-projet de recherche, nous allons étudier les états “cluster”, des états quantiques définis sur un graphe. Ceux-ci possèdent les propriétés physiques nécessaires pour pouvoir être utilisés comme ressource d’information dans le calcul quantique.

Effectivement, en plus de son intérêt fondamental l’information quantique s’applique au calcul quantique (quantum computation). En pratique le circuit quantique que transforme un état produit initial en état intriqué, lequel sert de ressource algorithmique, est un modèle de calcul quantique. Un exemple paradigmatique est l’algorithme de Shor (1994) de factorisation d’un entier ; cet algorithme démontra les possibilités d’un éventuel ordinateur quantique. L’élément essentiel de tout algorithme quantique est un état intriqué. Un exemple représentatif est celui de la téléportation. Notre tâche sera maintenant de créer des états intriqués définis sur un graphe. Ces états sont, pour un graphe suffisamment complexe, une ressource universelle du calcul quantique ; grosso modo ceci signifie qu’on peut implémenter n’importe quel unitaire sur \(N\) qubits, par une séquence de mesures et de transformations à un qubit, de cet état.

Commençons par définir un graphe : c’est un ensemble de points, les nœuds, qu’on relie par de segments, les liens. L’ensemble de nœuds est \(V\), et celui de liens \(E\); on note \(x\in V\) un élément de \(V\) et la paire \((x,y)\in E\), un élément de \(E\). Par exemple le graphe

graph diagonale

est défini par le couple \((V,E)\):

$$V = \{0, 1, 2, 3\}, \quad E = \{(0,1), (0,2), (0,3), (1,2), (2,3)\},$$

le nombre de nœuds est \(|V| = N = 4\) et celui de liens \(|E| = 5\). Nous allons associer un qubit à chaque nœud, ce qui nous permet d’associer l’état de ces \(N\) qubits à un état du graphe. Initialement, cet état est un produit des états propres de \(X\), \(\ket{+}\):

$$\ket{++\ldots} = \ket{+} \otimes \ket{+} \otimes \ldots = \ket{+}^{\otimes N}.$$

L’état cluster \(\ket{C}\), résulte de “l’interaction” des qubits voisins (reliés par un lien); on choisit pour cette interaction la porte phase-contrôlée :

$$\mathsf{CZ} = \mathrm{diag}(1,1,1,-1),$$

c’est-à-dire

$$\ket{C} = \prod_{(x,y) \in E} \mathsf{CZ}(x,y) \ket{+}^{N}$$

(comprenez le produit comme produit tensoriel). Cette “gate”, apparenté à l’interaction \(ZZ\) (d’Ising), produit de l’intrication. L’exemple le plus simple est celui de deux qubits \(\ket{++}\):

cphase ++

$$\mathsf{CZ}\ket{++} = \frac{1}{2}\big( \ket{00} + \ket{01} + \ket{10} - \ket{11} \big) = \frac{\ket{0+} + \ket{0-}}{\sqrt{2}} = \ket{C_2}$$

donc, après l’application de \(\mathsf{CZ}\) on obtient le cluster \(\ket{C_2}\) de deux qubits (remarquez la similitude de l’action de la phase contrôlée sur la base \(\ket{\pm}\) avec celle du non contrôlé sur la base \(\ket{0}\), \(\ket{1}\)).

Sujet

Nous allons explorer les propriétés d’intrication des états cluster sur différents graphes, avec un premier objectif de caractériser leur intrication en fonction de la géométrie du graphe : est-ce l’entropie d’intrication une grandeur extensive, comme en thermodynamique?

Codes

Voici quelques exemples python qui pourront vous être utiles dans la résolution des exercices.

import sympy as sy 
#
theta, phi = sy.symbols("theta, varphi", real = True)

# Base de l'espace de hilbert fe
ket_0 = sy.Matrix( [1,0] )
ket_1 = sy.Matrix( [0,1] )
# Definition des matrices

# un
i = sy.I
I = sy.Matrix( [[1,0],[0,1]] )

# pauli
X = sy.Matrix( [[0,1], [1,0]] )
Y = sy.Matrix( [[0,-i], [i,0]] )
Z = sy.Matrix( [[1,0],[0,-1]] )

# phase
def S(phi):
    return sy.Matrix( [[1,0],[0, sy.exp(i*phi)]] )

# qubit
ket_psi = sy.cos(theta/2) * ket_0 + sy.sin(theta/2)*sy.exp(i*phi) * ket_1
# bloch shpère
nx = sy.simplify( ket_psi.H * X * ket_psi )
ny = sy.simplify( ket_psi.H * Y * ket_psi )
nz = sy.simplify( ket_psi.H * Z * ket_psi )
n = sy.Matrix( [nx, ny, nz] )

# interféroèmtre
B = (I + i*X)/sy.sqrt(2)
out = B*S(phi)*B * ket_0
amplitude = ket_1.H * out
# probabilité en D = 1
p_1 = sy.simplify(sy.expand(sy.conjugate(amplitude)*amplitude))

### DEUX SPINS
from sympy.physics.quantum import TensorProduct as TP
# TP est le produit de kronecker
# base de hilbert dim = 4
base = sy.Matrix([TP(ket_0,ket_0).T, TP(ket_0,ket_1).T,
                 TP(ket_1,ket_0).T, TP(ket_1,ket_1).T])
# interaction sigma.sigma
ising = TP(X,X) + TP(Y,Y) + TP(Z,Z)
# calcul du "spectre"
spectre = ising.eigenvects()

Intrication

# numpy
import numpy as np
# scipy
from scipy.linalg import eigvals, svdvals

def np_a(M):
    # conversion d'une matrice sympy en un tableau numpy
    return np.array(M).astype(np.complex128)

def partial_tr(A):
    # dim a = N = 2^L, pour L qubits
    N = len(A)
    n = 2**(int(np.log2(N))//2)
    aa = A.reshape((n,n,n,n)) # partition en deux parties égales    
    return np.einsum('ijkj->ik', aa)

def entropy_vn(rho):
    # entropy de von Neumann (non optimisée)
    rho_1 = partial_tr(rho)
    pn = np.real(eigvals(rho_1)) # valeurs propres
    n = pn > 0 # test si valeurs propres 0
    if len(n) > 0:
        S = -np.sum( pn[n] * np.log2(pn[n]) )
    else:
        S = 0.0 # p log p = 0 if p = 0
    return S

# singulet
s = (base[:,1] - base[:,2])/sy.sqrt(2)
rho = np_a(s*s.T) 
rho_1 = partial_tr(rho) # -> 0.5 Id
entropy_vn(rho) # -> 1 intrication maximale!

État graphe (cluster)

# numpy
import numpy as np
# scipy
from scipy.linalg import eigvals, svdvals

#
# ETAT CLUSTER
# spin indices
def s_dd(x, y, N):
    """liste de configurations (s_0...s_{2^N-1}) de N qubits 
    avec s_x = 1 et s_y = 1
    """
    s = np.arange(2**N) # set of spin configurations
    sx = np.mod( s//2**(N-1-x), 2 ) # adresse du spin x (s_x = 0,1)
    sy = np.mod( s//2**(N-1-y), 2 ) # adresse du spin y (s_y = 0,1)
    return np.intersect1d(np.flatnonzero(sx == 1) , np.flatnonzero(sy == 1))
# état C = Prod CPHASE(edges) |+++...>
def cluster_C(E, N):
    """état cluster d'un graphe E (liens)
    """
    C = np.ones((2**N))/np.sqrt(2**N) # produit tensoriel |++++...>
    for x, y in E:
        l = s_dd(x, y, N)
        C[l] = -C[l]
    return C
# entropie
def entropy(C, N):
    """on utilise la décomposition en valeurs singulières
       de l'état pur; entropie de N//2 qubits
    """
    r = C.reshape((2**(N//2), 2**(N - N//2)))
    ev = svdvals(r)
    pn = np.real(ev**2)
    pn = pn[pn > 0]
    return -sum(pn*np.log2(pn))
#
# application: triangle
N = 3
E = [(0,1), (1,2), (2,0)] # liens
entropy(cluster_C(E, N), N)

Bibliographie

Index