Leçon de physique théorique: Quantum state teleportation

mar. 07 mars 2017
Blog
#teaching

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\K}[1]{\left|#1\right\rangle}$

This lecture is intended for students of the “Licence de physique”, and in particular to those interested in theoretical physics.

In classical physics the unit of information is the bit. The number $M$ of different messages with $n$ letters $x$, taken on an alphabet of two letters $x=0,1$ (bit), distributed according to the probability $p(x)$ is

$$M = 2^{nS(p)}, \quad S(p) = -\sum_x p(x)\log_2 p(x)$$

where $S$ is the Shannon entropy. Hence, $S$ is the averaged content of information, measured in bits, of a single letter $x$.

In quantum physics the unit of information is the qubit. Physically a qubit can be carried by a spin $1/2$ particle. The quantum state $|\psi\rangle$ of this particle is in general a superposition of spin up $\K{0}$ and spin down $\K{1}$ states:

$$\K{\psi} = a\K{0} + b\K{1}$$

with the complex amplitudes satisfying the normalization $|a|^2 + |b|^2 = 1$. A mixture of such states $|\psi_n\rangle$, can be described by the density matrix,

$$\rho = \sum_n p_n |\psi_n\rangle \langle \psi_n|\,.$$

Von Neumann associated an entropy to a mixed quantum state,

$$S(\rho) = - \mathrm{Tr}\, \rho \ln \rho,$$

which, by analogy with the Shannon entropy, is a measure of the information contained in the state $\rho$ (in quantum information one replaces the natural logarithm by the base 2 one). In particular, for a mixed system of spins up and down, the density matrix is given by

$$\rho = p |0\rangle \langle 0| + (1-p) |1\rangle \langle 1|,$$

from which we obtain for the entropy, the same result as in the classical state: one qubit contains one bit of information. However, two qubits can contain more information than two bits, the difference comes from a quantum effect that do not have a classical counterpart: entanglement. Entangled states are states of a composite system that cannot be splitted into a tensor product of the component states. For instance there are two qubit states $|\psi\rangle$ that cannot be written as a product $|\psi\rangle = |x\rangle \otimes |y\rangle$, where $|x\rangle$ and $|y\rangle$ are qubits.

In the following we will use the entanglement as a resource to transfer a quantum state form one position to another one, this process is called teleportation. Why do we need entanglement? Because it is impossible, in general, to copy a quantum state. Indeed, we can demonstrate the non-cloning theorem:

Non-cloning theorem Cloning a state suppose the existence of an unitary $U$ such that, when applied to a state $\K{\psi}$ it gives
$$U \K{\psi} \otimes \K{0} = \K{\psi} \otimes \K{\psi} = \K{\psi \psi}$$
Applying it to another state,
$$U \K{\phi} \otimes \K{0} = \K{\phi \phi},$$
and computing the scalar product of these two states, one gets:
$$\langle \psi | \phi\rangle =\left(\langle \psi | \phi \rangle\right)^2$$
which cannot be satisfied by arbitrary states.

Therefore, in order to transfer a quantum state we need a smarter recipe.

The idea is to use the quantum correlation characteristic of an entangled state, which persists even if the corresponding qubits are spatially separated (nonlocality of the quantum state). Making at some place a measure on one of the entangled qubits, allows to predict the result on the measure of the pairing qubit, located at another place.

A quantum state can be manipulated using unitary operators. A sequence of such operations (gates) form a quantum circuit. Some elementary one qubit gates are the Pauli matrices $X,Y,Z$

$$X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\,,\quad Y = \begin{pmatrix} 0 & -\I \\ \I & 0 \end{pmatrix}\,,\quad Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\,,$$

and the Hadamard matrix $H$

$$ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}$$

For example, the Hadamard gate acts as:

$$H:\;\K{0}\rightarrow \frac{\K{0} + \K{1}}{\sqrt{2}} = \K{+},\quad \K{1}\rightarrow \frac{\K{0} - \K{1}}{\sqrt{2}} = \K{-}.$$

The controlled not $\mathrm{CNOT}$ is a gate acting on two qubits:

$$\mathrm{CNOT}:\; \K{x,y} \rightarrow \K{x, x\oplus y}$$

where $\oplus$ is the addition modulo 2,

$$\mathrm{CNOT} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}\,.$$

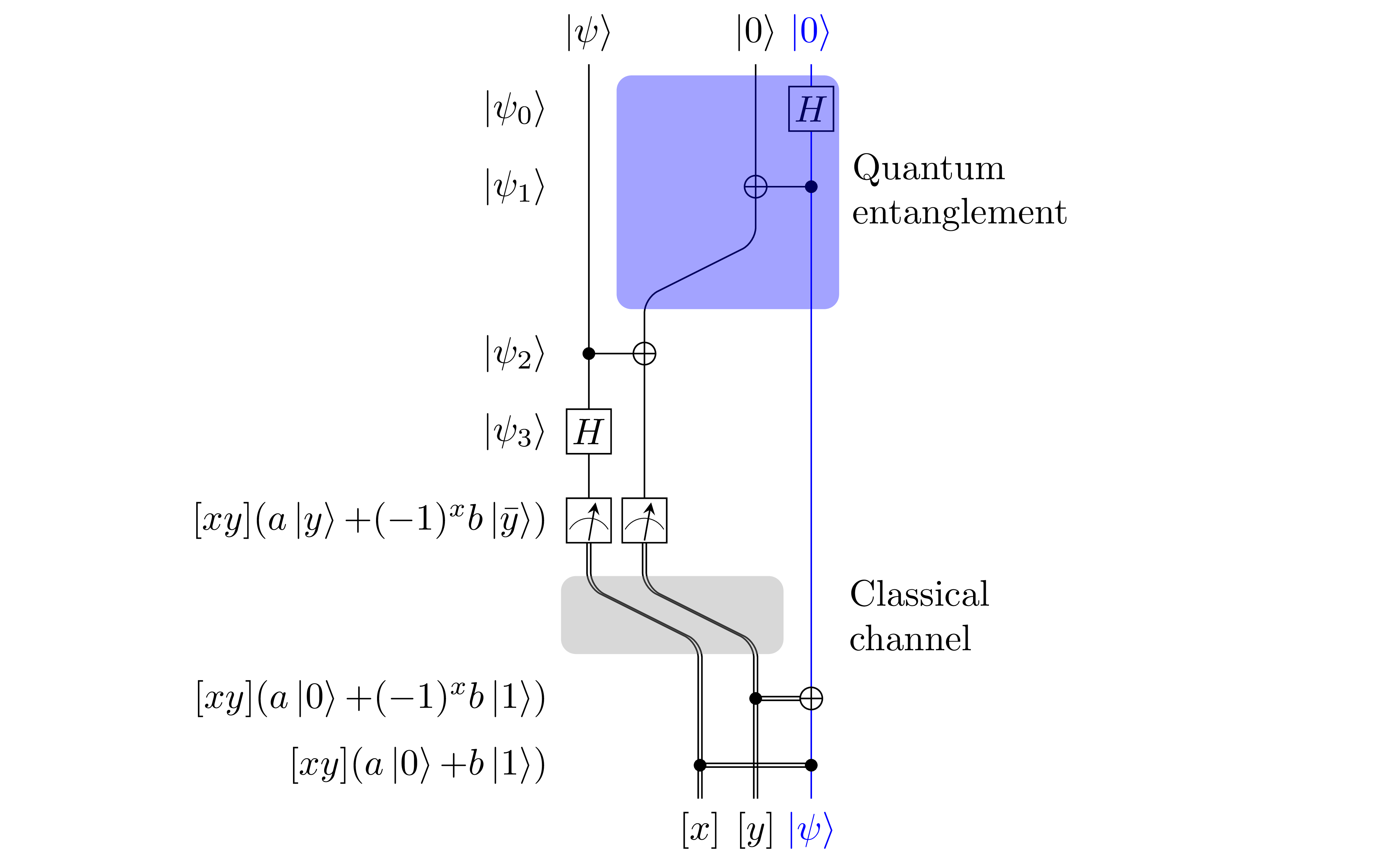
The teleportation algorithm can be implemented as a quantum circuit (see the figure above), consisting in the following steps:

Initial state, the quantum state we want to teleportate is qubit 1 (channel 1), the other two qubits are spins up (at channels 2 and 3):

$$\K{\psi_0} = \K{\psi}\K{00}=a\K{000}+b \K{100}$$
First, entangle qubits 2 and 3, initially $|00\rangle$, using the Hadamard gate on channel 3 and a $\mathrm{CNOT}$ (controlled by the qubit in channel 3):

$$\K{00} \rightarrow H \rightarrow \frac{1}{\sqrt{2}}(\K{00} + \K{01}) \rightarrow \mathrm{CNOT} \rightarrow \frac{1}{\sqrt{2}}(\K{00} + \K{11}) = \K{B_{00}}$$
Now we have the unknown state $|\psi\rangle$ coupled with an entangled state (Bell state $|B_{00}\rangle$):

$$\K{\psi_1} = \frac{a}{\sqrt{2}} \left(\K{000} + \K{011}\right) + \frac{b}{\sqrt{2}} \left(\K{100} + \K{111}\right)$$
Apply the $\mathrm{CNOT}$ gate (control qubit 1):

$$\K{\psi_2} = \frac{a}{\sqrt{2}} \left(\K{000} + \K{011}\right) + \frac{b}{\sqrt{2}} \left(\K{110} + \K{101}\right)$$

this operation entangles the unknown state with the bell state.
Apply the Hadamard gate (superposition of qubit 1):

$$\K{\psi_3} = \frac{a}{2}\left( \K{000} + \K{100} + \K{011} + \K{111}\right) + \frac{b}{2}\left( \K{010} - \K{110} + \K{001} - \K{101}\right)$$

The obtained state can be rewritten to factor out the $a$ and $b$ terms, and grouping terms in the two bit base $|\cdot \cdot\rangle$:
\begin{align*} \K{\psi_3} & = \frac{\K{00}}{2}\left( a\K{0} + b \K{1} \right) \\ & + \frac{\K{10}}{2}\left( a\K{0} - b \K{1} \right) \\ & + \frac{\K{01}}{2}\left( a\K{1} + b \K{0} \right) \\ & + \frac{\K{11}}{2}\left( a\K{1} - b \K{0} \right) \end{align*}
Now, measuring the first two qubits and transmitting this classical information to channel 3 (perhaps located far away channels 1 and 2), it is possible to obtain the state initially in channel 1. Depending on the measure results, say the pair of bits $[x]$ and $[y]$, the channel 3 contains the vector

$$\K{\psi_{33}} = a \K{y} + b (-1)^x \K{\bar{y}}$$

with $\bar{y}=-y$ (the 3th channel part of the qubit $|\psi_3$). Therefore, the transformation

$$Z^y X^x \K{\psi_{33}} = \K{\psi}$$

finally gives the original state, now at channel 3.

Bibliography and tools

Information theory and quantum computation

Nielsen, M. and Chuang, I. “Quantum computation and quantum information”, Cambridge University Press (2010)
Shannon, C. “A mathematical theory of communication”, The Bell System Technical Journal 27, 379 (1948) .pdf

Quantum circuit drawing

Draper, T and Kutin, S. “$\langle q|pic\rangle$: Quantum circuit diagrams in LaTeX” (2016)

Symbolic calculus, including quantum mechanics

SymPy: symbolic computing in Python PeerJ Computer Science 3:e103 (2017)