$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bm}[1]{\boldsymbol{#1}}$

Topological and random phases in a spin ladder¹

Introduction

I therefore believe it’s true that with a suitable class of quantum machines you could imitate any quantum system, including the physical world (Feynman, 1982).²

Indeed, present “noisy intermediate scale quantum computers” are already suitable to simulate (imitate) nonequilibrium many-body systems,³ and explore exotic phases of matter⁴ (like the Kosterlitz-Thouless phase of superfluid films, the fractional quantum Hall effect, or the topological phases in spin liquids with non-abelian excitations.⁵) It is therefore desirable to find simple, rich models with nontrivial entanglement patterns, thus beyond the reach of a classical computer but amenable to be implemented in a quantum simulator.

Entanglement is a resource of quantum information, as can be measured by the von Neumann entropy. However, not all forms of entanglement are useful for quantum computing. It is well know that maximally entangled random states are algorithmically equivalent to classical (thermal) states. This observation extends to small subsystems of thermal states, which are essentially unentangled. Symmetry protected topological states are, at variance, suitable resources; for instance their excitations can be used to build fault tolerant gates.⁶

Symmetry protected topological states can be constructed from a set of stabilizers, as the ground state of a Hamiltonian. An important example is the so called cluster state, which is a universal resource for measurement-based quantum computation.⁷ In the one-dimensional case the cluster state $\ket{C}$ is the ground state of the Hamiltonian

$$ \begin{equation} \label{e:HC} H_C = -J\sum_{x=1}^L Z_{x-1} X_x Z_{x+1} \end{equation} $$

where at each site $x$ of a lattice (of step $\Delta x=1$) is located a qubit ($1/2$-spin), and $(X,Y,Z)$ are the Pauli matrices; the exchange energy $J$ is positive ($\hbar=1$). The cluster state is then,

$$ \begin{equation} \label{e:C} \ket{C} = \prod_{x=1}^{L} \mathsf{CZ}(x,x+1) \ket{+}^L \end{equation} $$

where $\ket{+}$ is the eigenvector of $X$ with eigenvalue 1, and $\mathsf{CZ}= \mathrm{diag}(1,1,1,-1)$ is the control-phase gate (the exponent refers to the dimension $2^L$ of the Hilbert space of $L$ qubits). Note that the construction of the cluster state can be easily generalized to an arbitrary graph $G(V,E)$, applying $\mathsf{CZ}$ to its edges $E$ (the order can be arbitrary, since the gates on different edges commute); in this case the stabilizers are of the form

$$ K_x = X_x \prod_y Z_y, \quad x\in V, \; (x,y) \in E $$

where $x$ is a vertex and $(x,y)$ are its incoming edges. In ($\ref{e:C}$) the three-body interaction $K = ZXZ$ are the stabilizers of $\ket{C}$.

The cluster state is the unique ground state of ($\ref{e:HC}$) in the case of periodic boundary conditions; for open boundary conditions, it becomes four-fold degenerated: This is a manifestation of the the $\mathbb{Z}_2 \times \mathbb{Z}_2$ symmetry generated by the parity operators

$$ \begin{equation} P_e = \prod_{x \in e} X_x, \; P_o = \prod_{x \in o} X_x, \quad [P_{e,o}, H_C] = 0 \end{equation} $$

where $x$ runs over the set $e$ of even sites, and $o$ of odd sites, respectively. The entanglement entropy associated to a bipartition $\mathrm{A} = \mathrm{A}_1 \cup \mathrm{A}_2$ (with $|\mathrm{A}_1| = |\mathrm{A}_2| = |\mathrm{A}|/2$) is $\mathcal{S}_{A_1} = 4$, independent on the length $L$ of the spin chain (we have two cuts with periodic boundary conditions, and $2$ bits of entropy per cut). Excitations above the ground state can be generated by the raising operator $Z + \I ZYZ$, and are separated to the cluster state by a gap of $2J$.

The cluster Hamiltonian is one of the simplest models, like the polyacetylene or the valence-bond models, exhibiting a topological phase (at zero temperature) and protected by symmetry. However, its entanglement is short range: Using local unitaries one may transform it in a product state, as is evident from the algorithm ($\ref{e:C}$) to build it, which involves only Clifford group gates; moreover, universality is obtained by measurement, an irreversible transformation of the state. Therefore, one may naturally ask whether some unitary generalization of the model would lead to high-energy topological states.

In this work we address the problem of the persistence of a topological phase under nonequilibrium conditions, and of the correlative entanglement transitions. In addition to its interest as a simple model allowing to test the capabilities of noisy quantum computers and to provide a recipe to build a useful highly entangled state to quantum information processing, it also let us investigate the rich phenomenology of excited states in many-body systems created by a discrete time dynamics.

To reach this goal we must generalize the cluster model, in particular by introducing a dynamics involving non Clifford gates, which is a necessary condition to evolve towards states with a robust entanglement structure, beyond ground states of simple Hamiltonians. For example, Floquet engineering is a standard technique to create gates from simple Hamiltonians, based on the fact the the composition of two unitaries leads to a nontrivial effective Hamiltonian. Another example is the “monitored” circuit of random unitaries, in which one introduces a probability that a qubit be measured in such a way that, when the measurement frequency increases, the system undergoes a transition from high to low entanglement.⁸

We adopt here the automaton model of quantum computing, which is equivalent to the universal circuit model, to define the dynamics of a combination of the “cluster” chain and a set of independent spins, which we call the “environment”, together with an exchange interaction between both subsystems. We investigate the entanglement properties of the cluster subsystem, in particular to probe the persistence of the topological phase and the eventual generation of a long-range entangled stationary state.

Model

The system consists in a ladder of qubits (one-half spins) in which A is the cluster subsystem and B is the environment subsystem, formed by free spins. The cluster spins interact via a three-body exchange interaction $J$; the two subsystems are coupled via a swap spins interaction of strength $g$.

Instead of the simple cluster chain, we consider a ladder of $L$ cells A and B; each cell $x=1,\ldots,L$ contains two qubits (figure above). The automaton dynamics is generated by the one-step unitary

$$ \begin{equation} \label{e:U} \mathsf{U}(J,g) = \prod_{x=1}^L \mathsf{C}_x(J) \prod_{x=1}^L \mathsf{SW}_x(g), \quad \mathsf{C}_x(J) = \E^{\I J Z^\mathrm{A}_{x-1} X^\mathrm{A}_x Z^\mathrm{A}_{x+1}}, \; \mathsf{SW}_x(g) = \E^{(\I g/2)(X^\mathrm{A}_x X^\mathrm{B}_x + Y^\mathrm{A}_x Y^\mathrm{B}_x)} \end{equation} $$

where the Pauli matrices act over the $x$ sites of sublattices A or B; we note that these two gates $\mathsf{C}$ and $\mathsf{SW}$ do not commute when applied to shared cells AB. For an initial state $\ket{\psi(0)}$, $t$ iterations of the automaton give the state

$$ \begin{equation} \label{e:psit} \ket{\psi(t)} = \mathsf{U}^t(J,g) \ket{\psi(0)}. \end{equation} $$

We take $\ket{\psi(0)} = \ket{C} \ket{+}^L$ as the initial state, the tensorial product of the cluster state ($\ref{e:C}$) for the cluster subsystem, and an unentangled environment state for the B sublattice. A sketch of the automation is represented in the figure below.

The dynamics of the lattice system, presented in the previous figure, is defined by a two layers automaton; the first unitary layer comprises a set of swap gates $\mathsf{SW}$ acting on A and B qubits; the second layer acts only on the A sublattice, by a set of commuting three-body gates $\mathsf{C}$ associated to the cluster Hamiltonian. The automaton is thus defined by the unitary $\mathsf{U}(J,g)$ of Eq. ($\ref{e:U}$).

In this simple nonequilibrium model the distinction between “system” (the cluster subsystem) and “environment” is allowed by the different interactions characterizing both sublattices: The cluster three-body interaction of strength $J$, and the independent spins of the environment sublattice. The evolution of the “environment” therefore only depends on its interaction with the “system”, whose strength is $g$. However, contrary to a standard environment, the number of free spins is here identical to the number of cluster spins. Another obvious difference with, for instance a thermal bath, is that the state of the free sublattice is not fixed, determined by a few constant macroscopic parameters like the temperature, but evolves jointly with the cluster subsystem towards an eventual statistically stationary nonequilibrium state (the discrete time breaks the energy conservation).

The role of the free spins is, in the present model, to irreversibly modify the initial cluster state through entanglement scrambling, in much the same way as can be done by projecting some qubits to their up state in monitored systems. The free spins can be thought as auxiliary qubits that, through the swap gate, introduce errors in the cluster code. This kind of setup was already used by the Google team (Mi et al. 2024)⁹ to mimic the monitored dynamics using an unitary circuit and deferred measurements.

The main question is whether the interaction with the free spins can lead the cluster subsystem towards a topological phase with long-range entanglement. It is well known that $X$ measurements of a subset of the spins in the cluster state results in a state unitary equivalent to the Greenberger-Horne-Zeilinger, which is an example of long-rang entangled state.

Quantum phase transition in the mean-field and Markov approximations

We shall study if the topological phase possibly persists under the dynamics ($\ref{e:psit}$) in two analytically tractable approximations: When $(J,g) \ll 1$ are small, allowing the definition of an effective local mean-field Hamiltonian; and when the system state is random enough to consider the dynamics to be Markovian, such that at each time step the state of the system can be separated between the two subsystems.

The mean-field Hamiltonian $\bar{H}$,

$$ \begin{equation} \bar{H}(k) = \begin{pmatrix} -2J s_B^2 \cos 2k + g s_B & -2J s_B^2 \sin 2k & -g & - \I g \\ -2Js_B^2 \sin 2k & 2Js_B^2 \cos 2k - g s_B & -\I g & g \\ -g & \I g & 0 & 0 \\ \I g & g & 0 & 0 \end{pmatrix}, \end{equation} $$

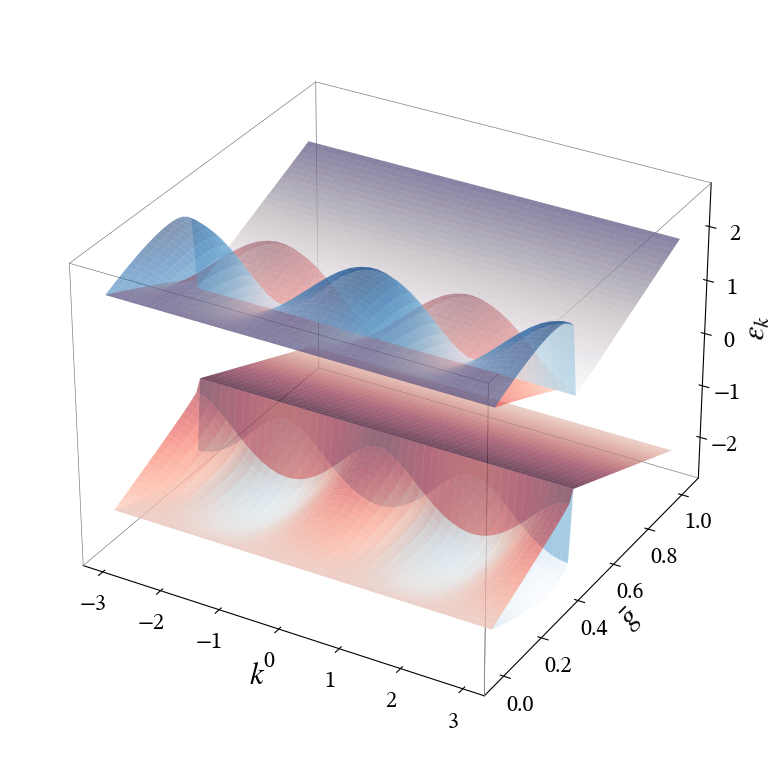
is obtained using the standard Wigner-Jordan mapping of the Pauli matrices into fermions, which leads to a local quartic expression. This expression can be simplified by the introduction of the environment average magnetization $s_B = \braket{X_x^\mathrm{B}}$, and by Fourier transformation into $k$-space to account for the translation invariance. The expected value $\braket{X_x^\mathrm{B}}$ must be computed self-consistently in the ground-state of the mean-field Hamiltonian. After a Bogoliubov transformation one obtains the dispersion relation (quasi-energies)

$$ \begin{equation} \varepsilon_k = 2 \sqrt{(J s_B - g)^2 s_B^2+ g^2 + 4J s_B^3 g \sin^2 k}, \end{equation} $$

and the selfconsistent equation for the mean-field

$$ \begin{equation} s_B = \int_{-\pi}^\pi \frac{\D k}{2\pi} \frac{2g^2}{\varepsilon_k^2 - 2g^2} - 1, \end{equation} $$

which leads to

$$ \begin{equation} \pm s_B = 1 - \frac{\bar{g}^2}{\sqrt{4 s_B^8 - 8 \bar{g}^2 s_B^6 + 4 \bar{g}^2 (1 + \bar{g}^2) s_B^4 + \bar{g}^4 (4 s_B^2 + 1)}}. \end{equation} $$

One observes that, in the mean-field approximation, the spectrum $\varepsilon_k = \varepsilon_k(\bar{g})$ and the magnetization $s_B = s_B(\bar{g})$ only depend on the reduced parameter $\bar{g} = g/J$; this is not the case of the automaton rule for which $J$ and $g$ are independent parameters.

Mean-field magnetization of the environement in the ground state of $\bar{H}$ and dispersion relation $\varepsilon_k$ as function of the cluster-free spins coupling $\bar{g}=g/J$.

We find a first order phase transition, as revealed by the discontinuity of the environment magnetization at $\bar{g} = 0.425 = \bar{g}_c$. This suggests that the cluster phase might persist below $\bar{g}_c$, since nowhere the gap in the quasi-energy $\varepsilon_k$ closes. Above $\bar{g}_c$ the magnetization vanishes, and a disordered phase might thus arise. The quasi-energy bands become flat above the critical coupling $\bar{g}_c$, and the gap grows linearly in $\bar{g}$.

These observations raise the question about the entanglement across the phase transition; in particular we may ask if there is a change in the topological properties of the stationary state reached by the automaton, and if this change eventually corresponds to an entanglement transition between a high and a low entanglement state of the cluster subsystem. To address this question we first investigate a Markovian approximation of the automaton.

The Markov dynamics is obtained from the partial trace over the free spins of the discrete time dynamics:

$$ \begin{equation} \label{e:markov} \rho(t + 1) = \Tr_B \big[ U\rho_{AB}(t) U^{\dagger}\big] = \sum_n M_n \rho(t) M_n^\dagger, \quad M_n = \braket{n_B|U|t_B}, \end{equation} $$

where $\rho_{AB}$ is the density matrix corresponding to the pure state of the cluster-environment global system and $\ket{n_B}$ is a basis of the environment Hilbert space and $\ket{t_B}$ its state at time step $t$; moreover, we denoted $\rho = \rho_A$ the cluster density matrix (in this context we do not need to specify the label A of the cluster subsystem), and defined $M_n$, the Kraus operators, by

$$ \begin{equation} \label{e:Mn} M_n = u_0 \cos^{L-|n_+|} \frac{g}{2} \sin^{|n_+|} \frac{g}{2} \Big(\prod_{x\in n_+} \E^{-\I gX_x} Y_x \Big) \end{equation} $$

where $u_0 = \exp{(-\I J H_{0})}$ is an evolution operator associated with the (non-equilibrium) Hamiltonian

$$ \begin{equation} H_0 = -\sum_{x=1}^L \Big( Z_{x-1} X_x Z_{x+1} + \frac{\bar{g}}{2} X_x \Big), \end{equation} $$

identical to a cluster Hamiltonian in a symmetry preserving field $\bar{g}/2$. The expression of $M_n$ contains the number $|n_+|$ of 1 in the binary expansion of the integer $n = 0,\ldots,2^L - 1$ ($n_+$ is the set of 1 positions in this expansion): This corresponds to the number of simultaneous “errors” $Y_x$. To obtain ($\ref{e:Mn}$) we assumed a limit of small $J$ ($\bar{g}$ can be of order one, and in our units $J=J\Delta t$), and, in this limit, we assumed that at each time step the density matrix separates between the two subsystems, leading to the usual Markov form in which the actual state of the system only depends on its preceding state.

Usually, in the Lindblad approximation, one consider stochastic processes in which the probability of simultaneous errors are negligible. In our model, at variance, the relevant term is the one in which we have $L$ simultaneous $Y$ flips of the environment spins: This ensures perfect synchronization of the homogeneous environment state. In this case the Markov equation simplifies to

$$ \begin{equation} \label{e:ML} \rho(t+1) = u_0 \sin^{2L}\frac{g}{2} \Big(\prod_x \E^{-\I g Y_x} Y_x \Big) \rho(t) \Big(\prod_x Y_x \E^{\I g Y_x} \Big) u_0^\dagger. \end{equation} $$

An important outcome of this equation is that the stochastic process preserves the parity symmetry of the original cluster system, a so called “strong” symmetry

$$ \begin{equation} [H_0,P] = 0, \; PM_LP = M_L, \quad P = \prod_x X_x, \end{equation} $$

where the product is over even or odd sites of sublattice A. As a consequence we find that the cluster topological phase can be protected by the parity symmetry $P$, at least in this approximation, for finite values of $\bar{g}$. Moreover, the form of the deterministic Hamiltonian $H_0$ suggests the existence of a critical value $\bar{g}_R = 2$, which separates a cluster dominated regime to a random one dominated by the free spin generated effective field.

Entanglement transition

To assess the entanglement properties of the cluster system we measure the negativity entanglement spectrum, using exact numerical computations of the whole quantum state. The negativity spectrum is obtained from the eigenvalues $\lambda_n$ of the reduced density matrix $\rho_A^{T_1}$, where $T_1$ is the partial transposition over a bipartition of A into parties 1 and 2 of equal size. The (logarithmic) negativity itself is given by

$$ \begin{equation} \label{e:N} \mathcal{N} = \log\Big(\sum_n |\lambda_n| \Big), \quad n=1, \ldots, \mathrm{dim}\rho_A \end{equation} $$

where $\mathrm{dim} \rho_A=L$ in our case, and $\log$ is for the base 2 logarithm. The minimum eigenvalue we denote $\lambda$ is an entanglement witness, it vanishes for unentangled states and is negative for entangled states. The automaton evolves from an initial (entangled) cluster state ($\ref{e:C}$) for the A sublattice and a product state for the B one,

$$ \begin{equation} \label{e:ini} \ket{\psi(0)} = \ket{C} \ket{+}^L, \quad X\ket{+} = \ket{+}, \end{equation} $$

in which the negativity is $\mathcal{N}=2$.

Entanglement transition. Minimal negativity eigenvalue $\lambda$ as a function of the environment strength coupling parameter $g$ for different values of the cluster exchange energy $J=0.2,0.3,0.4$; the inset shows the same data but as a function of the reduced parameter $\bar{g}=g/J$. The system size is $2L=20$. The value of the critical parameter $\bar{g}_c$ (mean-field) is shown by the dotted line.

The behavior of $\lambda$ as a function of $\bar{g}$ (the figure above demonstrate that it is the good parameter), shows an entanglement transition around the critical value predicted by the mean-field approximation: For small $\bar{g} \ll \bar{g}_c$, the minimum negativity eigenvalue remains near its cluster value ($\lambda = 0.25$), while for larger values it saturates to its maximum $\lambda = 0$ signaling an unentangled (random) state of the cluster subsystem. The low entanglement phase is a result of the entanglement scrambling, the spreading of quantum information over the whole Hilbert space, leading to a vanishing entanglement within subsystems. This entanglement transition, should reflect the persistence of the cluster topological phase when the influence of the environment is weak, and of a thermal phase in the opposite limit of strong environment influence. For large values of $J$ and $g$, as usually in Floquet quantum systems, one expects an evolution towards an infinite temperature thermal state.

Before analyzing the topology of the low $\bar{g}$ phase, we characterize the entanglement properties of the cluster and environment subsystems using the entanglement entropy.

Entanglement entropy for $\bar{g} = 0.2, 0.5, 2.0$ (from left to right), corresponding to states in the cluster phase, in the transition parameter region, and in the random (thermal) phase, respectively. Size $2L=16$.

In the above figure we illustrate the entanglement behavior of the system using the von Neumann entropy. The half system entropy, from a bipartition of the whole ladder comprising A and B spins, is denoted $\mathcal{S}$; the B chain of independent spins entropy is $\mathcal{S}_B$; and the logarithmic negativity, measuring the entanglement of the (open) cluster lattice A, is the $\mathcal{N}$ given in ($\ref{e:N}$).

The first panel shows the typical behavior of the system for small values of $J$ and $g$ with $\bar{g} < \bar{g}_c$, in the cluster phase region; the total entropy is dominated by the entanglement in the cluster subsystem; simultaneously the environment entropy is much smaller. In the second panel we compute the entanglement entropies in the mean-field critical region $\bar{g} \approx \bar{g}_c$. We find that the system’s entropy growth linearly, the environment entropy remains low, while the entanglement of the cluster phase stays at its initial value, corresponding to the cluster topological phase. The second panel, with $\bar{g} > \bar{g}_c$, shows, in striking contrast with the topological phase, an environment entropy saturating at the same level than the total one, while the cluster is almost only weakly entangled: the system state is therefore random ($\bar{g} \gtrsim \bar{g}_R$).

Random quantum states of a subsystem (or partition of a larger system) may have different entanglement structure depending, for instance, on the size of the environment (or the other partitions). In 2007 Žnidarič et al.¹⁰ noted that the negativity spectrum of a mixed state whose density matrix $R$ is simulated as a superposition of $m$ random pure states $\ket{r_n}$,

$$ \begin{equation} \label{e:m} R = \frac{1}{m} \sum_{n=1}^m \ket{r_n} \bra{r_n}, \end{equation} $$

undergoes a transition between a Marčenko-Pastur like distribution, picked around 0 when $m=1$, to a Wigner semicircular distribution for large $m$. In our context we call $m$ the environment effective number of degrees of freedom, which are necessary to reproduce the value of cluster entanglement witness:

$$ \lambda(\rho_A) = \lambda(R). $$

The effective number of the environment degrees of freedom as seen by the cluster subsystem $m$ as a function of $\bar{g}$. The system size is $2L = 20$. The value of the critical point $\bar{g}_R$ (Markov approximation) is also shown.

This quantitiy is reproduced in the figure as a function of $\bar{g}$, computed for $2L=20$. It shows a sharp growth of the number of degrees of freedom $m$ around the $\bar{g}_R$ predicted by the Markov approximation (note the logarithmic scale). A comparison with the graph $\lambda(\bar{g})$, shows that above $\bar{g}_R$ the cluster entanglement vanishes, coinciding with the multiplication of the environment degrees of freedom; consequently one expect that the negativity entanglement spectrum approaches a semicircular distribution in this parameter region. In this respect, we measure the entanglement spectrum, the set of eigenvalues of $\rho_A$, and the negativity entanglement spectrum, as displayed in the figure below.

Entanglement spectrum (in gray) and negativity entanglement spectrum (pale red) distribution for different values of the coupling between the two subsystems $\bar{g}=0.25,1,2,10$ (left to right, top to bottom panels). The count axis is in a logarithmic scale, to enhance the visibility of the distribution tails. The spectrum is averaged over 64 time steps selected in the stationary long time regime (defined by the saturation of the entanglement entropy).

In the first panel ($\bar{g}<\bar{g}_c$), the entanglement spectrum is essentially the cluster state spectrum with its four degenerated eigenvalues and the remaining zero eigenvalues; in the second panel ($\bar{g} = 1 \gtrsim \bar{g}_c$), the gaps present in the cluster spectrum persist, but become wider, enriching the set of nonvanishing eigenvalues. For $\bar{g} \approx \bar{g}_R$, in the third panel, both spectra are continuous, the gaps of the cluster state disappeared, and the distribution of the negativity spectrum is reminiscent of the Marčenko-Pastur distribution found in Žnidarič et al.,¹⁰ and further studied by Shapourian et al. (2021).¹¹ The last panel shows the thermal state, with a negativity distribution approaching the Wigner semicircular law, for $\bar{g} \gg \bar{g}_c$; deviations with respect to a thermal state appear in the tails of the spectrum distribution.

Spatio-temporal plot of the expected value of the $x$ spin component for both sublattices (even site numbers are for the cluster and odd numbers for the independent spins). (left) $\bar{g} = 1$ (topological phase); (left) $\bar{g} = 10$ (random phase).

Information about the spatial correlations can be obtained from the expected value of the spin operator; by symmetry of the initial state ($\ref{e:ini}$), the $yz$ components remains zero and it is thus enough to follow the $x$-component, as represented in the above figure. We observe that all spins in each sublattices, change simultaneously their magnitude; this is a consequence of the homogeneity of the initial state and the translation invariance of the model, and was used to obtain the relevant Markov equation ($\ref{e:ML}$).

For small values of $\bar{g}$, oscillations of the spin are observed, in accordance with the oscillations of the entanglement entropies. For larger values of $\bar{g}$ relaxation towards a non-magnetic state of the whole system is observed. In the entanglement phase transition region of the first panel, the spins of the cluster and of free lattices are mostly aligned, but tend to alternate at long times; this misalignement between the two sublattices is stronger in the fully random phase of the second panel, for large values of $\bar{g}$. Note that for $\bar{g}=10$, even if the couling is strong, the relaxation is not purely exponential, as happens to be for both $J$ and $g$ large; this is also well explained by the Markov equation, which contains the unitary cluster-field evolution operator.

Topological phase

One defining property of a topological phase is the link between bulk and edge properties. Correlations between edge states are present in a topological phase, even if bulk correlations are short range and vanish exponentially. One possibility to unveil the hiden correlations present in a topological phase, is to measure nonlocal correlation functions, like the expected value of string operators (formed with Pauli matrices) in the quantum state: finite string order parameter means tha the state is topologically nontrivial. In the cluster regime, one expects that the original topology protected by parity extends beyond the neighboring of $g=0$, in spite of the decoherence introduced by the interaction with the independent spins. The appropriated string order parameter in this case is given by

$$ \begin{equation} W(t) = (-1)^L \braket{\psi(t)|Z_1^A Y_2^A \Big( \prod_{x=3}^{L-2} X_x^A \Big) Y_{L-1}^A Z_L^A|\psi(t)}, \end{equation} $$

where we use open boundary condition (to allow for the edge states) and $\ket{\psi(t)}$ is the automaton state at step $t$, and all operators act on the A chain. The cluster state of a periodic chain is the unique ground state of the Hamiltonian ($\ref{e:HC}$); with open edges, the two hanging spins can take any value (labelled by twice the two eigenvalues of $Z$), meaning that the ground state becomes 4-fold degenerated; it is however protected by the parity $\mathbb{Z}_2 \times \mathbb{Z}_2$ symmetry and the energy gap. The string order parameter measures the long range correlation between the two edge qubits, taking into account the partiy linking both (the operator $\prod_x X_x$ in the definition above).

The inital value of the string operator is $W(0)=1$ for the state ($\ref{e:ini}$). It is represented in the figure below.

String order parameter for the cluster subsystem.

We observe that the string order parameter as a function of time step (first panel) quickly reach a stationnary value, in a time much shorter than, for instance, the entanglement entropies, for small $\bar{g}$. Clearly $W$ as a function of $\bar{g}$ displays a transition between a topological phase and a non-topological; it occurs in the range $\bar{g}=(0.5,1)$. The set of curves $W(\bar{g})$ for different system sizes, shows a sharpening of the transition region with increasing size, however we cannot numerically simulate systems much larger. Actually, comparing it with the negativity histograms we may confirm the expectation that, when the spectrum gaps disappear for $\bar{g} \gtrsim 1$, the system becomes trivial.

Conclusion

We investigated how the entanglement properties of a cluster spin chain depend on its exchange coupling with a set of independent spins. By increasing the coupling strength the effective number of the environment degrees of freedom, defined as the number of random states necessary to reproduce the statistical distribution of the cluster’s negativity eigenvalues, we observed a transition between the cluster topological phase, associated to the initial cluster state, to a disordered phase, associated to a random state. The random state itself undergoes an entanglement transition through which the bipartite (system and environment) entanglement entropy increases but the cluster state entanglement disappears, as can be witnessed by the minimum negativity eigenvalue.

Transitions of different random states were already observed in a quantum simulator by Liu et al. (2023)¹²; they varied the respective sizes of a tripartion and observed structural changes in the distribution of the negativity eigenvalues. The subsystem high entanglement phase is consistent with a convolution of Marčenco-Patur distributions (as is our case), while the low entanglement phase shows the usual Wigner distribution.

It would be interesting to implement our automaton in a present day quantum computer³. In particular, the cluster chain coupled with a set of independent spins is a well suited model to be implemented in a gate-based platform using superconducting transmon qubits that natively has a ladder architecture, such as the quantum computer under development within the QSolid project. In addition to provide a relevant test case for such a ladder architecture, it would give us the opportunity to investigate relevant many-body nonequilibrium states, a promising open domain at the interface of quantum matter and information.

Notes

Sellapillay, Kevissen, Laurent Raymond, Alberto D. Verga (2025) Entanglement transition in a cluster spin chain coupled with free spins. arXiv:2501.05937 [quant-ph] ↩
Feynman, Richard P (1982) Simulating Physics with Computers. International Journal of Theoretical Physics 21, 467-88. https://doi.org/10.1007/BF02650179 ↩
Preskill, John. 2023. ‘Quantum Computing 40 Years Later’. In Feynman Lectures on Computation, 2nd ed. CRC Press. ↩↩
Oka, Takashi, and Sota Kitamura (2019) Floquet Engineering of Quantum Materials. Annual Review of Condensed Matter Physics 10, 387-408. https://doi.org/10.1146/annurev-conmatphys-031218-013423. ↩
Kalinowski, Marcin, Nishad Maskara, and Mikhail D. Lukin (2023) Non-Abelian Floquet Spin Liquids in a Digital Rydberg Simulator. Physical Review X 13, 031008. https://doi.org/10.1103/PhysRevX.13.031008. ↩
Kitaev, A. Yu. (2003) Fault-Tolerant Quantum Computation by Anyons. Annals of Physics 303, 2-30. https://doi.org/10.1016/S0003-4916(02)00018-0. ↩
Raussendorf, Robert, Daniel E. Browne, and Hans J. Briegel (2003) Measurement-Based Quantum Computation on Cluster States. Phys. Rev. A 68, 022312. https://doi.org/10.1103/PhysRevA.68.022312. ↩
Fisher, Matthew P.A., Vedika Khemani, Adam Nahum, and Sagar Vijay (2023) Random Quantum Circuits. Annual Review of Condensed Matter Physics 14, 335–79. https://doi.org/10.1146/annurev-conmatphys-031720-030658. ↩
X. Mi et al. (Google team) (2024) Stable quantum-correlated many-body states through engineered dissipation, Science 383, 1332. https://doi.org/10.1126/science.adh9932 ↩
Žnidarič, Marko, Tomaž Prosen, Giuliano Benenti, and Giulio Casati (2007) Detecting Entanglement of Random States with an Entanglement Witness. Journal of Physics A: Mathematical and Theoretical 40, 13787. https://doi.org/10.1088/1751-8113/40/45/017. ↩↩
Shapourian, Hassan, Shang Liu, Jonah Kudler-Flam, and Ashvin Vishwanath (2021) Entanglement Negativity Spectrum of Random Mixed States: A Diagrammatic Approach. PRX Quantum 2, 030347. https://doi.org/10.1103/PRXQuantum.2.030347. ↩
Liu, Tong, Shang Liu, Hekang Li, Hao Li, Kaixuan Huang, Zhongcheng Xiang, Xiaohui Song, Kai Xu, Dongning Zheng, and Heng Fan (2023) Observation of Entanglement Transition of Pseudo-Random Mixed States. Nature Communications 14 (1): 1971. https://doi.org/10.1038/s41467-023-37511-y. ↩

Topological and random phases in a spin ladder1