$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}[1]{\boldsymbol{#1}}$

Talk based on the paper appeared in Phys. Rev. B 107, 085116 (2023), which also contains a complete bibliography. Conference “chats2023” Trends in Hamiltonian systems, chaos and its applications, Luminy, Marseille 2023.

Abstract: We propose a mechanism of dynamical ergodicity breaking driven by the interaction of a cluster spin chain (topological phase) with a chiral particle (quantum walker). The broken ergodic phase is characterized by an emergent magnetic field. We discuss the differences between the near integrable case and the strong interacting one.

Synopsis: One of the challenges in quantum information is to create quantum states that can be used as resources, for instance, in the measurement-based model of quantum computing. Here, I investigate the generation, through a dynamical phase transition, of a topological entangled state, by the Floquet evolution of a chain of spins, whose ground state is the so-called cluster state, acted upon by a quantum walker. The nonergodic phase is characterized by the emergence of magnetic order, persistent at long times.¹

Entanglement transition in the dynamics of the cluster spin chain

Subsystems of an isolated quantum system generically evolve, under a discrete time dynamics driven by a unitary operator (Floquet), towards an equilibrium thermodynamic state of infinite temperature (energy is not conserved). Their entanglement cannot be distinguished from the entanglement of a genuinely random state and as a consequence it cannot be a useful resource for quantum computations. Typical useful states are those ground states associated with a topological phase protected by symmetry and satisfying the area law of the entanglement entropy.

However, even if these states are robust against errors, their entanglement properties degrade rapidly at finite temperature. It is therefore of interest to find nonergodic states, characterized by nonlocal entanglement, at high energy. Here we propose a model, related to the cluster states introduced in the measurement-based quantum computation model, which can evolve towards a highly entangled state through a dynamical quantum phase transition. We investigate the mechanism of ergodicity breaking and the entanglement properties of the asymptotic stationary states.

Cluster dynamical model

We consider a chain of $1/2$-spins

of $L$ sites $x=0,\ldots, L-1$; the hilbert space is spanned by the basis vectors $\ket{s}$, where the integer label $s$ has the binary decomposition $s = s_0 \cdots s_{L-1}$, where $s_x \in \{0,1\}$:

$$\ket{s} = \ket{s_0} \otimes \cdots \otimes \ket{s_{L-1}} = \ket{s_0 \cdots s_{L-1}}.$$

Each spin $x$ of the chain interacts with its neighbors through the exchange of strength $J$

\begin{equation} -J Z_{x-1}X_x Z_{x+1}, \end{equation}

where $\bm \sigma = (X,Y,Z)$ are the pauli matrices. This operator is a stabilizer of the cluster state $\ket{C}$:

\begin{equation} \ket{C} = \frac{1}{2^{L/2}} \prod_x \big(1 + Z_{x-1}X_x Z_{x+1} \big) \ket{0}^L \end{equation}

with $\ket{0}^L$ the tensor product state of $L$ spins up ($s=0\cdots0 = 0$). Moreover, $\ket{C}$ is the ground state of the “cluster” Hamiltonian

\begin{equation} H_C = - \frac{J}{2} \sum_x Z_{x-1}X_x Z_{x+1} \end{equation}

a topological phase protected by the $\mathbb{Z}_2 \times \mathbb{Z}_2$ symmetry (generated by the string operators $\prod_x X_x$, with $x$ odd and even). In addition to the exchange interaction each spin is subject to an external field $B$ in the $x$ direction

\begin{equation} H_B = - \frac{B}{2} \sum_x X_x. \end{equation}

The cluster model, associated with the $H_C+H_B$ hamiltonian, describes a system that undergoes a quantum phase transition when varying the external field from zero (the cluster state) to $B>J$ (the paramagnetic state). The cluster state (whose magnetization is zero) differs from the paramagnetic state in its entanglement properties. The cluster state satisfies the area law of the entanglement entropy. It is a topological phase protected by symmetry, excitations are separated from the ground state by an energy gap. These properties make the cluster state an interesting resource of quantum information, and it is the base of the so called “measurement based quantum computation”.

Instead of considering the hamiltonian system $H_C+H_B$, whose ground state is precisely $\ket{C}$, we impose a discrete time dynamics generated by the floquet unitary $F(J,B)$

\begin{equation} \ket{\psi(t+\Delta t)} = F(J,B) \ket{\psi(t)}, \quad F(J,B) = \E^{- \I H_C \Delta t} \E^{- \I H_B \Delta t} \end{equation}

where $\ket{\psi(t)}$ is the system’s state at time $t \in \mathbb{Z}$, and the time interval $\Delta t = 1$ is our unit of time (we also choose $\hbar = 1$); note that $H_B$ do not commute with $H_B$.

The dynamics generated by $F(J,B)$ is completely integrable, as can be shown using the Jordan-Wigner transformation It is defined by

\begin{equation} \begin{split} X_x &= 1 - 2 f^\dagger_x f_x, \\ Y_x &= \I K_x (f^\dagger_x - f_x), \\ Z_x &= -K_x (f^\dagger_x + f_x), \end{split} \label{e:JW} \end{equation}

where

\begin{equation} \label{e:Kff} K_x = \prod_{y=0}^{x-1} \E^{\I \pi f^\dagger_y f_y} = \prod_{y=0}^{x-1}( 1 - 2 f^\dagger_y f_y ). \end{equation}

and

\begin{equation} \label{e:ff} \{f_x,f_y\} = \{f_x^\dagger,f_y^\dagger\}, \quad \{f_x,f_y^\dagger\} = \delta_{xy}. \end{equation}

are the commutation relations of the fermion annihilation and creation operators.

This transformation, together with a fourier transform (the system is translation invariant), leads to the effective hamiltonian $H_F = \I \ln F$ representation of the floquet operator:

\begin{equation} \label{e:HF} H_F = -\sum_k C^\dagger h_k C_k, \quad C_k = \begin{pmatrix} f_k \\ f^\dagger_{-k} \end{pmatrix}, \end{equation}

where

\begin{equation} \label{e:hk} h_k = \epsilon_k \bm n_k \cdot \bm \sigma , \end{equation}

$\epsilon_k$ gives the energy bands (figure below)

\begin{equation} \label{e:ek} \cos(\epsilon_k) = \cos J \cos B - \sin J \sin B \cos 2k; \end{equation}

and the unit vector

\begin{equation} \label{e:nk} \bm n_k = \frac{1}{\big| \sin \epsilon_k \big|} \begin{pmatrix} \sin J \cos B \sin 2k \\ \sin J \sin B \sin 2k \\ \sin J \cos B \cos 2k + \cos J \sin B\end{pmatrix} \end{equation}

whose rotation gives the winding number $\nu$. The winding number characterize the topology of the energy bands.

Energy bands and topology of the integrable cluster system

An exact calculation gives the evolution of the initial all $\ket{+}$ spins state:

\begin{equation} \label{e:0t} \ket{t} = \prod_k \big[ \cos(\epsilon_k t) + \I n_z(k) \sin(\epsilon_k t) + \I n_-(k) \sin(\epsilon_k t) f_{-k}^\dagger f_k^\dagger \big] \ket{0} . \end{equation}

at time $t$, where $n_\pm = n_x \pm \I n_y$, and $\bm n = (n_x, n_y, n_z)$. Therefore, we can compute the Loschmidt echo ratio $\lambda(t)$ and the multipartite entanglement measure $\mathcal{Q}(t)$.

Quasi-energy bands as a function of the exchange $J$ and wavenumber $k$ for a fixed field $B = 1.1$. For $J=B$ dirac points appear, signaling the possibility of phase transitions.

It is straightforward to demonstrate that the effective hamiltonian supports chiral modes, in particular there exists a gauge vector potential that allows $H_F$ be written in explicit chiral form. Using this form one may compute exactly the winding number of the energy bands, as shown in the figure below.

In the $(J,B)$ plane the lines $J=\pm B$ separate trivial to topological phases, as measured by the value of the electronic bands winding number (here associated to the effective hamiltonian).

To analyse the dynamics of the phase transition between the $J < B$ and $J > B$ cases, we introduce the loschmidt ratio,

\begin{equation} \label{e:lambda} \lambda(t) = - \frac{1}{L} \ln \mathcal{L}(t) , \quad \mathcal{L}(t) = |\braket{0 | t}|^2 , \end{equation}

which is an intensive quantity (it has a finite limit when the size of the system tends to infinity); it is related to the Loschmidt echo, which measures the overlap between the initial and evolved states. The loschmidt ratio presents singularities at the dynamical phase transitions.

In analogy with the thermodynamic free energy, the singularities of the loschmidt ratio evidence dynamical transitions. When $J>B$ the initial product state evolves towards a highly entangles state through a dyanamical phase transition.

The dynamical transition characterize by different entanglement levels. For $B>J$ the entanglement remains weak, in accordance with the absence of transitions.

\begin{equation} \label{e:Qpure} \mathcal{Q}(t) = 2 - \frac{2}{L} \sum_{x=0}^{L-1} \Tr \rho^2_x(t) = 1 - \frac{1}{L} \sum_x \braket{\psi(t)|\bm \sigma_x |\psi(t)}^2, \end{equation}

Spin-particle interaction

A natural question arises about the fate of the (dynamical) cluster state when integrability is broken. Is it possible to generate useful entangled states in the case of a chaotic dynamics? Is it possible to obtain at high energy nontrivial topological states, even when the external field is larger than the exchange coupling?

To answer these questions we modify the cluster model by adding a particle (like a quantum walker) that, jumping from site to site, exchanges its spin with the fixed spins of the chain. One interesting aspect of this modification is that it adds to the well localized spin degrees of freedom the delocalized degrees of freedom of a particle (the support of the particle wave function naturally extends to the whole system). The second important property of the modified model is that it preserves, with a good choice of the particle-spin interaction, the original symmetries of the cluster model. This is essential to ensure the possible existence of nontrivial topological phases, protected by the same symmetries as the ones of the cluster state.

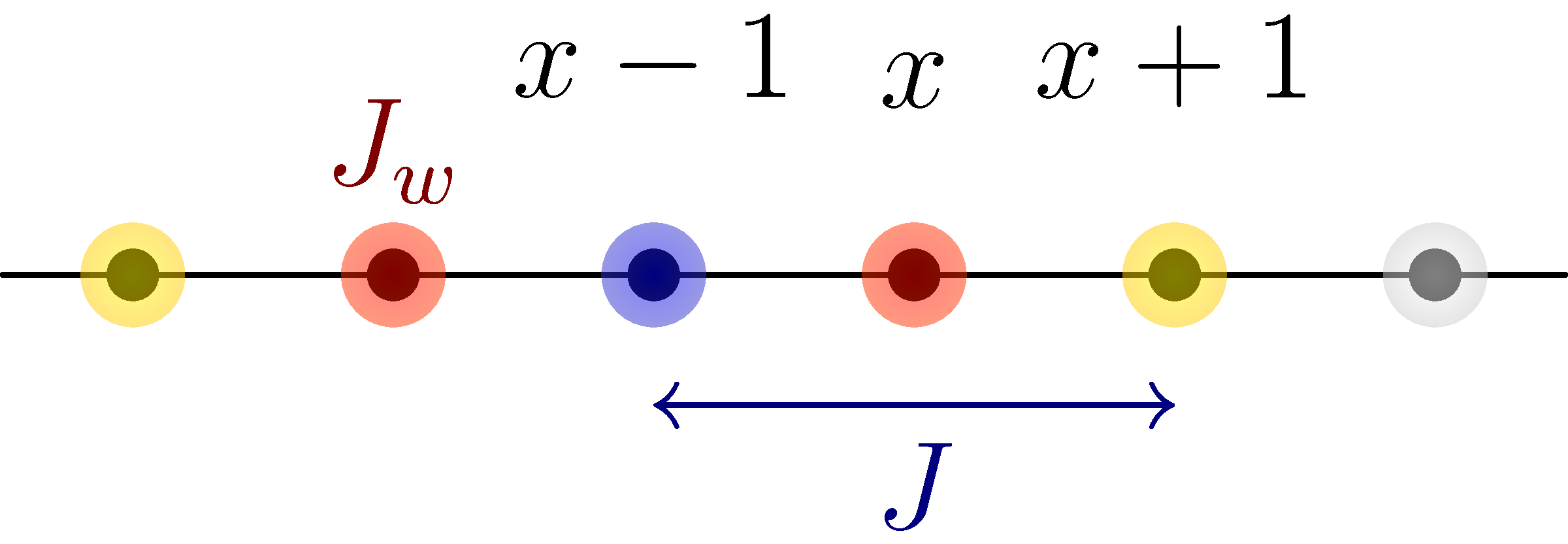
The original chain ($J$) is modified by the presence of a jumping particle (the colors around each site represent the particle position distribution), which in addition, exchange ($J_w$) its internal spin (coin value) with each spin of the chain. The particle creates an “environmnet” around the fixed spins.

The presence of the walker leads to an enlarged hilbert space: a basis vector has now the form

\begin{equation} \label{e:xcs} \ket{xcs} = \ket{x} \otimes \ket{c} \otimes \ket{s} \in \mathcal{H}, \quad x \in \{0,\ldots,L-1\}, \\ c \in \{0,1\}, \; s \in \{0,\ldots,2^L-1\} , \end{equation}

where $x$ and $c$ are the position and spin (or “coin”) of the particle, and $s$ is as before, the set of fixed spins.

The particle-spin interaction is defined by

\begin{equation} \label{e:Jex} W_x(J_w) = \exp\big( \I J_w \tau^{(x)} X_x\big) , \end{equation}

where $J_w$ is the coupling energy, and $\bm \tau$ the pauli coin operator. The fact that it depends only on the $X$ spin component, ensures that the $\mathbb{Z}_2 \times \mathbb{Z}_2$ symmetry is preserved. The new floquet operator is

\begin{equation} \label{e:Fqw} F_\text{QW} = F(J,B)W(J_w)MC(\theta) , \end{equation}

where $M$ (motion) is the particle shift operator $x \rightarrow x+1$, and $C$ (coin) rotates the particle spin by an angle $\theta$ around the $x$ axis. The combined operator $MC(\theta)$ corresponds to the quantum walk of a particle on the line, whose continuum limit gives the Dirac equation (with a $\theta$ dependent effective mass): when $\theta \approx \pi/2$ the group velocity of the particle is near its phase velocity of 1, while when $\theta\approx \pi/4$ the group velocity is much smaller than the phase velocity, increasing the effect of dispersion.

Our task now is to generalize the loschmidt and entanglement measures to the mixed state case. Indeed, the addition of the walker transform the spin chain into an “open” system, whose hilbert space is a subspace of the total (particle plus spin) hilbert space. The spin subsystem is then described by the reduced density matrix

\begin{equation} \label{e:rhos} \rho_s(t) = \Tr_{xc} \rho(t), \; \rho(t) = \ket{\psi(t)} \bra{\psi(t)} , \end{equation}

where $\ket{\psi(t)}$ is the state that has evolved from the initial $\ket{\psi(0)}$ state,

\begin{equation} \label{e:Fpsi0} \ket{\psi(t)} = F_\text{QW}^t \ket{\psi(0)} . \end{equation}

The loschmidt ratio is defined in terms of the spin density matrix (instead of the spin state),

\begin{equation} \label{e:peres} \mathcal{L}_s(t) = \frac{\Tr \rho_s(0) \rho_s(t)}{\Tr \rho_s(0)^2} ,\quad \lambda_s(t) = - \frac{1}{L} \ln \mathcal{L}_s(t) , \end{equation}

and the multipartite entanglement is given by the local (dependent on the lattice site) spin density matrix

\begin{equation} \label{e:Qmix} \mathcal{Q}_s(t) = \frac{1}{L} \sum_{x=1}^L \tau_s(x,t), \quad \tau_s(x,t) = 4 \det \rho_s(x,t), \end{equation}

where $\tau_s$ is the so called one-tangle, and

$$\rho_s(x,t) = \Tr_{\bar{s}_x}\rho_s(t), \quad \bar{s}_x = s_1 \ldots s_{x-1} s_{x+1} \ldots s_L$$

is the one spin density matrix. This quantity is related to the expected value of the $X$ magnetization.

One may think the influence of the particle as an effective magnetic field which adds to the already present external $B$, or, depending on the localization of the particle, as a source of decoherence of the spin subsystem, which can eventually lead the spin chain to a thermal state.

Near integrable case

We first observe that the dynamical phase transition toward a topological entangled phase we analysed in the integrable case, is also present in the interacting spin-particle system. When both $(J,B)$ are small, the discrete time dynamics tends to a continuous time evolution associated with the combined spin-chain and walker hamiltonians.

A rather interesting new effect is the interaction induced localization of the particle around its initial position, depending on the spin chain parameters (figure).

Square of the particle wave function and spin tangle in the near integrable case. (a) $J=0.03$, $B=0.01$; (b) $J=0.01$, $B=0.03$.

We observe localization of the walker when $J>B$, and strong spatial fluctuations of the entanglement. In fact the tangle $\tau(x,t)$ reflects the behavior of the $x$-magnetization. In the integrable case a strong magnetization signals a near product unentangled state. In contrast, here an emergent magnetization is correlated with an entangled state. This property is also present in the strong interacting case.

Loschmidt ratio and entanglement comparison between $J>B$ (a) and $J<B$ (b) cases (parameters as in the previous figure).

In analogy with the integrable case, we find a highly entangled phase that follows a dynamical phase transition, as probed by $\lambda(t)$, which shows a kink (taking into account that the number of spins is $L=14$, one may not expect a neat singularity).

Strongly interacting regime

The behavior of the system in the strongly interacting case is very rich, and many different regimes are observed depending on the four parameters $J,B,J_w$ and $\theta$. First, the “normal” behavior of relaxation to a thermal state is found in the case $B>J$ and strong particle coupling $J_w \approx \pi/2$, where the interaction is essentially a swapping between the coin and the spin (figure below).

Thermal state obtained in the strong coupling regime $J_w =1.5$, $\theta=\pi/4$, and $(J,B)= (0.2,0.6)$. (a) Subsystem entropy of the $x$, $c$ and $s$ degrees of freedom; (b) loschmidt ratio of the spin subsystem; (c) von Newmann entropy of partition A with $L/2$ spins (half system); (d) multipartite entanglement of the spin subsystem.

In this case the entanglement rapidly grows toward its maximum value, corresponding to a random quantum state. In particular the von Newman entropy

$$\mathcal{S}[\rho] = -\Tr \rho \log \rho$$

which is a functional of the density matrix ($\log$ is base 2), for the different subsystems, $\{x,c,s\}$ and half-chain $x \in A$, saturates to its maximum equal probability value. At the same time the $x$-magnetization tends to zero: the reached thermal state is paramagnetic. It is worth noting that the remnant magnetization even smaller than the corresponding to the applied field which confirms the ability of the walker to randomize the spin chain.

Non-thermal state obtained in the $J<B$ case for a spin-particle coupling $J_w = 0.5$. Panels (a-d) as in the previous figure.

Second, we find a dynamical transition towards a highly entangled state and finite magnetization, in the $J<B$ case “balanced” spin-particle coupling $J_w = 0.5$, which is impossible without the interaction with the walker (figure above). Here, the remarkable point is that the observed magnetization cannot be solely explained by the applied field, which would lead to a trivial paramagnetic phase of negligible entanglement. On the contrary, the emergent magnetization is here correlated with a highly entangled state.

Particle motion (position probability distribution) (a), and magnetization distribution (b) in the non-thermal case with $J<B$ and $J_w=0.5$.

This emerging magnetization is in fact a measure of the ergodicity breaking associated with the system’s dynamics. Moreover, in contrast to the thermal state, persistent spatial fluctuation remain at long times (figure above).

Another important difference between the integrable (I), non-thermal (NT), and thermal (T) cases, is related with the way entanglement grows. While the usual area (rapid saturation) and volume (ballistic) laws are followed by I and T, the nonergodic NT regime is characterized by a logarithmic entanglement growth law, as observed in same critical quantum random networks (at the separation of the area to volume transition).

Conclusion

We showed that an isolated quantum system subject to a discrete time dynamics can evolve to a chaotic state different to a thermal state, characterized by a finite magnetization and high entanglement. Ergodicity breaking and its associated dynamical entanglement transition are driven only by unitary transformations, in which a particle (quantum walker) plays the role of the environment to the spin chain.

Notes

Verga, A.D. Entanglement dynamics and phase transitions of the Floquet cluster spin chain Phys. Rev. B 107, 085116 (2023) arXiv:2208.01706, and references therein. ↩