$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \DeclareMathOperator{\Tr}{Tr} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}{\boldsymbol}$

Lectures on advanced quantum mechanics

Entanglement measures

von Neumann entropy

A composite system in a pure state is disentangled if it can be factored into a product of states:

$$ \ket{\psi} = \ket{\psi_1}\ket{\psi_2} \ldots, \quad \ket{\psi}\in \mathcal{H} = \mathcal{H}_1 \otimes \mathcal{H}_2 \ldots $$

and $\ket{\psi_n} \in \mathcal{H}_n$.

The von Neumann entropy $S(\rho)$ of a state $\rho$ is a measure of entanglement of a subsystem belonging to a system in a pure state, whose reduced density matrix is precisely $\rho$; if $p_1, p_2, \ldots$ is a set of eigenvalues of $\rho$, then $S$ coincides with the Shannon entropy of the distribution $p_n$:

$$ S(\rho) = -\sum_n p_n \log p_n\,. $$

The “neumann” entropy accounts then for the entanglement of a pure bipartite state, and $p_n$ are the schmidt decomposition coefficients (see the qubit lecture). Note that the neumann entropy is not a good measure of the entanglement of a mixed state; for instance, the reduced density matrices of qubit $A$ corresponding to the states $\rho_e$ and $\rho_d$ are the same, but one is entangled and the other not. For general (bipartite) mixed states one must distinguish the contribution of classical correlation from the quantum ones.

The neumann entropy fulfills a set of requirements that any entanglement measure $Q$ should satisfy:

For pure states $\rho = \ket{\psi} \bra{\psi}$, the entanglement measure is the von Neumann entropy
$$ Q(\rho) = S(\rho_A) $$
with $\rho_A$ the reduced density matrix of part $A$.
A separable state $\rho_d$ has zero entanglement $Q(\rho_d) = 0$.
The entanglement of independent systems $\rho = \rho_A \otimes \rho_B$ is additive
$$ Q(\rho) = Q(\rho_A) + Q(\rho_B)\,. $$
$Q$ is invariant under unitary transformations
$$ Q(\rho) = Q(U \rho U^\dagger)\,. $$
$Q$ is convex:
$$ Q\left(\sum_n p_n \rho_n\right) \le \sum_n p_n Q(\rho_n)\,. $$

As a consequence, local measurements cannot increase the average entanglement

$$Q(\ket{\psi_{AB}}) \ge \sum_n p_n Q(\ket{\psi_n})\,,$$

where

$$p_n = \braket{\psi_{AB}| P^A_n |\psi_{AB}}$$

is the probability of a measure of the property $n$ of the $A$ part, and

$$\ket{\psi_n} = \frac{P^A_n \ket{\psi_{AB}}}{\sqrt{p_n}}$$

is the corresponding state of $AB$. In a similar way, throwing away part of a system, cannot increase its entanglement.

Negativity

Contrary to the case of pure states, where the von Neumann entropy is a well defined entanglement measure, the quantification of the entanglement of general mixed states is more ambiguous. A mixed state of a bipartite system $AB$ that can be written as

$$ \rho_{AB} = \sum_n p_n \rho_n^A \otimes \rho_n^B $$

is separable, and its state is said to be disentangled. A separable state contains, in general, only classical correlations betweens its two parts, in the sense that they do not provide a quantum advantage for quantum computing.

Consider the case of two qubits $AB$ Bell state:

$$ \rho_e = \ket{\Phi_+} \bra{\Phi_+}, $$

which is a fully entangled pure state, and the mixed state formed by two Bell states:

$$ \rho_d = \frac{1}{2} \ket{\Phi_+} \bra{\Phi_+} + \frac{1}{2} \ket{\Phi_-} \bra{\Phi_-} $$

which, at variance to $\rho_e$, is disentangled: it is a mixture of two maximally entangled states, and can be written in the separable form,

$$ \rho_d = \frac{1}{2} \ket{00}\bra{00} + \frac{1}{2} \ket{11}\bra{11}\,, $$

resulting in a state without quantum correlations between A and B. In fact, any equal mixture of maximally entangled states is separable. A remark is in order, the entanglement entropy of a separable state $S(\rho)$, thought as a subsystem of a pure state whole system, is not zero: it is the entanglement between its two parts, entanglement that cannot be measured by the von Neumann entropy, which vanishes. A suitable measure of a partition of a mixed state is the negativity, we define below.

It is easy to show that, for a separable state,

$$ \rho_A = \Tr_B \rho_d = \sum_n p_n \rho^A_n, \quad \rho_B = \Tr_A \rho_d = \sum_n p_n \rho^B_n, $$

are the states of $A$ and $B$, respectively. For the case of the two maximally entangled states, we obatqin EX:

$$ S(\rho_d) = S_{AB} = 2, \; S_A = 2, \text{ and } S_B = 2, $$

which is a particular case showing the subadditivity property of the entropy:

$$ S(\rho_{AB}) \le S(\rho_A) + S(\rho_B). $$

The difference of these two combinations $AB$, and $A$ and $B$, defines the mutual information

$$ I(A:B) = S_A + S_B - S_{AB} \ge 0, $$

which is always positive, and measure the amount of information on $B$ we can gain knowing the state $A$, or vice-versa. We obtain, in the example, $I = 2 = S_B$, which coincides with the classical limit (the classical mutual information cannot excedd the Shannon entropy of one of its parts). We verity that, for a pure state, the maximum is $I = 2S_A$.

A necessary condition for a state $\rho \in \mathcal{H}_A \otimes \mathcal{H}_B$ to be separable, is the positive partial transpose or Peres criterion:

$$ \rho^{T_B} \ge 0 $$

where $T_B$ is the transposition in the $B$ subspace of $\mathcal{H}$:

$$ \rho_{k_A m_B;l_A n_B}^{T_B} = \rho_{k_A n_B, l_A m_B}\,. $$

A separable state satisfies the peres criterion trivially:

$$ \rho^{T_B}= \sum_n p_n \rho_A \otimes \rho_B^T, \quad \rho_B^T \ge 0 $$

because the transpose of a positive matrix is positive, thus $\rho^{T_B} \ge 0$.

A measure of mixed states entanglement, based on the Peres partial transpose, is the negativity. We partition into two parts A and B a system in the state $\rho$, and compute the partial transpose

$$ \bar{\rho}_A = \rho^{T_B}, \quad \mathrm{dim} \rho = \mathrm{dim} \bar{\rho}_A $$

and its spectrum $\lambda_n$; the logarithmic negativity is defined by

$$ N_A = -\log \sum_{n} |\lambda_n|, \quad \lambda_n \in \mathrm{spec} \big(\bar{\rho}_A\big) . $$

It is worth noting that in general the eigenvalues of the partial transposed density matrix can be negative; in the case where $\lambda_n \ge 0$ for all $n$, the negativity vanishes, and the corresponding state is separable. In our example of maximally entangled states, forming a mixed separable state, it straightforward to verify that the negativity vanishes.

Entanglement formation and distillation

In order to define a mesure of mixed state entanglement one may use the maximally entangled states as a unit of entanglement (the bell states in the case of two qubits), and compare the mixed state with an equivalent number of such states. For example, given set of maximally entangled states, we may evaluate the number and probabilities we must chose to build a mixed state; this operation allows us to define an entanglement of formation measure:

$$Q_F(\rho) = \min \sum_n p_n S(\rho^A_n)$$

where

$$\rho =\rho_{AB} = \sum_n p_n \ket{\psi_n} \bra{\psi_n},\; \rho_n^A = \Tr_B \left( \ket{\psi_n} \bra{\psi_n} \right)\,,$$

$\ket{\psi_n}$ a set of maximally entangled states in $AB$, and $S$ the neumann entropy.

Distillation is the inverse processes: given a mixed state we must determine the set of maximally entangled state we can obtain.

Distillation of a not maximally two qubits state $\ket{\psi}$ into a maximally entangled bell state $\ket{\Phi_+}$. The distillation of entanglement measure $Q_D$ is the ratio of $M$ copies of $\ket{\psi}$ that can be converted, using local measurements, into $N$ bell states $\ket{\Phi_+}$. The bell state is then a unit of entanglement:
$$Q_D(\ket{\psi}) = \lim_{M \rightarrow \infty} \frac{N(M)}{M}$$
The entanglement of formation measure, is instead given by the ratio $N$ maximally entangled states necessary to obtain $M$ not maximally entangled states
$$Q_F(\ket{\psi}) = \lim_{M \rightarrow \infty} \frac{N}{M(N)}$$

Let us present a simple example of distillation of a pure state. We want to obtain the bell state $\ket{\Phi_+}$ from the not maximally entangled pure state,

$$\ket{\psi_{AB}} = \cos \theta \ket{00} + \sin \theta \ket{11}$$

We proceed as follows, we add an ancilla $A'$ in state $\ket{0}$, to get

$$\ket{\psi_{A'AB}} = \ket{\psi} = \cos \theta \ket{000} + \sin \theta \ket{011}\,,$$

and apply the unitary operator $U$ on the first two qubits:

$$U\ket{00x} = \tan \theta \ket{00x} + (1 - \tan^2 \theta)^{1/2} \ket{10x}$$

amd

$$U\ket{01x} = \ket{01x}$$

Therefore EX,

$$U \ket{\psi_{A'AB}} = \sqrt{2} \sin \theta \ket{0}_{A'} \otimes \ket{\Phi_+} + (1 - 2\sin^2 \theta)^{1/2} \ket{1}_{A'} \otimes \ket{10}\,,$$

if the measure of the ancilla qubit gives the state $\ket{0}$, the $AB$ state is just the bell state; in the other case, we repeat the procedure: the success probability is $p(\theta) = (1/2) 2 \sin^2(\theta)$, and after $N$ steps the number of distilled maximally entangled states is $Np(\theta)$. We observe that the distillation protocol concentrates the entanglement, while its inverse, the formation protocol, dilutes the entanglement.

The relative entropy

$$S(\rho \parallel \sigma) = \Tr \rho \log \frac{\rho}{\sigma} \ge 0$$

can be used as a measure of entanglement:

$$Q(\rho_{AB}) = \min_{\sigma \in \mathcal{S}} S(\rho_{AB} \parallel \sigma)$$

where $\mathcal{S}$ is the set of disentangled states $\sigma \sim \sigma_A \otimes \sigma_B$. The relative entropy is a distance measure from the (convex) set of separable states. The separable state $\sigma$ that realizes the minimum of the relative entropy, is the best separable approximation of the entangled state $\rho_AB$. The relative entropy of entanglement gives an upper bound of the entanglement of distillation; as a consequence, and taking into account that

$$Q(\rho) \le Q_F(\rho)$$

we find that the entropy of distillation is in general smaller than the corresponding entropy of formation; this can be interpreted as a result of the irreversibilty of the measurements used to build the mixed state from the set of maximally entangled ones.

An useful generalization of the von Neumann entropy is the Rényi entropy, that can also be used as a measure of entanglement:

$$S_q(\rho) = \frac{1}{1-q} \log \Tr \rho^q$$

where $q=0,1$, or $q>1$; for $q=0$ the rényi entropy $S_0$ is proportional to the rank of the corresponding hilbert space; for $q = 1$ it is the neumann entropy $S_1 = S$; the rényi entropy has most of the $S$ properties, but the subadditivity. Note that for $q=2$ we have

$$S_2(\rho) = - \log \Tr \rho^2$$

which is a straightforward measure of the purity. An experimental protocole to measure the $S_2$ entropy of a subsystem, was recently introduced; it is based on random measurements of the configurations of a spin chain, physically implemented by a set of unitaries.¹

Concurrence

In the case of two qubits a complete characterization of the entanglement of formation is possible using the concurrence $C$. The concurrence, although related to an entanglement measure, it is not itself a proper measure.

We consider first a one qubit state

$$\ket{\psi} = a \ket{0} + b \ket{1}$$

and construct an orthogonal state

$$\ket{\bar{\psi}} = YK \ket{\psi}$$

where $K$ is the operator of complex conjugation:

$$K \ket{\psi} = \ket{\psi^\star} = a^\star \ket{0} + b^\star \ket{1}\,,$$

and,

$$Y\ket{\psi^\star} = - \I b^\star \ket{0} + \I a^\star \ket{1}\,,$$

leading to,

$$\braket{\psi | \bar{\psi}} = 0\,.$$

We remark that the operator $YK$, like the time reversal operator, change the sign of the pauli matrices $K^\dagger Y \bm \sigma YK = - \bm \sigma$. The concurrence of such state is always zero:

$$C(\ket{\psi}) = |\braket{\psi | \bar{\psi}}| = 0$$

In the case of two qubits the generalization

$$\ket{\bar{\psi}_{AB}} = Y \otimes Y \ket{\psi^\star}, \, \ket{\psi^\star} = K \ket{\psi},$$

do not lead to orthogonality, except if it is a product state. Indeed, using the schmidt decomposition,

$$\ket{\psi_{AB}} = \sum_{n=1}^2 \sqrt{p_n} \ket{n_A} \otimes \ket{n_B}$$

one finds EX,

$$C(\ket{\psi_{AB}}) = |\braket{\psi_{AB} | \bar{\psi}_{AB}}| = 2 \sqrt{p_1 p_2}\,.$$

For a general mixed state $\rho$, we define,

$$\bar{\rho} = (Y\otimes Y) \rho^\star (Y\otimes Y)$$

is the spin flipped state, and the concurrence ²,

$$C(\rho) = \max \{0, \lambda_1 - \lambda_2 - \lambda_3 - \lambda_4 \}$$

where $\lambda_n$ are the four eigenvalues of the hermitian matrix

$$\sqrt{\sqrt{\rho} \bar{\rho} \sqrt{\rho}}$$

sorted in decreasing order. Equivalently, the matrix,

$$\rho \bar{\rho}\,,$$

which although not hermitian is positive, has positive eigenvalues whose square roots correspond to the same $\lambda_n$ ($n=1,2,3,4$).

In addition, as we said before, the concurrence is related with the entanglement entropy of formation. In the case of a pure state we have,

$$Q_F(\ket{\psi}) = H\left( \frac{1 + \sqrt{1-C(\ket{\psi})^2}}{2} \right)$$

where

$$H(p) = -p \log p - (1-p) \log (1-p)$$

is the binary shannon entropy, and for a mixed state a similar formula holds,

$$Q_F(\rho) = H( C(\rho))\,.$$

The concurrence measures then the entanglement formation of two qubits, which is based on the spin flip operator

$$\mathcal{I}_2: \rho \rightarrow \bar{\rho} = \frac{1}{2}(1_2 - \bm r \cdot \bm \sigma)\,,$$

where $\rho = (1 + \bm r \cdot \bm \sigma)/2$. It can be generalized by generalizing the inversion operator $I_D = I_A \otimes I_B$ to a system of larger dimension $D = D_A \times D_B$ in a bipartite pure state $\ket{AB}$:

$$C(\ket{AB}) = \sqrt{ \bra{AB} I_D (\ket{AB}\bra{AB})\ket{AB} }$$

where

$$I_D (\rho_{AB}) = \nu_A \nu_B \left( 1_A \otimes 1_B - \rho_A \otimes 1_B - 1_A \otimes \rho_B + \rho_{AB} \right)\,,$$

with $\nu_A = 1/(D_A - 1)$ and $\nu_B = 1/(D_B - 1)$; or equivalently,

$$C_D(\rho) = \sqrt{2 \nu_A \nu_B(1 - \Tr \rho_A^2)}\,.$$

Exercises

Show that the state
$$\rho = \frac{1}{4} (1-p) 1_4 + p \ket{\Psi_-} \bra{\Psi_-}$$
($\ket{\Psi_-} = (\ket{01} - \ket{10})/\sqrt{2}$) is entangled (not separable) for $p>1/3$.
Show that
$$\bar{\rho} = Y \rho^\star Y = \frac{1_2 - \bm r \cdot \bm \sigma}{2}$$
if
$$\rho = \frac{1_2 + \bm r \cdot \bm \sigma}{2}$$
Deduce the concurrence formula $\rho = \ket{\psi} \bra{\psi}$,
$$C(\rho) = \sqrt{\Tr (\rho \bar{\rho})} = |\braket{\psi | Y \otimes Y | \psi^\star}$$
Entanglement sudden death.³ We consider two independent two level atoms $A$ and $B$ in a photon cavity; the interaction with the photons entangles the atoms. In 2004 Eberly and coworkers studying the decoherence of an initial entangled state, discovered that disentanglement by the environment can be effective in a finite time.

The problem can be reduced to the lindblad equation for the two atoms, taking as collapse operators (as are referred the lindablad operators in quantum optics) the phase damping $\sigma_-^A$ and $\sigma_-^B$:
$$\frac{\D}{\D t}\rho(t) = \frac{\nu}{2} \left[ \mathcal{L}(\sigma_-^A,\rho) + \mathcal{L}(\sigma_-^B,\rho) \right]$$
where,
$$\mathcal{L}(\sigma,\rho) = 2 \sigma \rho \sigma^\dagger - \sigma^\dagger \sigma \rho - \rho \sigma ^\dagger \sigma\,.$$
- Solve the lindblad equation for the initial condition
  $$\rho(0) = \frac{1}{3}\begin{pmatrix} x & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 1 - x \end{pmatrix}$$
  where $x \ge 0$. You may write the solution in the form
  $$\rho(t) = \frac{1}{3}\begin{pmatrix} a(t) & 0 & 0 & 0 \\ 0 & b(t) & d(t) & 0 \\ 0 & d(t) & c(t) & 0 \\ 0 & 0 & 0 & 3 - a(t) - b(t) - c(t) \end{pmatrix}$$
  and solve the set of differential equation for the unknowns $a,b,c$ and $d$.
- Using the previous solution find the concurrence:
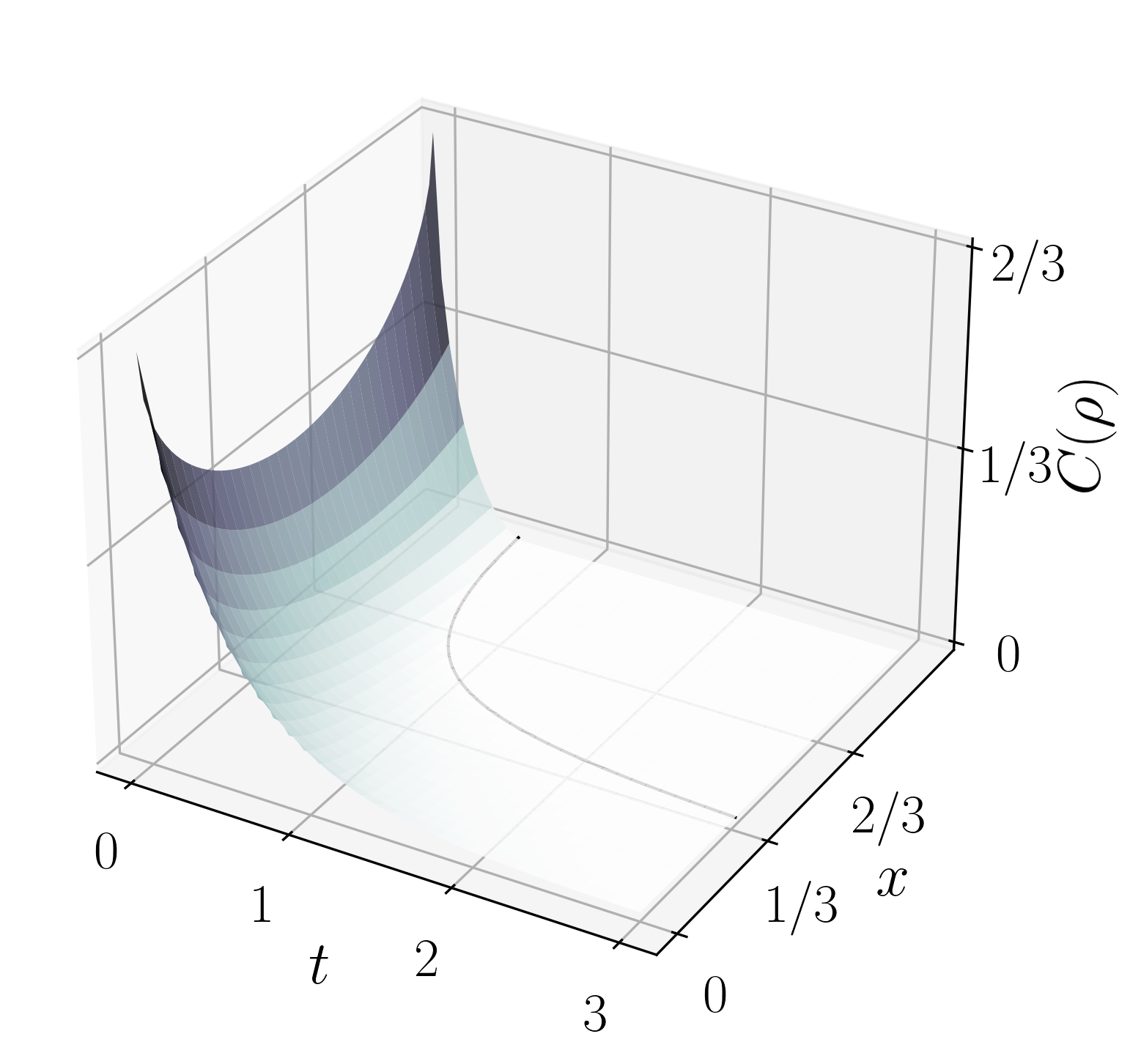
  $$C(\rho) = \max\left\{0, \frac{2 \E^{-\nu t}}{3} \left[1 - \sqrt{x \big(3 -2 \E^{-\nu t}(1+x) + \E^{-2\nu t}x \big) } \right] \right\}\,.$$
- Plot the concurrence as a function of time, for $x \in (0,1)$. Discuss the result.

Concurrence as a function of time and $x$, a parameter characterizing the quantum state $\rho_x(t)$. The solid line separates the region where the entanglement vanishes: for a range of $x$ values the entanglement death time is finite.

Notes

A thorough discussion of the entanglement measure can be found in the paper:

Plenio, M., and Virmani, S., An introduction to entanglement measures, arXiv:quant-phys/0504163 (2005) .pdf

Brydges et al., Probing Rényi entanglement entropy via randomized measurements, Science 364, 260 (2019) .pdf ↩
Wooters, W., Entanglement of Formation of an Arbitrary State of Two Qubits, Phys. Rev. Lett. 80, 2245 (1998) ↩
Ting Yu, and Eberly, J., Finite-Time Disentanglement Via Spontaneous Emission, Phys. Rev. Lett. 91, 140404 (2004) .pdf ↩