$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \DeclareMathOperator{\Tr}{Tr} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}{\boldsymbol}$

Lectures on advanced quantum mechanics

Qubit: the quantum of information

There is a deep difference between the classical unit of information and its quantum counterpart. A qubit corresponds to the state of a quantum system having two levels (a hilbert space of dimension 2); therefore, the qubit is physical. A bit, or binary digit, is related to a logical state, true or false; its physical implementation as a system having two equilibrium states, is not essential in its definition.

In 1995, Schumacher¹ demonstrated the quantum version of the noiseless coding theorem of Shannon (see the lecture on classical information). He showed that the von Neumann entropy is the mean number of qubits necessary to encode the states of an ensemble or composite quantum system. Therefore, a quantum state carries an amount of information that can be measured using the von Neumann entropy.

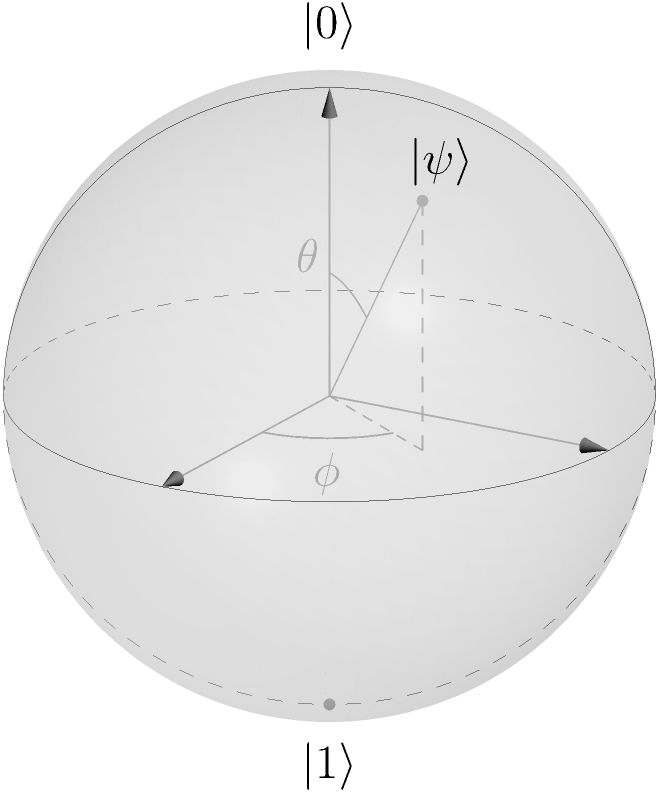
A general qubit, a two-dimensional ket $\ket{\psi} \in \mathcal{H}$ ($\mathrm{dim} \mathcal{H} = 2$), can be written using the spherical polar $\varphi \in (0,2\pi)$ and azimuth $\theta \in (0,\pi)$ angles:

$$\ket{\psi} = \cos \frac{\theta}{2} \ket{0} + \E^{\I \varphi} \sin \frac{\theta}{2} \ket{1}$$

where $\{\ket{0}, \ket{1}\}$ is the canonical basis of $\mathcal{H}$. This representation identifies the qubit state as a direction on the unit sphere, so called the Bloch sphere. The north pole corresponds to $\ket{0}$ and the south pole to $\ket{1}$. Orthogonal vectors are opposite points in the bloch sphere: $(\theta \rightarrow \pi - \theta, \phi \rightarrow -\varphi)$.

Bloch sphere: Hilbert space of one qubit.

The density matrix of one qubit is $\rho = \ket{\psi} \bra{\psi}$, or using the bloch parametrization:

\begin{align*} \rho &= \begin{pmatrix} \cos \theta/2 \\ \E^{\I \varphi} \sin \theta/2 \end{pmatrix} \begin{pmatrix} \cos \theta/2 & \E^{-\I \varphi} \sin \theta/2 \end{pmatrix} \\ &= \frac{1}{2} \begin{pmatrix} 1 + \cos \theta & \E^{-\I \varphi} \sin\theta \\ \E^{\I \varphi} \sin \theta & 1 - \cos \theta \end{pmatrix} \end{align*}

or equivalently

$$\rho = \frac{1+\bm n \cdot \bm \sigma}{2}, \quad \bm n = (\sin\theta \cos \varphi, \sin \theta \sin \varphi, \cos\theta)\,,$$

where $\bm \sigma = (X, Y, Z)$ is the vector of pauli matrices. This form allows a compact representation of a general mixed state of qubits:

$$\rho = \frac{1 + r \bm n \cdot \bm \sigma}{2}, \quad r \le 1\,,$$

where $r=1$ is the pure state and $r<1$ a mixed state, which lies then inside the unit bloch sphere.

The hilbert space of a system of $N$ qubits, is the tensor or Kronecker product of one-qubit spaces:

$$\mathcal{H} = \bigotimes_{n=1}^N \mathcal{H}_n$$

and

$$\ket{s_1}\otimes \ket{s_2} \otimes \ldots \times \otimes \ket{s_N} = \ket{s_1 s_2 \ldots s_N}, \quad s_n=0,1\,,$$

is an element of the canonical basis; sometimes it is convenient to write simply $\ket{s}$, where $s$ is the decimal representation of the binary string $s_1\ldots s_N$:

$$\ket{\psi} = \sum_{s=0}^{2^N - 1} \psi_s \ket{s}\,,$$

is a general expression of a ket, where

$$\sum_s |\psi_s|^2 = 1 \,.$$

Important two qubit states are the Bell states:

\begin{align*} \ket{\Phi_\pm} &= \frac{\ket{00} \pm \ket{11}}{\sqrt{2}} \\ \ket{\Psi_\pm} &= \frac{\ket{01} \pm \ket{10}}{\sqrt{2}} \,. \end{align*}

von Neumann entropy and entanglement

One of the deepest facts about the quantum state was discovered by von Neumann in his investigation of the measurement process: one can associate to a quantum state $\rho$ an entropy:

$$S(\rho) = - \Tr \rho \log \rho\,.$$

This equation defines a fundamental relationship between quantum states and information.

Partial trace

Consider a bipartite system $AB$ whose hilbert space is $\mathcal{H} = \mathcal{H}_A \otimes \mathcal{H}_B$, the $B$ partial trace $\Tr_B$ is a linear operation mapping $\mathcal{H}$ to $\mathcal{H}_A$, such that the expected value of an arbitrary operator $O_A$ satisfies:

$$\braket{O_A} = \Tr O_A \rho_A = \Tr (O_A \otimes 1_B) \rho \,, \rho_A = \Tr_B \rho\,,$$

where $\rho$ is $AB$ state and $\rho_A$ is the state of the subsystem $A$ (note that the first trace is over $A$ space, and the second is on the whole space).

For instance the partial trace over a fourth order tensor $T_{km,ln}$ where the indices $k,l=1, \ldots, L$ refer to space $A$ and the indices $m,n = 1, \ldots, N$ to space $B$, corresponds to the contractions over $B$ indices, $\Tr_B T = T_A$ with $T_A(k,l) = T_{kn,ln}$ (using the einstein convention), or over the $A$ indices $\Tr_A T = T_B$ with $T_B(n,m) = T_{kn,km}$.

Let us apply the partial trace to the Bell state $\ket{\Psi_-}$, which is a state of two qubits $A$ and $B$:

\begin{align*} \rho_A & = \Tr_B \ket{\Psi_-}\bra{\Psi_-} = \frac{1}{2} \Tr_B \left( \ket{01}\bra{01} - \ket{01}\bra{10} - \ket{10}\bra{01} + \ket{10}\bra{10} \right) \\ & = \frac{1}{2} \left( \ket{0}\bra{0}\braket{1|1} + \ket{1}\bra{1}\braket{0|0} \right) \\ & = \frac{1}{2} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \end{align*}

terms with $\braket{0|1}$ vanish; therefore the reduced density matrix is proportional to the identity. $\rho_A$ corresponds then to a mixed state of equally probable $\ket{0}$ and $\ket{1}$ states. We conclude that in general the state of a subsystem of a pure state system is mixed.

We can compute the von Neumann entropy of the whole system and the one of its subsystems:

$$S(AB) = -\Tr \rho \log \rho = -\Tr \ket{\psi} \braket{\psi|\psi} \log(1) \bra{\psi} = 0$$

and

$$S(A) = -\Tr \rho_A \log \rho_A = \frac{1}{2} \log 2 + \frac{1}{2} \log 2 = \log 2 = 1\,.$$

The entropy of the pure state is $0$, while the entropy of its subsystems is $S(A) = S(B) = 1$, the maximum possible value of a two-dimensional system. If we apply a classical reasoning to understand this result we arrive at a contradiction. The entropy of a given system is zero, meaning that it is perfectly ordered, or analogously that we have a perfect knowledge of its state (the equivalence of the two statements derives from the equivalence of the entropy and information), however, the entropy of its subsystems is maximal, meaning that its subsystems are perfectly disordered. This contradiction was first put forward by Schrödinger in his famous response to Einstein, Podolsky and Rose:

the best possible knowledge of a whole does not necessarily include the best possible knowledge of all its parts, even though they may be entirely separated and therefore virtually capable of being “best possibly known” ²

Therefore the Bell state contains correlations that cannot be accounted by classical laws (in this respect we discuss later the Bell theorem), this purely quantum information resource is the entanglement inherent of interacting multiparticle quantum states, a concept first introduced by Schrödinger in the previous paper.

We observe that the von Neumann entropy can be used to measure the entanglement of quantum states. We will illustrate the entanglement as an information resource using a few simple quantum circuits. Before that we introduce the basic elements of a quantum circuits, the quantum gates.

It is also worth mentioning that the reduced density matrix of a pure state corresponds to a mixed state. This is a general fact, one can always enlarge the hilbert space of a composite system in a mixed state $\bar{\rho}$, in such a way that

$$\bar{\rho} = \Tr_A \rho\,,\quad \rho = \ket{\psi} \bra{\psi} \in \bar{\mathcal{H}} \otimes \mathcal{H}_A \,,$$

where the trace is over the ancillary space $\mathcal{H}_A$.

Entangled states

The hilbert space of a general quantum system $\mathcal{H}$ has the structure of a product of hilbert spaces corresponding to its subsystems

$$\mathcal{H} = \mathcal{H}_1 \otimes \mathcal{H}_2 \otimes \ldots$$

For instance, $\mathcal{H}$ represents a set of qubits, of atoms in a condensate, or of spins in a lattice, for which each $\mathcal{H}_n$ stands for a qubit, an atom or a spin, respectively. Often the ground state of these systems has a very simple form: it can be factorized in a product of states of its individual components (or subsystems), like the ferromagnetic phase in which all spins are up:

$$\ket{G} = \ket{0} \otimes \ket{0} \otimes \ldots\,;$$

however, excitations at finite temperature and interactions build much more complex states that cannot be written as a product of basic states belonging to each subsystem. Non-factorizable states are entangled states. The bell states are examples of non-factorizable two qubit states.

Therefore, not entangled pure states of a bipartite system can be expressed as a product,

$$\ket{\psi}^{AB} = \ket{\psi^A} \otimes \ket{\psi^B}\,.$$

The von Neumann entropy of the corresponding parties vanishes, $S(A) = S(B) = 0$.

The density matrix of a two parties system can be decomposed in terms of orthonormal basis vectors, the Schmidt decomposition. It is convenient to write a general pure bipartite state $\ket{\psi}$,

$$\ket{\psi} = \sum_{n^An^B} x_{n^An^B} \ket{a_{n^A}} \otimes \ket{b_{n^B}}$$

using its matrix representation $X$,

$$\ket{\psi} \doteq X$$

where $\mathrm{dim}X= N_A \times N_B$, whose elements are

$$x_{n^An^B} = \braket{a_{n^A} b_{n^B} | \psi}\,,$$

with $\ket{a_{n^A}}$ and $\ket{b_{n^B}}$ the basis vectors of the two parties; we assume $N_A \le N_B$. Consequently, the reduced density matrix of subsystem $A$ is simply the $N_A \times N_A$ matrix,

$$\rho_A \doteq XX^\dagger\,,$$

and similarly for $B$:

$$\rho_B \doteq X^\dagger X\,.$$

Let us diagonalize $\rho_A$,

$$\rho_A \doteq U P U^\dagger, \quad P = \mathrm{diag}(p_{n^A}),\; \mathrm{dim} P = N_A\,,$$

where

$$U = \sum_{n^A} \ket{u_{n^A}} \bra{a_{n^A}}\,, \quad \rho_A \ket{u_{n^A}} = p_{n^A}\ket{u_{n^A}} $$

is the unitary that transforms the $\ket{a}$ basis to the $\ket{u^A}$ basis in which $\rho_A$ is diagonal (note that $\sum_{n^A} p_{n^A} = 1$). We can proceed similarly with the $B$ subsystem, to obtain the reduced matrices in the form:

$$\rho_A = \sum_n p_n \ket{u^A_n}\bra{u^A_n}\,, \quad \rho_B = \sum_n p_n \ket{u^B_n}\bra{u^B_n}$$

where $p_n$ are the nonzero eigenvalues (common to both $A$ and $B$), and $\ket{u_n^B}$ the corresponding $N_A$ eigenvectors of $X^\dagger X$ (whose numbers is $N \le N_A$). In conclusion, we can rewrite the pure state in the form:

$$\ket{\psi} \doteq \sqrt{P}, \quad \ket{\psi} = \sum_n \sqrt{p_n} \ket{u^A_n} \otimes \ket{u^B_n}\,,$$

which is just the schmidt decomposition. Note that the trick to represent the state by a matrix does not work for, for example, a tripartite system; the schmidt decomposition is thus only appropriate for systems divided in two parts.

The schmidt decomposition of a bipartite pure state $\ket{\psi_{AB}}$ gives an explicit expression of the entanglement entropy:

$$S_A = -\sum_n p_n \log p_n$$

where $\sqrt{p_n}$ are the schmidt coefficients in the expansion of $\ket{\psi_{AB}}$. Note that the $S_A$ contains information about the full spectrum of the corresponding density matrix (in the schmidt basis).

Entropy properties

$S(\rho) \ge 0$ and is zero for pure states.
The entropy of a uniformly mixed state of $N$ qubits $\rho = 1_d/d$, where $\mathrm{dim}\mathcal{H}=d= 2^N$ is the number of qubits $N$.
The entropy of the reduced density matrix of a bipartite system $AB$ are equal $S(\rho_A)=S(\rho_B)$.
Let $p_n$ be a probability distribution and $\ket{n} \bra{n}$ orthogonal states of system $A$; suppose $\rho_n$ are states of $B$, then
$$S\left( \sum_n p_n \ket{n} \bra{n} \otimes \rho_n \right) = H(p_n) + \sum_n p_n S(\rho_n)\,,$$
where $H$ is the Shannon entropy.
The entropy is subadditive
$$S(AB) \le S(A) + S(B)$$
The entropy is concave
$$\sum_n p_n S(\rho_n) \le S\left(\sum_n p_n \rho_n \right)\,.$$

To prove the joint entropy formula we solve the eigenvalue equation $\rho_n \ket{u_n^k} = \lambda_n^k \ket{u_n^k}$, which leads to,

$$S\left( \sum_n p_n \rho_n \right) = - \sum_{nk} p_n \lambda_n^k \log p_n \lambda_n^k$$

from which we obtain

$$S\left( \sum_n p_n \rho_n \right) = H(p_n) + \sum_{n} p_n S(\rho_n)$$

The subadditivity of the entropy can be proved using the Klein inequality:

$$\Tr(\rho \log \rho) - \Tr(\rho \log \sigma) \ge 0$$

for arbitrary density matrices $\rho$ and $\sigma$.

Using the joint probability formula and its subadditivity one can demonstrate the concavity property.

Entanglement nonlocality

Some very basic properties of quantum states conflict classical physics. Einstein, Podolsky and Rosen noted that

In quantum mechanics in the case of two physical quantities the knowledge of one precludes the knowledge of the other.⁴

We verified this statement using the bell state and showing that specifying the reduced state of one qubit (say a physical spin for concreteness) destroys the information on the other one. Thus, in apparent contradiction with the fact that the whole system is in a pure state, and then perfectly known. “Apparent” because the physical reality is quantum, not classical, as results form experiments on bell inequalities.⁵

In fact, suppose as before that the two spin system is the $\ket{\Psi_-}$ state; a measurement of $Z_A\otimes 1_2$ projects $\ket{\Psi_-}$ to either $\ket{01}$ or $\ket{10}$, and the result is $1$ or $-1$ with probability $1/2$; therefore, if one measures the second spin $1_2 \otimes Z_B$ the results are similar. However, if the $A$ spin is found to be in the up state $1$, the measure of the second spin $B$ gives $-1$. (Note that these results do not depend on the order of the measurement.) Leading thus to a perfect anti-correlation of both measurements. The question posed by Einstein, Podolsky and Rosen is whether this correlation arises from some hidden reality.

Bell devised a test to verify if the supposed “uncertainty” of quantum mechanics is only due to the existence of a classical underlying physical mechanism, described by a set of hidden variables. We follow here the version of the Bell theorem proposed by Clauser et al.⁶

We consider two agents Alice $A$ and Bob $B$. We discuss first the classical approach. Assume a source ot two-particle states. Alice measures the $A_1$ and $A_2$, two physical quantities related to the first particle and taking the values $a_1,a_2=-1,1$; Bob measures the second particle properties $B_1$ and $B_2$ taking the values $b_1,b_2=-1,1$. We also assume, and this is the connexion with the hidden variables, the source produces its output following some rule to which one can associate certain probability distribution $P(a_1,a_2; b_1,b_2)$. (Remark that a deterministic rule is a special case of probability one.) Therefore, two particle correlations are given by the expectations $\braket{a_i b_j}$ with $i,j=1,2$ (over the probability $P$). Therefore, the quantity $S$ EX

$$S = \braket{a_1b_1} + \braket{a_1b_2} + \braket{a_2b_1} - \braket{a_2b_2}$$

satisfies the classical inequality

$$S \le 2\,.$$

We discuss now the quantum approach. The analog quantum setup is a two spin system whose observables are,

$$A_1 = X_A,\; A_2 = Y_A$$

and

$$B_1 = X_B,\; B_2 = Y_B\,,$$

and the quantum state produced by the source is

$$\ket{\psi} = \frac{1}{\sqrt{2}} \ket{00} + \frac{\E^{\I \pi/4}}{\sqrt{2}} \ket{11}.$$

A simple exercise show that the quantum correlation EX:

$$S = 2 \sqrt{2} > 2$$

in contradiction with the classical expectation. The experimental result refutes the hidden variable hypothesis. In addition, quantum correlations are stronger than classical ones, and their nature is nonlocal: independent measurements of spatially separated qubits can be perfectly correlated. The origin of purely quantum correlations, with no classical equivalent, is the entanglement of composite quantum states.

As an aside remark, let us note that the impossibility to account for quantum properties in terms of classical physics is often the source of the misleading statements, sometimes presented as “quantum paradoxes”: they are much “classical paradoxes” than quantum ones. What we must retain here is that entanglement is a quantum resource of information, with the potential to overcome classical constraints or limitations.

Exercises

Prove the entropy properties.
Show that the measurement of the two qubits of a bell state on an arbitrary direction $\bm n$, leads to perfectly correlated results.

Useful formulas

Convex function $f(x)$.

Gibbs inequality:
$$-\sum_n p_n \log p_n \le -\sum_n p_n \log q_n$$
where $p$ and $q$ are two probability distributions.
Jensen inequality:
$$f(\braket{x}) \le \braket{f(x)}$$
if $f$ is convex; in general, for positive $p_n$ and $f$ convexity implies,
$$f\left(\sum_n p_n x_n \right) \le \sum_n p_n f(x_n)$$
Remember that a function $f$ is convex if for $l\in [0,1]$,
$$f\left(\lambda x_1 + (1-\lambda)x\right) \le \lambda f(x_1) + (1 - \lambda) f(x_2)$$
(then $-f$ is concave, see figure above).
Klein inequality:
$$\Tr \rho \log \frac{\rho}{\chi} \ge 0$$
where $\rho$ and $\chi$ are two arbitrary density matrices; the quantity on the left is the relative entropy. Indeed, using well suited orthonormal basis,
$$\rho = \sum_k p_k \ket{p_k}\bra{p_k},\quad \chi = \sum_l q_l \ket{q_l}\bra{q_l},$$
we write,
$$-\Tr \rho \log \chi = - \sum_{kl} p_k |\braket{q_l|p_k}|^2 \log q_l$$
or equivalently, noting that $X_{lk} = |\braket{q_l|p_k}|^2$ is a double stochastic matrix (their marginal sums are probability distributions),
$$-\Tr \rho \log \chi = -\sum_k p_k \left( \sum_l X_{lk} \log q_l \right)$$
from which, using the jenssen inequality, we obtain,
$$-\Tr \rho \log \chi \ge -\sum_k p_k \sum_l \log \left( \sum_l X_{lk} q_l \right)$$
We apply now the gibbs inequality to the last term (we can put $\sigma_k = \sum_l X_{lk} q_l$, with $\sum_k \sigma_k = 1$),
$$-\sum_k p_k \sum_l \log \left( \sum_l X_{lk} q_l \right) \ge -\sum_k p_k \log p_k$$
to arrive at
$$-\Tr \rho \log \chi \ge - \Tr \rho \log \rho\,.$$

Notes

B. Schumacher, Quantum coding, Phys. Rev. A 51, 2738 (1995). .pdf ↩
E. Schrödinger, Discussion of probability relations between separated systems, Mathematical Proceedings of the Cambridge Philosophical Society 31, 555 (1935) .pdf ↩
A. Barenco et al., Elementary gates for quantum computation, Phys. Rev. A 52, 3457 (1995). Universality of the set one qubit and controlled not gates. ↩
A. Einstein, B. Podolsky, and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47, 777 (1935) ↩
A. Aspect, Closing the door of Einstein and Bohr quantum debate, Physics (APS) 8, 123 (2015) .pdf ↩
J. Clauser, M. Horne, A. Shimony, and R. Holt, Proposed Experiment to Test Local Hidden-Variable Theories, Phys. Rev. Lett. 23, 880 (1969) ↩