\(\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle}\) \(\newcommand{\bm}{\boldsymbol}\)
Topics
- Quantum principles, density matrix and entanglement
- Random quantum states and Don Page entropy formula
- Gates and simple circuits, superdense coding, teleportation, Deutsch algorithm, Grove search algorithm
- Quantum walks
- Quantum chaos: the kicked rotator and dynamical localization
Problems
1
Density matrix. A quantum system consists in two parts A and B. Show that the expected value of an operator \(O\) acting on A,
where \(I_B\) is the identity in the B hilbert spaca \(\mathcal{H}_B\), is given by the partial trace, over B, of the AB density matrix \(\rho\),
As an application take a two spins state:
and compute the expected value of \(X\) and \(Z\) (the A pauli matrix in the \(x\) and \(z\) directions). Compare with the single spin state \((\ket{0} + \ket{1})/\sqrt{2}\).
2
Bell state entanglement. Consider a bipartite system AB, and the dichotomic variables \(a,c=\pm1\) of A and \(b,d=\pm1\) of B. Show that,
Demonstrate that the expected value \(\braket{x}\) satisfies \(\braket{x} \le 2\).
Now consider a quantum equivalent system:
Demonstrate that,
in contradiction to the classical result. Compute the expected value of \(X\) in the state,
where the measure axes are in the plane \(xz\) with angles with respect to the \(z\) axis \(\theta_a = 0\), \(\theta_b = \pi/2\), \(\theta_c = \pi/4\), and \(\theta_d = -\pi/4\).
3
The Greenbergm Horne and Zeilinger paradox. Consider the state GHZ of a three parts system ABC:
Show that the operators in the set \(\mathcal{S}\), have eigenvalue 1:
where, for instance, \(YXY = Y_A \otimes X_B \otimes Y_C\) and \(ZZ1 = Z_A \otimes Z_B \otimes I_C\).
Consider now a classical equivalent system for which the value of the observables in \(\mathcal{S}\) can take the values \(m(\mathcal{S}) = \pm 1\). Show then that,
leads to a contradiction \(-1=1\).
4
Teleportation. Alice and Bob share the bell state,
In addition, Alice possesses an arbitrary state \(\ket{\psi} = a \ket{0} + b \ket{1}\). Show that the three qubit state can be written as,
a decomposition in the bell states:
Explain how the information in possession of Alice (the bell states) may lead Bob to recover the initially Alice \(\ket{\psi}\) state.
Answer: \(\ket{\Phi_+} \rightarrow Z\), \(\ket{\Phi_-} \rightarrow I\), \(\ket{\Psi_+} \rightarrow ZX\), and \(\ket{\Psi_-} \rightarrow X\).
5
The Deutsch-Jozsa algorithm. We want to determine if certain boolean function \(f\) of \(n\) bits,
is “constant” or “balanced”. In the first case, the constant value of \(f\) can be either 0 or 1, whatever the set of input bits. In the second case, \(f=0\) for exactly half of the possible input values of \(\{x_1,\ldots,x_n\}\), and \(f=1\) for the other half.
- How many evaluations of \(f\) are necessary to decide classically if it is constant or balanced?
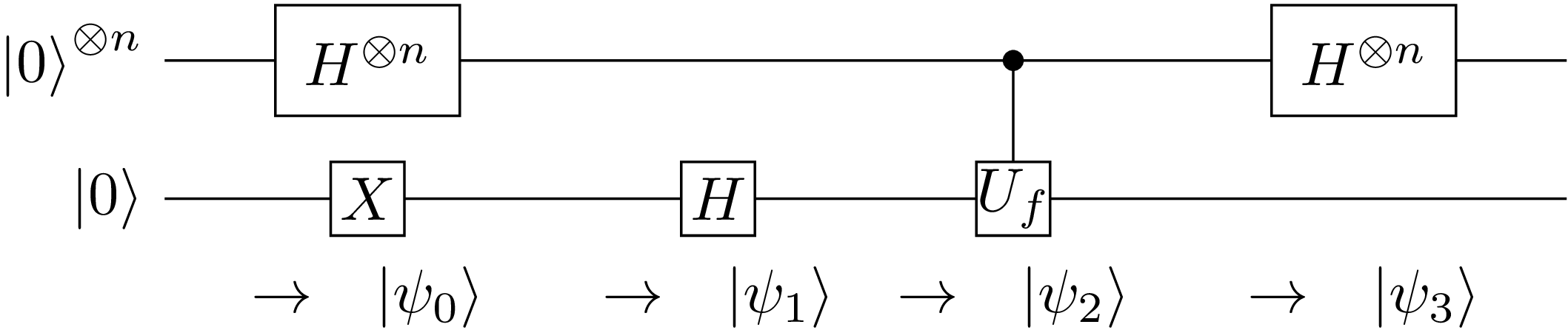
Deutsch devised a quantum algorithm which only needs one evaluation of \(f\), using the circuit:
where the unitary operator \(U_f\) is defined by
with the notation \(\ket{x}\) for the state of the first \(n\) qubits (top wire of the circuit), and \(\ket{b}\) for the last qubit (bottom wire). Initially the \(n+1\) qubits are in the state \(\ket{0}\)
-
Compute the state \(\ket{\psi_0}\) after the application of the operator \(X\) to the last qubit.
-
Compute the state \(\ket{\psi_1}\) after the application of the Hadamard operator to all qubits.
-
Show that the state of the last qubit remains the same, up to a phase factor,
$$ \ket{-} = \frac{\ket{0}-\ket{1}}{\sqrt{2}} $$after the \(U_f\) step. The phase factor depends on the value of \(f\).
Determine the state \(\ket{\psi_2}\) after applying \(U_f\).
-
Demonstrate that after the last application of the Hadamard operator to the first \(n\) qubits, the final state is,
$$\ket{\psi_3} = \frac{1}{2^{n}} \sum_{x,y\in\{0,1\}^n} (-1)^{\langle x,y \rangle + f(x)} \ket{y} \otimes \ket{-} $$Hint. As an intermediate computation you may demonstrate that,
$$H^{\otimes n} \ket{0} = \frac{1}{\sqrt{2^n}} \sum_{x\in\{0,1\}^n} \ket{x}$$(which gives you \(\ket{\psi_1}\)), and
$$H^{\otimes n} \ket{x} = \frac{1}{\sqrt{2^n}} \sum_{y\in\{0,1\}^n} (-1)^{\langle x,y \rangle} \ket{y}$$which will give you the \(\ket{\psi_3}\) state.
-
Explain how one may distinguish between the two cases, constant or balanced, using the properties of the final quantum state. Can we answer the question with certainty?
6
Quantum walk. Investigate the pseudo-energy spectrum of a one dimensional quantum walk defined by the step operator \(U = SC\) with coin,
and motion,
Find the expression of the effective hamiltonian in the limit \(k \rightarrow 0\) and compare the result with the Dirac hamiltonian.