Irreversibility | Random physics

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Di}[1]{\mathop{}\!\mathrm{d}#1\,} \newcommand{\Dd}[1]{\frac{\mathop{}\!\mathrm{d}}{\mathop{}\!\mathrm{d}#1}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle}$

Lectures on statistical mechanics.

Equilibrium and irreversibility

An ensemble of classical mechanical systems formed by a large number of particles $N$ can be described by a distribution function $\rho$ in phase space $\Gamma = \mathcal{X} \mathcal{P} \subset \mathbb{R}^{3N} \times \mathbb{R}^{3N}$,

$$\rho = \rho(x,p,t), \; x = (\boldsymbol x_1,\ldots, \boldsymbol x_N) \in \mathcal{X}, \; p = (\boldsymbol p_1,\ldots, \boldsymbol p_N) \in \mathcal{P},$$

such that

$$\frac{1}{N!}\int_\Gamma \D x \D p \, \rho(x,p,t) = 1\,.$$

where the prefactor accounts for the particle permutations. The quantity $\rho d\Gamma$ is a measure of the probability of the ensemble to be in the “cell” $d\Gamma = \D x \D p$ of the phase space (a microscopic state of the mechanical system).

The Liouville theorem ensures the conservation of $\rho$:

$$ \begin{equation} \label{liouville} \frac{\D \rho}{\D t} = \frac{\partial \rho}{\partial t} + \{\rho, H\} = 0 \end{equation} $$

where the system’s hamiltonian $H$ is independent of time; here,

$$\{f,g\} = \frac{\partial f}{\partial x} \frac{\partial g}{\partial p} - \frac{\partial f}{\partial p} \frac{\partial g}{\partial x}$$

is the Poisson bracket. The density $\rho$ contains all the information about the system and the associated Gibbs entropy

$$S_G = - \int_\Gamma \D \Gamma \rho(\Gamma) \ln \rho(\Gamma)$$

is constant in time (it is the thermodynamic entropy only in the case of an equilibrium ensemble).

From the global quantity $\rho$, global in the sense that it depends on all configurations of all particles, one can define local properties as for example quantities associated with one particle:

$$f(\boldsymbol x, \boldsymbol p, t) = \frac{N}{N!} \int_{\Gamma_{\bar{1}}} \prod_{n=2}^N \D \boldsymbol x_n \D \boldsymbol p_n \, \rho(x, p, t)$$

where $\boldsymbol x = \boldsymbol x_1$ and $\boldsymbol p = \boldsymbol p_1$, and $\bar{1}$ denotes the set of all particles but one; $f_1 = f$ is the one particle distribution function, with normalization,

$$\int_{\Gamma_1} \D \Gamma_1 f(\Gamma_1, t) = N\,, \quad \D \Gamma_1 = \D \boldsymbol x \D \boldsymbol p,$$

where we introduced the notation $\Gamma_n = (\boldsymbol x_n, \boldsymbol p_n)$. In the same way we may define the $n$-particles distribution function”

$$f(\boldsymbol x_1, \boldsymbol p_1, \ldots, \boldsymbol x_n, \boldsymbol p_n, t) = \frac{1}{(N-n)!} \int_{\Gamma_{\bar{1}}} \prod_{k=n+1}^N \D \boldsymbol x_k \D \boldsymbol p_k \, \rho(x, p, t)\,.$$

At variance to the Gibbs entropy, the Boltzmann entropy

$$ \begin{equation} \label{sb} S_B = - \int_{\Gamma_1} \D \boldsymbol x \D \boldsymbol p \, f(\boldsymbol x, \boldsymbol p,t) \ln f(\boldsymbol x, \boldsymbol p,t), \end{equation} $$

evolves in time. For instance if the hamiltonian $H=H_1 + H_2$ contains, in addition to the one particle term $H_1$, a two particle interaction $H_2$ depending on the distance between these two particles, it is easy to demonstrate that integrating the Liouville equation ($\ref{liouville}$) over $\Gamma_{\bar{1}}$, one obtains an equation of the form (Boltzmann equation):

$$ \begin{equation} \label{boltzmann} \frac{\partial f}{\partial t} + \{f, H_1\} = C[f(\Gamma_2)] \end{equation} $$

where $f_2 = f(\Gamma_2)=f(\boldsymbol x_1, \boldsymbol p_1. \boldsymbol x_2, \boldsymbol p_2,t)$ is the two particle distribution function (BBGKY hierarchy), and $C$ is the collision term accounting for the interactions between the two particles. In particular, for a diluted gas Boltzmann assumed that

$$f_2 \sim f_1 f_1,$$

thus neglecting correlations between the two particles (Stosszahlansatz, or molecular chaos hypothesis), which leads to his famous H-theorem, stating that $S_B$ can only increase in time:

$$\frac{\D S_B}{\D t} \ge 0\,.$$

The neglect of correlations translates into a loss of information about the system’s state and hence in an increase of its entropy. However, relaxation towards an equilibrium state (not necessarily a thermal one) with concomitant increase of the entropy, the properties of an irreversible evolution, are possible without any disorder or probabilistic hypothesis. Indeed, equilibration of local observables can arise in the dynamics of reversible systems (invariant under time reversal) as a consequence of the limit of a large number of particles. It is worth noting that such kind of relaxation process applies to local quantities like the one particle density

$$n(\boldsymbol x, t) = \int \D \boldsymbol p \, f(\boldsymbol x, \boldsymbol p, t)$$

global ones like $\rho(\Gamma, t)$ do not show relaxation, of course:

Local observables of a global reversible system initially in a low entropy state, can relax to equilibrium values in the limit of a large number of degrees of freedom ($N \rightarrow \infty$).

We show in two specific examples that this statement applies to classical as well quantum systems. Our first example is the expansion of an ideal gas (Swendsen, 2008). For a historical perspective and a conceptual discussion about the problem of irreversibility, read the paper by Lebowitz (1993).

Expansion of an ideal gas

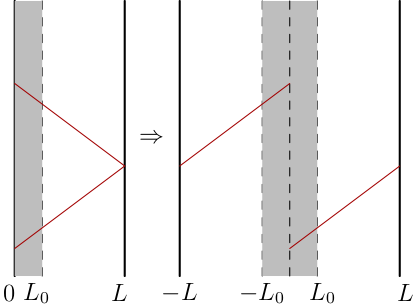
We consider a gas initially confined in a region of width $L_0$ of a box of size $L$ (in one dimension, and homogeneous in the other dimensions, see the figure below). At $t=0$ the gas is allowed to expand freely; wall collisions are assume perfectly elastic. The system conserves the total energy and the momentum of each of the $N$ particles. The absence of interactions allows a factorisation of the density function in a product of one particle distributions $\rho \sim \prod f_1$. The initial condition can be chosen in the form of a separated momentum and position variables $f_1(x,p,0) \sim g(p) n_0(x)$ ($x$ and $p$ are here the one particle canonical variables), because, due to momentum conservation, $g(p)$ remains unchanged for $t>0$. The question is whether the time evolution of the density $n$ tends to a stationary state. We take,

$$n_0(x) = \frac{N}{L_0} [\theta(x) - \theta(x - L_0]\,,$$

and

$$g(p) = \frac{1}{\sqrt{2\pi T}} \E^{-p^2/2T}\,,$$

a maxwellian distribution.

Doubling the size of the box to represent collisions by periodic boundary conditions: the discontinuity translates in fourier amplitudes decreasing like $\sim 1/k$ for mode $k$.

The time evolution of $f_1$ is governed by the Boltzmann equation ($\ref{boltzmann}$) with vanishing collision term. Using the characteristics we find,

$$n(x,t) = \int_{-\infty}^\infty \D p \, g(p)n_0(x-pt), \quad 0\le x \le L\,,$$

(we put the mass of the particles $m=1$). Doubling the size of the box ($-L \le x \le L$) the discontinuous function (due to the collisions) $n(x,t) = n_0(x-pt)$, becomes periodic and can be expanded in fourier series:

$$n_0(x) = \sum_{k \in \mathbb{Z}} n_k \E^{\I \pi k x/L}\,, \quad n_k = \frac{N}{L_0}\int_{-L_0}^{L_0} \frac{\D x}{2L} \E^{\I \pi k x/L} = \frac{N}{L} \delta_{k,0} + \frac{N}{\pi k L_0} \sin\left(\frac{\pi k L_0}{L}\right)\,.$$

Inserting this expression into $n(x,t)$ leads to a gaussian integral over $p$; integration gives an exact formula for the time evolution of the density:

$$n(x,t) = \frac{N}{L} + \frac{2N}{\pi L_0} \sum_{k=1}^\infty \frac{1}{k} \sin\left(\frac{\pi k L_0}{L}\right) \cos\left(\frac{\pi kx}{L}\right)\E^{-\pi^2 T k^2 t^2/2L^2}$$

The sum in this formula is rapidly convergent, and shows that for large times,

$$ n(x,t) \rightarrow \frac{N}{L},\; \mbox{for}\; t \gg \tau = \sqrt{T/L^2}$$

corresponding to the equilibrium value of the density: after expansion the gas occupies uniformly the available volume. Note that the type of relaxation we found do not (formally) breaks the $t \rightarrow -t$ symmetry; however, irreversibility here is related with the initial condition, having lower entropy than the final state (due to the isothermal expansion of the ideal gas). It is also important to keep in mind that the total one particle distribution function $f_1(x,p,t) = g(p) n_0(x-pt)$ is a quasi-periodic function: relaxation appears as an infinite superposition of oscillating exponentials,

$$\int dp \E^{\I p t - p^2/2T} \sim \E^{-T t^2/2}\,.$$

A related phenomenon is given by the Landau damping of the electrostatic energy in a collisionless plasma; in this case relaxation towards equilibrium is exponential in time.

Spin chain

Our second example is a one-dimensional chain of quantum spins, with hamiltonian:

$$H = -B\sum_{n=1}^N \sigma_n + \sum_{n=1}^N \sum_{m=1}^{N/2} J(m) \sigma_n \sigma_{n+m}$$

and periodic boundary conditions ($n+m$ is modulo $N$); here $\sigma=\sigma_z$, moreover we define the rise and lower spin matrices $\sigma^\pm = (\sigma_x \pm \I \sigma_y)/2$, where $\boldsymbol \sigma$ are the usual Pauli matrices. The constant $B$ represents the applied magnetic field, and $J(m)$ is the interaction between spins (in convenient units). Later we will assume that $J(m) \sim 2^{-m}$. This model was proposed by Emch to explain an experiment on free-induction relaxation of nuclear spins attached to a crystal lattice and interacting by long range forces. Here, we follow the presentation by Thirring¹.

We are interested in the time evolution of a local observable, starting form a low entropy initial state. As the local observable we take the $z$ component of the $n$ spin $\sigma_n$, and the initial state:

$$\rho(0) = \prod_{n=1}^N \rho_n(0),\quad \rho_n(0) = \frac{1}{2}(1 + \boldsymbol s_n \cdot \sigma),$$

with

$$\boldsymbol s_n = (\sqrt{1-s^2} \cos\alpha_n, \sqrt{1-s^2}\sin\alpha_n,s)$$

where $0\le s \le1$ and $\alpha_n$ are arbitrary phases. $\rho(0)$ is a pure (product) state which gives the expected value:

$$\braket{\sigma_n(0)} = s\,,\quad \braket{\sigma^\pm_n(0)} = \frac{1}{2}\sqrt{1-s^2} \E^{\pm \I \alpha_n}$$

of the initial spin (or equivalently $\braket{\boldsymbol \sigma_n} = \boldsymbol s_n$); spins at different sites are then initially uncorrelated. However, under time evolution

$$\boldsymbol \sigma(t) = \E^{\I H t} \boldsymbol \sigma \E^{-\I H t}$$

the interaction creates correlations between distant spins. A lengthy but straightforward calculation, using the relation $f(\sigma)\sigma^+ = \sigma^+ f(\sigma + 2)$, leads to the exact formula EX,²

$$\braket{\sigma^+_n(t)} = \frac{\sqrt{1-s^2}}{2} \E^{\I \alpha_n + \I 2B t} f_N^2(t)$$

with

$$f_N(t) = \prod_{n=1}^{N/2} \left[ \cos 2J(n)t + \I s \sin 2J(n)t \right]$$

To obtain explicit expressions it is convenient to take $s=0$ (the spin precesses in the $xy$ plane) and $J(n)=2^{-n-1}$:

$$f_N(t)= \prod_{n=1}^{N/2} \cos 2^{-n}t \rightarrow f(t) = \frac{\sin t}{t}$$

in the limit $N\rightarrow\infty$. The last formula can be easily demonstrated using recurrently the elementary trigonometric formula $\sin t = 2 \sin(t/2) \cos(t/2)$. In particular for finite $N$ we have:

$$f_N(t) = \frac{\sin t}{t} \frac{2^{-N/2}t}{\sin 2^{-N/2}t}.$$

It is worth noting that for fixed $N$, the limit,

$$\lim_{t\rightarrow\infty} f_N(t)\,, $$

does not exist; however, inverting the limits order, we get, for fixed time,

$$\lim_{N\rightarrow\infty} f_N(t) = \frac{\sin t}{t} \rightarrow 0 \quad (t \rightarrow\infty)\,.$$

Whence, taking first the “thermodynamic” limit and then the time to infinity, gives us a well defined behavior: a spin relaxation to an equilibrium value.

Indeed, the mean spin at site $n$ is, in the large number of particles limit, writes in the general case,

$$\braket{\boldsymbol \sigma_n(t)} = \left( \sqrt{1-s^2} \cos(\alpha_n +2Bt) f^2(t), \sqrt{1-s^2} \sin(\alpha_n +2Bt)f^2(t) ,s \right)\,.$$

So, in the case $s=0$, we find in the large time limit,

$$\braket{\boldsymbol \sigma} \rightarrow (0,0,0)\,,$$

a relaxation to zero spin, which is an irreversible behavior. For $s \ne 0$ the fact that $f$ tends to zero for large times remains true.

Therefore, we demonstrated that in the “thermodynamic” limit $N\rightarrow\infty$, the inital state relaxes to an equilibrium state $f(t)\rightarrow 0$ (for $t\rightarrow\infty$), with mean zero spin $\braket{\boldsymbol \sigma_n} = 0$ (or $s$ for the conserved $z$ spin component), and the approach to equilibrium is oscillatory (as in the experiment). The expression of $f_N$ shows that the recurrence time is exponentially long $\sim 2^{N/2}/\pi$. A remarkable point is that the order in which the two limits are taken is relevant, reversing the order do not lead to the same result: for finite $N$ the long time behavior is always quasiperiodic, without relaxation.

Using the equilibrium value of the spin:

$$\braket{\boldsymbol \sigma_n} = \mathrm{Tr}\, \rho_n \sigma_n = (0,0,s)$$

we find the final state:

$$\rho_n = \frac{\E^{-\beta \sigma_n}}{\mathrm{Tr}\, \E^{-\beta \sigma_n}}$$

corresponding to the canonical ensemble with “temperature” $\tanh \beta = s$. This result is also remarkable: in the $N\rightarrow\infty$ limit, a spin in a particular site of the lattice, behaves as a (open) subsystem in a larger system: the canonical distribution is the appropriated one for such a situation.

Finally, the approach to equilibrium usually implies a variation of the entropy:

$$S_n(t) = - \mathrm{Tr} \, \rho_n(t) \ln \rho_n(t)$$

of spin $n$. The time evolution of the initial state $\rho_n(0)$ is also determined by the function $f$:

$$\rho_n(t) = \frac{1}{2} [1 + \boldsymbol s_n(t) \cdot \sigma]$$

with $\boldsymbol s_n(t)$ such that $\braket{\boldsymbol \sigma_n(t)} = \mathrm{Tr}\, \rho_n(t) \boldsymbol \sigma = \boldsymbol s_n(t)$. The two eigenvalues of $\rho_n$ are

$$p_n^\pm(t) = \frac{1 \pm s_n(t)}{2}, \quad s_n(t) = |\boldsymbol s_n(t)| = \left( s^2 + (1-s^2)f^4(t) \right)^{1/2}$$

from which we deduce the formula for the entropy:

$$S_n(t) = -\sum_{x=+,-} p_n^x(t) \ln p_n^x(t)$$

which increases in an oscillatory way, and not monotonically as in usual thermodynamic relaxation.

Notes and exercices

Thirring, W. Quantum mathematical physics, (Springer, 2002) (.pdf) ↩
We first demonstrate that $f(\sigma) \sigma^+ = \sigma^+ f(\sigma + 2)$. It is enough to compute the commutator:

$$\sigma \sigma^+ = \sigma^+ \sigma + 2$$

and to observe that we can write $f$ as a power series,

$$f(\sigma) = \sum_k f_k \sigma^k = \sum_{k=2n} f_k + \sigma\sum_{k=2n+1} f_k$$

where we used $\sigma^2 = 1$. Applying to the right $\sigma^+$, we get the result.

The heisenberg operator $\sigma_n^+(t)$, can now be computed. Let us isolate the $n$ term of the interaction in the hamiltonian:

$$h_n = \sigma_n \sum_{m=1}^{N/2} J(m) (\sigma_{n+m} + \sigma_{n - m})$$

hence,

$$ \begin{align*}\E^{\I h_n(\sigma_n) t} \sigma^+ \E^{-\I h_n(\sigma_n) t} & = \sigma^+ \E^{\I h_n(\sigma_n + 2) t} \E^{-\I h_n(\sigma_n) t} \\ &= \sigma^+ \prod_{m=1}^{N/2} \exp\left[ \I 2 J(m) (\sigma_{n+m} + \sigma_{n - m}) \right]\end{align*} $$

where we used that the exponential operators commute. The pauli matrices satisfy the identity,

$$\E^{\I \theta \boldsymbol{n}\cdot \sigma} = \cos(\theta) + \I \sin(\theta) \, \boldsymbol n \cdot \boldsymbol \sigma$$

where $\boldsymbol n$ is a unit vector and $\theta$ is an angle (polar angle in spherical coordinates). Hence,

$$ \begin{align*}\sigma^+_n(t) & = \sigma^+ \E^{\I 2 B t} \\ & \prod_{m=1}^{N/2} \left[ \cos(2J(m)t) + \I \sin(2J(m)t)\, \sigma_{n+m} \right]\\ & \quad \left[ \cos(2J(m)t) + \I \sin(2J(m)t) \, \sigma_{n-m} \right]\end{align*} $$

where we included the external field term of the hamiltonian. Taking the mean value of this last expression gives the formula of the text. ↩