Random physics

Alberto Verga, research notebook

AV I am Alberto Verga, professor at Aix-Marseille University. I work at the Centre de physique théorique on condensed matter and statistical physics. In the last years I investigated transport properties of strong spin-orbit coupling materials in the presence of magnetic disorder. In parallel I conducted a research program on magnetic textures (skyrmions) and their topological transitions, with applications on spin-current controlled transport. More recently, I was interested in quantum information, in particular about the generation of entanglement and its relation with the topological properties of particle-spin interacting systems.

Contact:

Selected publications

For a more complete list see ORCID records or Google Scholar

Some interesting research subjects

Topological insulators

Distinctive properties of topological insulators arise from the intimate coupling of spin and momentum combined with time reversal invariance. When time reversal invariance is broken at the surface but preserved in the bulk, original phenomena emerge as a result of the topological magnetoelectric effect; in particular, the response to applied electromagnetic fields becomes quantized.

Current in a topological insulator
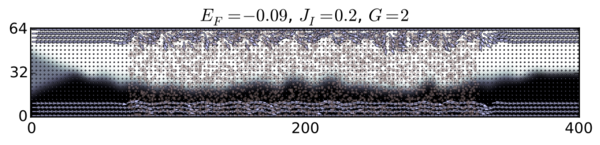
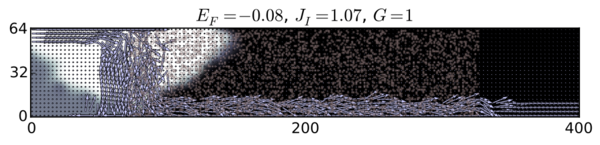
(1) G=2
(2) G=1
The current is carried by edge states: (1) the conductance is quantified G = 2 e2/h;
(2) disorder induces a quantum transition towards a G = 1 e2/h conductance state.

The helicity of the electron states and the magnetic structure are both related with the absence of inversion symmetry, which is just a necessary prerequisite for the observation of the Dzyaloshinskii-Moriya magnetic interaction leading to the helical magnetic states. These helical magnetic states, analogous to the periodic skyrmion states observed in helical magnets, possess a nontrivial topology. Therefore they should modify, through the topological magenetoelectric effect, the transport properties of the surface states, by the excitation of exotic quasiparticles (like dyons).

Within this framework, I am interested in investigating the following open questions:

  • Helical magnetic state: The first problem is to determine under which conditions the magnetic impurities spontaneously organize (as a function of the disorder strength, for instance) into an ordered magnetic phase. An interesting point is whether a helical magnetic state can be established by the Dzyaloshinskii-Moriya effective interaction.

  • Transport: Second, a helical magnetic state is characterized by nontrivial topological charge (skyrmions). As a consequence of the magnetoelectric effect, these magnetic charges will carry an electric charge, forming in principle bound excitations (dyons). Two questions are then in order: what is the nature of these excitations, and how they can influence the transport properties under the action of an external electric field.

Magnetic singularities

The technological applications, notably in spintronics, of electrically controlled magnetic configurations, such as vortices and domain walls driven by spin currents, as well as the richness and novelty of fundamental physical mechanisms, sustain the continued interest in the magnetization dynamics of nanoscale ferromagnets. Applications are often based on processes leading to changes in the topology of the magnetization texture (vortex creation and annihilation, switching of vortex cores, etc.), which imply the formation of singularities. The full description of these singularities, Bloch points in three dimensions, needs to take into account quantum effects (usually at the semiclassical level), beyond the usual micromagnetic approach.

Transition from a skyrmion to a ferromagnetic state driven by a spin polarized current
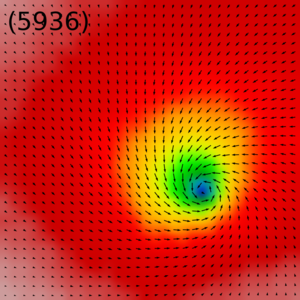
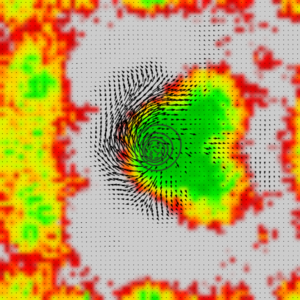
magnetization   phase   spin current
magnetization vector field magnetization phase spin of electrons

In this context, it is worth considering the dynamics of a magnetic skyrmion in a helical metal, connected to leads carrying a spin polarized current. The physics of such a system is rich: even the simplest scattering problem under nonequilibrium conditions involves subtle mechanisms, related to the spin-transfer torque. The traditional approach to this system assumes a homogeneous and stationary current, in order to investigate the skyrmion dynamics. However, the complementary problem, associated to the self-organization of the conduction spins, also deserves attention.

As a natural extension of the previous questions to a three dimensional texture, one particularly interesting subject is the interaction of a Bloch point with a spin polarized current. Remarkably, in recent experimental work, stable Bloch points have been observed in cylindrical magnetic nanowires. This geometry as well as the long live of the singular magnetization distribution, are ideally suitable for a theoretical treatment amenable to be compared with the experiment.

Open systems

Dissipation, relaxation and transport in mesoscopic quantum systems are very active subjects. New phenomena and original concepts arise from disorder and time dependence. Disorder can induce in addition to the usual Anderson transition, a transition from a strong spin-orbit coupled metal to a topological insulator. A periodically driven two dimensional system (semiconductor quantum well, graphene, etc. excited by light or high frequency electric potentials) develops a variety of quantum topological phases with protected edge states. A simple quantum walk with dissipation can have trapped states, also a topological effect. As in classical systems, the existence of a stationary state in a dissipative quantum many-body system driven by static fields, is not guaranteed, and genuine time dependent phenomena may arise.

Mesoscopic systems are ideal candidates to study these nonequilibrium processes. For instance, the effect of a magnetic impurity on the helical modes of a topological insulator driven by a laser pulse. In this system the coupling of plasmons with the helical liquid gives rise to collective spin-plasmon excitations.