Moment Angulaire | Random physics

$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}{\boldsymbol}$

Cours de mécanique quantique.

Algèbre du moment angulaire

Lors de l’étude des symétries dans l’espace de hilbert, nous avons trouvé que le générateur de rotations dans l’espace $\bm L$ obéit aux règles de commutation ($\hbar=1$)

$$ \begin{equation} \label{e:LLL} [L_x,L_y] = \I L_z,\; [L_z,L_x] = \I L_y,\; [L_y,L_z] = \I L_x, \end{equation} $$

ou, d’une façon plus condensée,

$$ [L_i,L_j] = \I \varepsilon_{ijk} L_k\,,\; \bm L \wedge \bm L = \I \bm L, $$

avec $\varepsilon_{ijk}$ le tenseur complètement antisymétrique de Livi-Civita (où on utilise la convention d’Einstein par laquelle on somme sur les indices répétés, ici $k$). On observe que ces relations de commutations sont identiques à celles satisfaites par le spin $\bm S$. En fait, on peut prendre les relations de commutation comme étant la définition des générateurs de rotations, soient-elles intrinsèques comme le spin $\bm S$, ou reliés au mouvement, comme pour le moment orbital $\bm L$, ou même à leur composition $\bm J = \bm L + \bm S$, le moment angulaire total.

On se propose maintenant de déterminer le spectre (valeurs et vecteurs propres) de l’opérateur du moment angulaire en nous basant exclusivement sur les relations de commutation. Le premier obstacle découle des ces relations elles-mêmes, car elles montrent qu’il n’existe pas de base commune aux trois composantes de $\bm L$: ils sont des opérateurs incompatibles. Par contre, on vérifie par un calcul direct que la valeur absolue $L^2$ commute avec une quelconque composante:

$$ \begin{equation} \label{e:LL2z} [L^2,L_z]=0 \,, \end{equation} $$

ce qui implique qu’il existe une base commune aux opérateurs compatibles $L^2$ et $L_z$. Notons par $\ket{lm}$ les vecteurs de la base commune:

$$ \begin{equation} \label{e:Llm} L^2 \ket{lm} = l(l+1) \ket{lm}\,,\quad L_z \ket{lm} = m \ket{lm} \end{equation} $$

où nous avons défini les valeurs propres en fonction de deux paramètres $l$ et $m$, pour le moment arbitraires, qu’on justement veut déterminer.

Il convient d’introduire les opérateurs (non hermitiques) d’échelle:

$$ L_+ = L_x + \I L_y, \quad L_- = L_x - \I L_y,\quad L_+ L_- = L^2 - L_z(L_z - 1), $$

(notez que leur produit est hermitique) lesquels satisfont les règles de commutation:

$$ \begin{equation} \label{e:LLpLmC} [L_+,L_-] = 2 L_z, \quad [L_\pm,L_z] = \mp L_\pm. \end{equation} $$

Il se trouve que $L_\pm$ agissent sur la base commune de $L^2$ et $L_z$ d’une façon analogue aux opérateurs $a$ et $a^\dagger$ de annihilation et création de l’oscillateur harmonique.

On étudie d’abord comment $L_\pm$ agissent sur les états $\ket{lm}$, en utilisant les commutateurs avec $L^2$ et $L_z$:

$$ L^2 L_\pm \ket{lm} = L_\pm L^2 \ket{lm} = l(l+1)L_\pm \ket{lm}\,, $$

puisque $[L^2,L_\pm]=0$,

$$ L_z L_\pm \ket{lm} = (L_\pm L_z \pm L_\pm) \ket{lm} = (m \pm 1) L_\pm \ket{lm} $$

puisque $[L_z,L_\pm] = \pm L_\pm$. On déduit que le ket $L_\pm\ket{lm}$ est un vecteur propre de $L_z$ avec valeurs propres $m \pm 1$. D’une façon équivalente, on a:

$$ \begin{equation} \label{e:Lcpcm} L_+ \ket{lm} = c_+ \ket{l,m+1}\,, \quad L_- \ket{lm} = c_- \ket{l,m-1}\,, \end{equation} $$

dont les constantes $c_\pm$ sont déterminées par la condition de normalisation:

$$ |L_\pm \ket{lm}|^2 = \braket{lm|L_\mp L_\pm| lm} = \braket{lm| L^2 - L_z(L_z \mp 1) |lm} \le 0 $$

ce qui conduit, en supposant $\braket{lm|lm} = 1$, aux deux conditions,

$$ \begin{equation} \label{e:Lcondlm} l(l+1) - m(m - 1) \le 0 , \; l(l+1) - m(m + 1) \le 0 \; \Rightarrow \; -l \le m \le l \,, \end{equation} $$

ainsi qu’aux équations (en unités SI)

$$ \begin{align} \label{e:LLpLm} L_+ \ket{lm} &= \hbar \sqrt{l(l+1) - m(m+1)} \, \ket{l,m+1}\,, \nonumber \\ L_- \ket{lm} &= \hbar \sqrt{l(l+1) - m(m-1)} \, \ket{l,m-1}\,. \end{align} $$

Les opérateurs d’échelle $L_\pm$ permettent de passer de l’état $\ket{lm}$ à l’état $\ket{lm \pm 1}$, d’où en fait leur nom (la valeur de $l$ ne change pas).

La valeur de $m$ est donc bornée par celle de $l \le 0$ ($L^2$ est positif). Or, comme on vient de le voir $L_+$ augmente de une unité la valeur de $m$, tandis que $L_-$ la diminue d’une unité; il doit donc exister des entiers $n_+$ et $n_-$ tels que le vecteur propre $(L_\pm)^{n_\pm} \ket{lm}$ de $L_z$

$$ L_z (L_\pm)^{n_\pm} \ket{lm} = (m \pm n_+) (L_\pm)^{n_\pm} \ket{lm} $$

correspond à une valeur propre $m \pm n_\pm$ de $L_z$ qui éventuellement puisse dépasser les bornes $\pm l$. Il faut par conséquent que la succession s’arrête, et donc qu’il existe des $n_\pm$ pour lesquels

$$ l = m + n_+\,, \quad -l = m - n_- \; \Rightarrow \; 2l = n_+ + n_- \in \mathbb{N} , $$

c’est-à-dire $2l$ doit être entier positif. En conclusion, on a donc démontré que $l$ ne peut prendre, en principe, que des valeurs demi-entiers positifs:

$$ l = 0, 1/2, 1, 3/2, 2, \ldots \quad -l \le m \le l \,. $$

Il est important de remarquer que ce résultat, ainsi que les équations définissant l’action des opérateurs $L_\pm$ sur les états $\ket{lm}$ sont des conséquences exclusives de la forme algébrique des relations de commutation. Les valeurs de $l$ pour le moment angulaire, ou de $s$ pour le spin, dépendent des propriétés de transformation des états quantiques (la fonction d’onde) vis-à-vis de rotations. On sait que pour le spin de l’électron $s=1/2$, une valuer demi-entière. Concernant le moment angulaire $\bm L$, on doit imposer l’invariance de la fonction d’onde par rapport à une rotation de $2\pi$ autour de l’axe $z$,

$$ R_z(2\pi) \ket{lm} = \E^{-\I2\pi L_z} \ket{lm} = \E^{-\I2\pi m} \ket{lm} = \ket{lm}, $$

ce qui implique $m$ entier, $\E^{\I2\pi m}=1$ (la dernière égalité exprime l’invariance, $R_{\bm n}(2\pi) = 1$). On constante que cette symétrie impose bien $l$ entier:

$$ \begin{equation} \label{e:Llmentiers} l = 0, 1, 2, \ldots \quad -l \le m \le l \,. \end{equation} $$

On remarque également que l’espace de Hilbert d’un état de moment angulaire $l$, est un espace de dimension finie $2l+1$. Un spin $1/2$ a un espace de Hilbert de dimension $2=s(s+1)$, un orbital atomique de moment $l=1$, l’orbital p, est de dimension 3 (voir l’exemple dans le chapitre sur les symétries).

On signale enfin, que les propriétés du moment angulaire associées au principe d’exclusion de Pauli, selon lequel deux électrons ne peuvent pas occuper le même état quantique, permettent d’expliquer, en grande partie, la structure électronique des atomes telle qu’elle se manifeste par le tableau périodique des éléments de Mendeleïev.

Harmoniques sphériques

En représentation position l’opérateur du moment angulaire $\bm L = \bm x \wedge \bm p $ et sa valeur absolue $L^2$ s’écrivent, en utilisant $\bm p = -\I \nabla$ ($\hbar=1$), en coordonnées sphériques $(r,\theta,\phi)$,

$$ \begin{align} \label{e:LLx} L_x &= \I \left(\sin \phi \frac{\partial }{\partial \theta} + \frac{\cos \phi}{\tan \theta} \frac{\partial }{\partial \phi} \right) \nonumber\\ L_y &= \I \left( -\cos\phi \frac{\partial }{\partial \theta} + \frac{\sin\phi}{\tan \theta} \frac{\partial }{\partial \phi} \right) \\ L_z &= -\I \frac{\partial }{\partial \phi} \nonumber\,, \end{align} $$

$$ \begin{equation} \label{e:LLLx} L^2 = \frac{\partial }{\partial r}r^2 \frac{\partial }{\partial r} -r^2\nabla^2\,, \end{equation} $$

ce qui implique que les vecteurs propres de $L^2$ sont reliés aux fonctions propres du laplacien angulaire:

$$ - L^2 = \frac{1}{\sin \theta} \frac{\partial }{\partial \theta } \sin \theta \frac{\partial }{\partial \theta } + \frac{1}{\sin^2 \theta } \frac{\partial^2 }{\partial \phi^2}\,. $$

Les fonctions d’onde en coordonnées sphériques, paramétrées par la paire $l,m$, se définissent par le braket

$$ \begin{equation} \label{e:LY} Y_{lm}(\theta,\phi) = \braket{\theta, \phi| lm}, \; \end{equation} $$

dont les équations à valeurs propres sont,

$$ \begin{equation} \label{e:LYlm} L_z Y_{lm} (\theta,\phi) = \hbar m Y_{lm}(\theta,\phi), \quad L^2 Y_{lm}(\theta,\phi) = \hbar^2 l(l+1) Y_{lm}(\theta,\phi) \,. \end{equation} $$

En utilisant l’équation $\eqref{e:LLx}$ de la composante $z$ du moment angulaire, on déduit que les solutions de la première équation $\eqref{e:LYlm}$, sont des fonctions de la forme $Y_{lm}(\theta, \phi) = \E^{\I m \phi} f(\theta)$, avec $f$ déterminée par la deuxième équation. La condition d’invariance de la fonction d’onde, comme on l’a déjà démontré pour les états $\ket{lm}$, $Y_{lm}(\theta, \phi) = Y_{lm}(\theta, \phi + 2\pi)$, impose $m$ entier, et donc

$$ l=0,1,2,\ldots \quad |m| \le l . $$

Une propriété importante des fonctions $\eqref{e:LY}$ est qu’elles permettent de trouver une famille de solutions de l’équation de Laplace $\nabla^2 \psi(r,\theta,\phi) = 0$ régulières en $r=0$, de la forme

$$ \psi(r,\theta,\phi) = r^l Y_{lm}(\theta,\phi), $$

car, en remplaçant dans le laplacien on obtient, pour la partie radiale, le premier terme de $\eqref{e:LLLx}]$, $l(l+1)r^{l-2}$, formule identique et de signe contraire à celle du terme angulaire, calculée à partir de l’équation des valeurs propres $\eqref{e:LYlm}$.

La construction des harmoniques sphériques peut se faire d’une manière semblable à la construction des états d’énergie de l’oscillateur harmonique, pour lequel nous avons utilisé la fonction d’onde de l’état fondamental et l’opérateur de création pour obtenir les états excités. Un rôle semblable aux opérateurs $a$ et $a^\dag$ est joué par $L_-$ et $L_+$,

$$ \begin{equation} \label{e:LLpLmx} L_\pm = \E^{\pm \I \phi} \left( \pm \frac{\partial }{\partial \theta } + \I \cot \theta \frac{\partial }{\partial \phi} \right) \end{equation} $$

comme on peut le voir par les équations $\eqref{e:LLpLm}$. Étant donné par exemple l’état $\ket{ll}$, auquel l’application de $L_+$ donne zéro $L_+ \ket{ll} = 0$,

$$ \E^{\I \phi} \left( \frac{\partial }{\partial \theta } + \I \cot \theta \frac{\partial }{\partial \phi} \right) \E^{\I l \phi} f(\theta) = 0 $$

par application successive de $L_-$ on peut obtenir l’ensemble d’états $\ket{lm}$, $-l \le m \le l$. La solution de l’équation précédente est

$$ f(\theta) = c_{ll} \sin^l \theta \,, $$

à une constante de normalisation près, $c_{ll}$, qu’on détermine par la condition de normalisation des états $\braket{\theta,\phi|lm}$. L’état $\ket{l, l-1}$ est donc obtenu à partir de

$$ \braket{\theta,\phi | l,l-1 } = c_{ll} \E^{-\I \phi} \left(- \frac{\partial }{\partial \theta } + \I \cot \theta \frac{\partial }{\partial \phi} \right) \E^{\I l \phi} \sin^l \theta $$

$$ Y_{l,l-1} = c_{l,l-1} \E^{\I(l-1) \phi}\sin^{l-1}\theta \cos \theta\,. $$

Par itération, et après quelques manipulations algébriques,% % \footnote{Voir le livre de Cohen-Tannoudji et al. \cite{Cohen-Tannoudji-1973db}, chapitre IV, complément A.} % on obtient les harmoniques sphériques:

$$ \begin{equation} \label{e:LYformule} Y_{l,m}(\theta, \phi) = c_{lm} \E^{\I m \phi} \sin^{-m} \theta \left( \frac{\D}{\D \cos \theta } \right)^{l-m} \sin^{2l}\theta \quad 0 \le m \le l \end{equation} $$

avec les constantes de normalisation

$$ c_{lm} = \frac{(-1)^{m}}{2^ll!} \left( \frac{(l+m)! (2l+1)}{4\pi (l-m)!} \right)^{1/2}\,. $$

Pour les $m<0$ on utilise la relation,

$$ \begin{equation} \label{e:LYmm} Y_{l, -m}(\theta,\phi) = (-1)^m Y^*_{lm}(\theta,\phi)\,,\quad m > 0\,. \end{equation} $$

La forme des constantes $c_{lm}$ garantie l’orthonormalité des harmoniques sphériques:

$$ \begin{equation} \label{e:LYortho} \int_{0}^{2\pi} \D \phi \int_{0}^{\pi} \D \theta \sin\theta\, Y^*_{lm}(\theta,\phi) Y_{l'm'}(\theta,\phi) = \delta_{ll'} \delta_{mm'}\,. \end{equation} $$

Si on y ajoute la relation de fermeture:

$$ \begin{equation} \label{e:LYdelta} \sum_{lm} Y_{lm}(\theta,\phi) Y_{lm}(\theta',\phi') = \delta(\theta-\theta')\delta(\phi-\phi') \end{equation} $$

on déduit que toute fonction des angles sphériques peut s’écrire comme superposition des $Y$:

$$ \begin{equation} \label{e:LYsum} f(\theta,\phi) = \sum_{lm} f_{lm} Y_{lm}(\theta,\phi)\,. \end{equation} $$

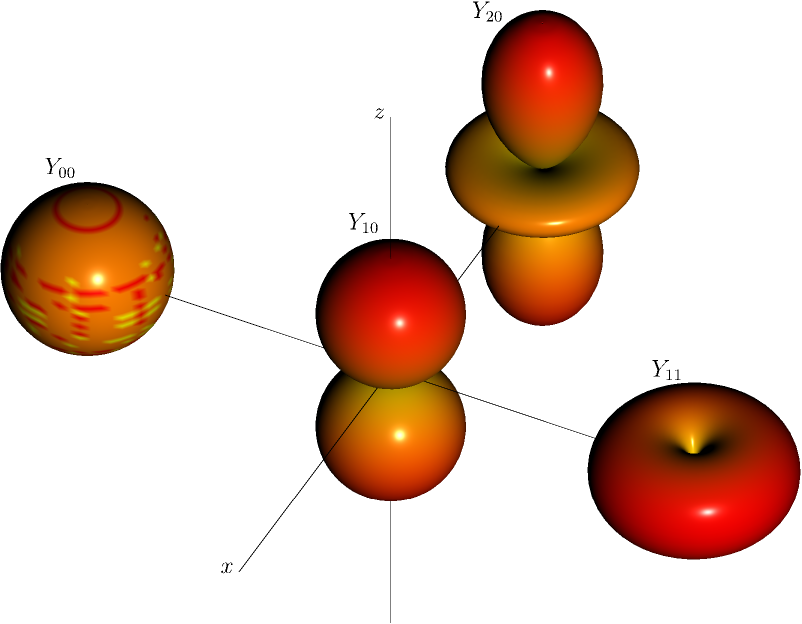
Harmoniques sphériques $Y_{lm}(\theta,\phi)|$ pour $(l,m)=(0,0)$, $(1,0),(1,1)$, et $(2,0)$.

# numpy, scipy, matplotlib
import numpy as np
import scipy
from scipy.special import sph_harm
import matplotlib.pylab as plt
# spherical harmonic Y_lm
l, m = 3, 0
phi = np.linspace(0,2*np.pi, 65)
theta = np.linspace(0,np.pi, 65)
theta, phi = np.meshgrid(theta, phi) # spherical lattice
# figure
fig, ax = plt.subplots(figsize=(8,8), subplot_kw={'projection': '3d'})
# scipy Y_lm
Ylm = sph_harm(m, l, phi, theta)
Y = np.abs(Ylm)
# map to cartesian coordinates
x = Y * np.cos(phi) * np.sin(theta)
y = Y * np.sin(phi) * np.sin(theta)
z = Y * np.cos(theta)
# plot
ax.plot_surface(x, y, z, cmap='RdBu', alpha=0.7)
ax.set_aspect(aspect='equal')
ax.axis('off')
plt.show();

Les expressions explicites des harmoniques sphériques pour les premières valeurs de $l$, $l=0,1,2$ sont

$$ \begin{align} Y_{00}(\theta,\phi) & = \frac{1}{\sqrt{4\pi}} \nonumber\\ Y_{10}(\theta,\phi) & = \sqrt{\frac{3}{4\pi}} \cos\theta \nonumber\\ Y_{1,\pm1}(\theta,\phi) & = \mp \sqrt{\frac{3}{8\pi}} \sin\theta\, \E^{\pm\I\phi} \nonumber \\ Y_{20}(\theta,\phi) & = \sqrt{\frac{5}{16\pi}} (3\cos^2\theta - 1) \nonumber\\ Y_{2,\pm1}(\theta,\phi) & = \mp \sqrt{\frac{15}{8\pi}} \sin\theta \cos\theta\, \E^{\pm\I\phi} \nonumber \\ Y_{2,\pm2}(\theta,\phi) & = \sqrt{\frac{15}{32\pi}} \sin^2\theta\, \E^{\pm 2 \I \phi} \label{e:LY012} \end{align} $$

La figure et l’exemple de code python montrent le graphe et le calcul de quelques harmoniques sphériques en fonction des angles $\theta, \phi$.

Application: addition de deux spins 1/2

Une question intéressante se pose à propos de la composition de spins. On a vu que les composantes du moment angulaire ne sont pas de observables compatibles; en plus, le moment angulaire est quantifié: seules quelques valeurs discrètes sont possibles pour sa “longueur” et composante “z”. De lors, comment décrire un système de deux spins? On se propose maintenant d’étudier, en commençant par l’identification des observables pertinents, le spin d’un système composite formé de deux spins (combinaison de deux électrons, par exemple).

L’espace de hilbert $\mathcal{H}$ de deux spins est le produit tensoriel (de kronecker) des espaces vectoriels d’un spin $\mathcal{H}_1$:

$$ \mathcal{H} = \mathcal{H}_1 \otimes \mathcal{H}_1. $$

Les observables, les opérateurs de spin pour chaque spin ont aussi une structure tensorielle:

$$ \bm S_1 = \bm S \otimes \mathbb{I}, \quad \bm S_2 = \mathbb{I} \otimes \bm S $$

avec $\mathbb{I}=1_2$ l’opérateur identité de dimension 2. Cette structure tensorielle permet de définir naturellement l’opérateur de spin total $\bm S$ comme étant simplement la somme de deux vecteurs:

$$ \bm S = \bm S_1 + \bm S_2 = \frac{1}{2}\big( \bm \sigma \otimes \mathbb{I} + \mathbb{I} \otimes \bm \sigma) $$

($\hbar =1$) avec $\bm \sigma = (\sigma_x, \sigma_y, \sigma_z)$ le vecteur de matrices de pauli:

$$ \sigma_x = \begin{pmatrix}0&1\\1&0\end{pmatrix}, \; \sigma_x = \begin{pmatrix}0&-\I\\\I&0\end{pmatrix}, \; \sigma_x = \begin{pmatrix}1&0\\-1&0\end{pmatrix}. $$

Comme $\bm S$ est lui même un moment angulaire, on peut définir une base $\ket{s,m}$ par

$$S^2 \ket{sm} = s(s+1) \ket{sm}, \; S_z \ket{sm} = m \ket{sm},\quad s=0,1/2,1,\ldots,\; -s\le m \le s $$

où EX

$$ S^2 = \frac{3}{2} \mathbb{I} + \frac{1}{2} \bm \sigma_1 \cdot \bm \sigma_2, \quad S_z = \frac{1}{2} \sigma_{1z} + \frac{1}{2} \sigma_{2z}. $$

En forme matricielle on obtient,

$$ \sigma_1 \cdot \sigma_2 = \begin{pmatrix}1 & 0 & 0 & 0 \\ 0 & -1 & 2 & 0 \\ 0 & 2 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}, \quad S_z = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}. $$

On va maintenant déterminer les possibles valeurs de $s$ et $m$. La diagonalisation de $S^2$ donne le spectre

$$ \{\{s(s+1),\ket{sm}\}\} = \{\{0,\ket{0,0}\}, \{2,\ket{1,-1}, \ket{1,0}, \ket{1,1}\}\} $$

($2=1\times(1+1)$) avec $s=1$ l’état “triplet” triplement dégénéré et $s=0$ l’état “singulet”, et les vecteurs propres

$$ \ket{0,0} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0\\1\\-1\\0 \end{pmatrix},\; \ket{1,-1} = \begin{pmatrix} 0\\0\\0\\1 \end{pmatrix},\; \ket{1,0} = \frac{1}{\sqrt{2}} \begin{pmatrix} 0\\1\\1\\0 \end{pmatrix},\; \ket{1,1} = \begin{pmatrix} 1\\0\\0\\0 \end{pmatrix}. $$

Les quatre états $\ket{jm}$ forment une base orthonormale de $\mathcal{H}$, et la matrice formée avec ces colones ($V$ dans le code python, ci-bas) est la matrice unitaire de passage entre la base canonique du produit $\mathcal{H}_1 \otimes \mathcal{H}_1$ et celle du système composite, associée aux observables $S^2,S_z$.

Exemple de code sympy/python (méthode diagonalize()) pour le calcul du spectre de $\ket{S}$.

# sympy
import sympy as sy
from sympy.physics.quantum import TensorProduct as K
# pauli matrices
X = sy.Matrix([[0,1],[1,0]])
Y = sy.Matrix([[0,-sy.I],[sy.I,0]])
Z = sy.Matrix([[1,0],[0,-1]])
id = sy.Matrix([[1,0],[0,1]])
# two spins S^2 and S_z matrices
ss = K(X,X) + K(Y,Y) + K(Z,Z) # $\sigma_1 \cdot \sigma_2$
s2 = 3*K(id,id)/2 + ss/2 # $S^2$
s2z = (K(Z,id) + K(id,Z))/2 # $S_z$
# spectre V = \{\ket{sm}\}$ (vectors) and D (eigenvalues)
V, D = s2.diagonalize()
# verify that $\ket{sm}$ is also eigenvector of $S_z$
[s2z*V[:,i] for i in range(4)]

Ainsi, la composition de deux spins $1/2$ résulte en un spin $0$ (singulet) ou $1$ (triplet). L’état singulet est antisymétrique, puisqu’en échangeant les deux spins le état change de signe, tandis que le triplet est symétrique.

On observe que dans la base $\ket{s,m}$ l’opérateur

$$ \bm \sigma_1 \cdot \bm \sigma_2 = S^2 - 3 \mathbb{I} $$

est diagonal, proportionnel à $2s(s+1) \mathbb{I} + 3 \mathbb{I}$, par conséquent

$$ P_0 = \frac{\mathbb{I} - \bm \sigma_1 \cdot \sigma_2}{4}, \quad P_1 = \frac{3\mathbb{I} + \bm \sigma_1 \cdot \sigma_2}{4}, \quad $$

sont de projecteurs, dans l’espace de deux spins, sur les sous-espaces de spin total 0 et 1, respectivement.

Contrairement à ce qu’on pourrait naïvement penser, l

Potentiel central

Le mouvement d’une particule quantique dans un potentiel à symétrie sphérique est décrit par le hamiltonien

$$ \begin{equation} \label{e:rH} H = -\frac{\hbar^2}{2mr^2} \frac{\partial }{\partial r}r^2 \frac{\partial }{\partial r} + \frac{L^2}{2mr^2} + V(r) \end{equation} $$

(en représentation position et en coordonnées sphériques $(r,\theta,\phi)$). Le fait que l’interaction ne dépende que du rayon $r$, et non des variables angulaires, permet d’écrire la fonction d’onde $\psi=\psi(r,\theta,\phi)$ comme un produit,

$$ \begin{equation} \label{e:rpsi} \psi(r,\theta,\phi) = f(r) Y_{lm}(\theta,\phi) \end{equation} $$

et de séparer les variables. L’équation de Schrödinger $H\psi=E\psi$, pour cette fonction d’onde est,

$$ \begin{equation} \label{e:rSch} -\frac{\hbar^2}{2m} \left[ f''(r) + \frac{2}{r} f'(r) \right] + V_\text{eff}(r) f(r) = E f(r) \end{equation} $$

où nous avons introduit le potentiel effectif

$$ V_\text{eff}(r) = \frac{\hbar^2 l(l+1)}{2mr^2} + V(r)\,, $$

et noté les dérivées radiales par des primes.

Le puits sphérique

On considère une particule de masse $m$ confinée dans une sphère de rayon $a$. Le potentiel est supposé infini à l’extérieur de la sphère:

$$ V(r) = \begin{cases}0 & r<a \\ \infty & r>0\end{cases}. $$

On doit donc résoudre, pour $r<a$, l’équation radiale

$$ f''(r) + \frac{2}{r} f'(r) + \Big(k^2 - \frac{l(l+1)}{r^2}\Big) f(r) = 0, $$

avec $k^2=2mE$. C’est l’équation différentielle des fonctions de Bessel sphériques:

$$ f(r) = A j_l(kr) + B y_l(kr), $$

où $j_l,y_l$ sont les fonctions de premier et seconde espèce, elles sont proportionnelles aux fonctions de bessel $J_l,Y_l$ d’ordre demi-entier. Voici quelques exemples:

$$ \begin{gather*} j_0 = \frac{\sin x}{x}, \quad y_0 = -\frac{\cos x}{x}\\ j_1 = \frac{\sin x}{x^2} - \frac{\cos x}{x}, \quad n_1 = -\frac{\cos x}{x^2} - \frac{\sin x}{x} \\ j_l(x) \sim x^l \; (x \ll 1), \quad n_l(x) \sim \frac{1}{x^l} \; (x \ll 1)\\ j_l(x) \sim \frac{\sin(x-\pi l/2)}{x} \; (x\gg1), \quad y_l(x) \sim -\frac{\cos(x-\pi l/2)}{x} (x \gg 1). \end{gather*} $$

Comme la fonction d’onde doit être régulière à l’origine on trouve $B=0$ ($y_l$ diverge a l’origine). En plus, la fonction d’onde doit s’annuler à l’extérieur, ce qui implique $f(a) = 0$; cette condition se traduit par la quantification du nombre d’onde:

$$ ka = z_{nl} $$

avec $z_{nl}$ le $n$-ième zéro de $j_l$.

En conclusion, les niveaux d’énergie de la particule sont:

$$ E_{nl} = \frac{\hbar^2}{2ma^2} z^2_{nl}, $$

et la fonction d’onde, qui dépend des nombre quantique $n$ (énergie) et $l$ (orbital) est

$$ \psi(r,\theta,\phi) = A j_l(z_{nl}r/a) Y_{lm}(\theta,\phi), $$

où $A = A_{nl}$ est la constante de normalization.

Zéros de $j_l(x)$ pour $l=0,1,2,3$.

L’atome d’hydrogène

Dans le cas de l’atome de l’hydrogène ou des ions avec un seul électron, le potentiel effectif contient, en plus du terme dû au moment angulaire, l’interaction coulombienne de l’électron avec le proton:

$$ V(r) = -\frac{e^2}{4\pi \epsilon_0 r} $$

ou $e$ est la charge élémentaire.

Potentiel effectif de l’atome de Bohr $V(r)=1/r^2 - 2/r$. La ligne grise représente le potentiel quantique $V_\text{eff}$ pour $l=1$.

Le potentiel effectif devient (voir figure ci-dessus),

$$ \begin{equation} \label{e:rVeff} V_\text{eff}(r) = \frac{\hbar^2 l(l+1)}{2mr^2} - \frac{e^2}{4\pi \epsilon_0 r}, \end{equation} $$

qu’on peut généraliser pour d’autres atomes hydrogénoïdes en remplaçant $e$ par $Ze$, avec $Z$ le nombre de protons.

Par analogie avec le modèle de Bohr, dans lequel le potentiel effectif:

$$ V_\text{Bohr}(r)= \mathrm{Ry} \left(\frac{a_0^2}{r^2} - \frac{2a_0}{r} \right), $$

possède un minimum au rayon de Bohr $r=a_0$ d’énergie $E_1=-\mathrm{Ry}$ un Rydberg, on s’attend à ce que l’atome d’hydrogène possède aussi une série d’états liés aux énergies négatives $E<0$. On remarque toutefois que le potentiel de Bohr diffère du potentiel effectif quantique par la dépendance de celui-ci sur le moment angulaire en $l(l+1)$. Le principe d’incertitude interdit un état quantique au minimum de l’énergie potentielle, ce qui reviendrait à fixer simultanément l’énergie potentielle et l’énergie cinétique.

Il convient de réduire les dimensions en utilisant la masse de l’électron $m$ (ou masse effective du problème à deux corps) comme unité de masse, le rayon de Bohr $a_0$ comme unité de longueur et enfin le Rydberg $\mathrm{Ry}$ comme unité d’énergie:

$$ a_0= \hbar^2/mq^2\,, \quad \mathrm{Ry} = q^2/2 a_0\,, \quad q^2 = e^2/4\pi\epsilon_0\,. $$

L’équation pour la fonction radiale $\eqref{e:rSch}$ s’écrit dans ce système d’unités,

$$ \begin{equation} \label{e:rSchd} f''(\rho) + \frac{2}{\rho} f'(\rho) + \left[ -\frac{1}{4} + \frac{n}{\rho} - \frac{l(l+1)}{\rho^2} \right] f(\rho) = 0\,, \end{equation} $$

$$ \rho = \frac{2r}{n}, \quad n = \frac{1}{\sqrt{-E}}\,, $$

avec $n$ un nombre à determiner, en principe un réel pour les niveaux d’énergie négative $E<0$ correspondants aux états liés, et avec $f'$ la dérivée de $f$ par rapport à $\rho$.

Il est facile d’identifier le comportement asymptotique de $f$: pour les petits $\rho\ll 1$ on peut négliger les termes en $O(1)$ et $O(1/\rho)$,

$$ f''(\rho) - \frac{l(l+1)}{\rho^2}=0 \; \Rightarrow \; f(\rho) \sim \rho^l\,; $$

et pour les grands $\rho\gg1$, on peut ne retenir que le bilan du terme constant avec la dérivée deuxième,

$$ f''(\rho) - \frac{f(\rho)}{4} = 0 \; \Rightarrow \; f(\rho) \sim \E^{-\rho/2}\,, $$

la solution en $\E^{\rho/2}$, étant divergente ne correspond pas à un état quantique. Regroupant les deux comportements, près de l’origine et près de l’infini, l’ansatz $f(\rho) = \rho^l \E^{-\rho/2}w(\rho)$ conduit à une équation différentielle pour la fonction $w(\rho)$ de la forme,

$$ \begin{equation} \label{e:rW} \rho w'' + (2l + 2 - \rho) w' + (n -l -1) w = 0 \,, \end{equation} $$

qu’on peut comparer à l’équation du polynôme de Laguerre généralisés $L_q^p$:

$$ \begin{equation} \label{e:rLag} x y'' + (p + 1 - x) y' + q y = 0 \; \Rightarrow \; y = L_q^p(x)\,, \end{equation} $$

pour conclure que la fonction radiale est proportionnelle aux polynômes de Laguerre $f\sim L$. En effet, la solution générale de $\eqref{e:rW}$ s’exprime par des fonctions hypergéométrique, lesquelles ne divergent pas exponentiellement vite à l’infini que pour des valeurs entiers positifs de $q=n-l-1$:

$$ \begin{equation} \label{e:rn} n = 1,2, \ldots \quad 0\le l \le n-1 \end{equation} $$

ce qui implique des niveaux d’énergie discrets:

$$ \begin{equation} \label{e:rEn} E = - \frac{1}{n^2} \,. \end{equation} $$

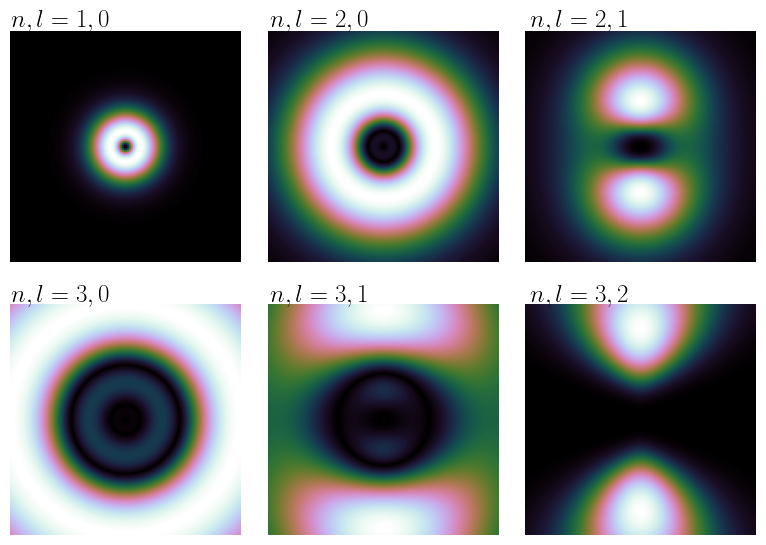
Carré des orbitales radiales $p_{nl}(r) = r^2R_{nl}^2(r)$ (normalisés à leur maximum) pour quelques valeurs de $\{n,l\}$.

Dans ce cas la solution hypergéométrique se réduit à un polynôme. La fonction radiale s’écrit enfin comme $f = R_{nl}(r)$:

$$ \begin{equation} \label{e:rRnl} R_{nl}(r) = c_{nl} \left( \frac{2}{n} \right)^{\tfrac{3}{2}} \left(\frac{2r}{n}\right)^l \E^{-\tfrac{r}{n}} L_{n-l-1}^{2l+1} \left(\frac{2r}{n}\right) \end{equation} $$

avec la constante assurant la bonne normalisation de l’état quantique,

$$ c_{nl} = \sqrt{ \frac{(n-l-1)!}{2n[(n+l)!]^3} } \,. $$

En unités SI:

$$ \begin{equation} \label{e:rRsi} R_{nl}(r) = c_{nl} \left(\frac{2Z}{na_0}\right)^{\tfrac{3}{2}} \left(\frac{2Zr}{na_0}\right)^l \E^{-\tfrac{Zr}{na_0}} L_{n-l-1}^{2l+1} \left(\frac{2Zr}{na_0}\right) \end{equation} $$

et les niveaux d’énergie correspondants sont,

$$ \begin{equation} \label{e:rEsi} E_n = -\frac{Z^2 \mathrm{Ry}}{n^2}\,. \end{equation} $$

Les premiers fonctions radiales sont:

$$ \begin{equation} R_{10} = 2 \E^{-r}, \quad R_{20} = \frac{1}{\sqrt{2}} \E^{-r/2} \left(1-\frac{r}{2}\right), \quad R_{21} = \frac{1}{2\sqrt{6}} \E^{-r/2} r \,. \label{e:rR12} \end{equation} $$

L’équation $\eqref{e:rEsi}$ reproduit avec une précision remarquable les données spectroscopiques de l’atome d’hydrogène (séries spectrales de Lyman et de Balmer). Pour les énergies positives le spectre de l’atome d’hydrogène est continu; il correspond aux états de l’atome ionisé, où l’électron de valence est libre.

Densité de probabilité $r^2|R_{lm}(r) Y_{lm}(\theta,\phi)|^2 $, dans le plan $xz$, pour quelques valeurs de $\{n,l\}$, avec $m=0$. Le côté du carré est de $2\times 15\,a_0$.

La fonction d’onde de l’électron d’un atome d’hydrogène est caractérisé par trois nombres quantiques $n,l,m$, nommés principal, azimuthal ou orbital et magnétique, respectivement:

$$ \begin{equation} \label{e:rFO} \psi_{nlm}(r,\theta,\phi) = \braket{r \theta \psi|n l m} = R_{nl}(r)Y_{lm}(\theta, \psi) \end{equation} $$

où $\ket{nlm}$ est une base de l’espace de Hilbert des états liés. Chaque niveau d’énergie de nombre principal $n$ est dégénéré $2l+1$ fois, avec $l$ le nombre orbital $0\le l \le n-1$, selon les différentes valeurs de $m$, le nombre quantique magnétique; la dégénérescence totale des premiers $n$ niveaux est $n^2$:

$$ \begin{equation} \label{e:rDeg} \sum_{l=0}^{n-1}(2l+1) = n^2 \,. \end{equation} $$

L’action d’un champ extérieur, comme un champ électrique ou un champ magnétique, peuvent révéler la structure fine des lignes spectrales en levant la dégénérescence et séparent les lignes d’un même $l$. Outre la dégénérescence orbitale, y il a une dégénérescence de spin: chaque niveau $\ket{nlm}$ possède deux possibles polarisations du spin, ce qui ajoute un facteur 2 à la formule $\eqref{e:rDeg}$, $2n^2$.