$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}{\boldsymbol}$

Cours de mécanique quantique.

Principes de la mécanique quantique

L’état d’un système quantique correspond à un vecteur $\ket{\psi}$ de norme 1 de l’espace de Hilbert $\mathcal{H}$:
$$ \begin{equation} \ket{\psi} \in \mathcal{H}, \end{equation} $$
cette état constitue une description complète du système physique.

Le fait que l’état quantique puisse être associé à un vecteur d’un espace vectoriel linéaire sur les complexes est une conséquence du principe de superposition: expérimentalement on observe des effets d’interférence quantique, comme dans l’expérience de deux fentes dans laquelle apparaît sur le détecteur (écran) un motif d’interférence similaire à celui d’une onde électromagnétique mais produit par, par exemple, un faisceau de neutrons, ou dans l’expérience de Stern-Gerlach où on mesure l’état de spin d’un électron. Dans le premier cas il s’agit d’une superposition de chemins: l’état du neutron résulte d’une superposition de “chemins” entre la source et l’écran, passant par chaque fente. Dans le second cas, l’état $\ket{\psi}$ de spin de l’électron (atomes d’argent dans l’expérience) se présente comme étant la superposition d’un spin “up” $\ket{0}$, et d’un spin “down” $\ket{1}$:

$$\ket{\psi} = a \ket{0} + b \ket{1},$$

avec $|a|^2 + |b|^2 = 1$.

L’espace des états $\mathcal{H}$ d’un ensemble de système quantiques $\{1,2,\ldots, N\}$ est un espace de hilbert obtenu par le produit tensoriel (Kronecker) des espaces de hilbert de chaque partie $n$:
$$ \begin{equation} \mathcal{H} = \bigotimes_n \mathcal{H}_n,\quad n = 1, 2, \ldots, N \end{equation} $$
L’état d’un système quantique composite est décrit par l’opérateur densité (ou matrice densité, pour un espace de dimension finie)
$$ \begin{equation} \rho = \sum_n p_n \ket{\psi_n} \bra{\psi_n}, \quad \sum_n p_n = 1 \end{equation} $$
où $\ket{\psi_n}$ est l’état de $n$ avec probabilité $p_n$.

La matrice densité satisfait EX: - $\Tr \rho = 1$ (trace 1, normalisation) - $\rho = \rho^\dagger$ (hermitienne) - $\braket{\psi| \rho |\psi} \ge 0$ pour $\ket{\psi}$ arbitraire (positive)

Une source de photons non-polarisée est un exemple de système composite: chaque photon a une certaine probabilité de se trouver dans un état particulier, lui même superposition des états de base de polarisation donnée. La matrice densité décrit donc un mélange statistique de systèmes quantiques.

Si $\ket{b_n}$ est une base de $\mathcal{H}_n$, le principe de superposition implique

$$ \ket{\psi} = \sum_{b_1 b_2 \ldots } \psi_{b_1 b_2 \ldots} \ket{b_1}\otimes\ket{b_2}\otimes \ldots \in \mathcal{H} $$

Une conséquence immédiate de cette expression est qu’on ne peut généralement pas écrire l’état de la partie $A = \{1, 2, \ldots, N_A\}$, bipartition du système global $AB$, comme un ket de $\mathcal{H}_A$ EX. Par conséquent l’état d’un sous-système d’un système quantique dans un état pur est un état composite. Il est donné par la trace partielle

$$ \rho_A = \Tr_{\bar{A}} \ket{\psi} \bra{\psi} $$

où $B = \bar{A}$ est le complément de l’ensemble $A$.

On en déduit qu’il est toujours possible de “compléter” l’espace de hilbert d’un état mixte $\rho$ pour le transformer en état pur $\ket{\psi}$ de sorte que la trace partielle du système étendu soit justement $\rho$ du “sous-système”.

L’état du sous-système $A$, ne peut généralement pas s’écrire sous la forme d’un ket de $\mathcal{H}_A$; ceci serait possible si l’état du système global $\ket{\psi}$ était simplement le produit tensoriel des états de chaque sous-système $\ket{\psi}= \ket{\psi_A} \otimes \ket{\psi_B}$. L’impossibilité d’exprimer un état pur comme un produit indique que cet état est intriqué. L’état d’un sous-système d’un état intriqué est donc un état mixte décrit par une matrice densité.

Une observable $O$ (grandeur physique) correspond à un opérateur hermitien sur l’espace de hilbert des états $\mathcal{H}$:
$$ \begin{equation} O = O^\dagger \end{equation} $$
Les valeurs propres $o_n$
$$ \begin{equation} O \ket{o_n} = o_n \ket{o_n} \end{equation} $$
sont les résultats possibles d’une mesure de $O$. Les vecteurs propres $\ket{o_n}$ forment une base orthonormale
$$ \braket{o_n|o_m} = \delta_{nm}, \quad \sum_n P_n = 1, \quad P_n = \ket{o_n}\bra{o_n},> $$
de l’espace de hilbert; les opérateur $P_n$ sont de projecteurs sur les “directions” de vecteurs propres $\ket{o_n}$. La valeur espérée de $O$ dans l’état $\ket{\psi}$ est
$$ \braket{O} = \braket{\psi|O|\Psi} $$

La mesure de l’état $\ket{\psi} \in \mathcal{H}$ donne le résultat $o_n$ avec probabilité (règle de Born):

$$ \begin{equation} \mathrm{Prob}(o = o_n) = p_n = \big|\braket{o_n|\psi}\big|^2. \end{equation} $$

Une forme équivalente en fonction de l’opérateur de projection $P_n$ est

$$ p_n = \braket{\psi|P_n|\psi}, $$

la probabilité d’obtenir $o_n$ dans l’état $\ket{\psi}$ correspond donc à la valeur espérée du projecteur sur le vecteur propre $\ket{o_n}$ dans cet état.

L’état du système, après la mesure, est “réduit”:

$$ \ket{\psi} \rightarrow \frac{\braket{o_n|\psi}}{\sqrt{p_n}}\ket{o_n}. $$

La règle de Born se généralise facilement au cas d’un système mixte, décrit par la matrice densité $\rho$. La valeur espérée d’un observable $O$ devient

$$ \braket{O} = \Tr\, \rho O. $$

On vérifie que pour un état pur $\psi$ on retrouve la bonne expression: $\Tr \big(\ket{\psi}\bra{\psi} O \big) = \braket{\psi|O|\psi}$. En remplaçant $O$ par un projecteur on obtient la probabilité (Born):

$$ p_n = \Tr\, \rho P_n, $$

qui vérifie $\sum_n p_n = 1$. L’état, après la mesure, devient

$$ \rho_n = \frac{P_n\rho P_n}{\Tr \, \rho P_n}. $$

L’évolution d’un système quantique est unitaire:
$$ \begin{equation} \ket{\psi(t)} = U(t, t_0) \ket{\psi(t_0)}, \quad U^\dagger U = 1 \end{equation} $$
où le “temps” $t$ est un paramètre réel (ou entier si la dynamique est discrète), $t_0$ est une référence (temps initial). Plus généralement toute transformation d’un état quantique dans un autre état quantique est une transformation unitaire.

La dynamique d’un système quantique est générée par le hamiltonien $H$ du système:

$$ U(t, t_0) = \E^{-\I H (t-t_0)} \quad (\hbar = 1). $$

L’état quantique satisfait par conséquent l’équation de Schrödinger

$$ \begin{equation} \I \frac{\partial}{\partial t} \ket{\psi(t)} = H \ket{\psi(t)}, \end{equation} $$

avec $\ket{\psi(t_0)}$ l’état initial.

Pour un système composite on a

$$ \rho(t) = U(t,t_0) \rho(t_0) U^\dagger(t, t_0). $$

Le principe de correspondance permet d’obtenir le hamiltonien d’un système quantique à partir de son équivalent “classique”; par exemple, le hamiltonien d’une particule $H(x,p)$, avec $x$ la position et $p$ l’impulsion, devient le hamiltonien quantique

$$ H(x,p), \quad [x, p] = \I, $$

dans lequel on a remplacé la position et l’impulsion par des opérateurs dont le commutateur n’est pas nul. En fait, il existe une analogie entre les équation de hamilton de la mécanique classique et la dynamique quantique en représentation de heisenberg; cette analogie conduit à l’identification du croche de poisson avec le commutateur quantique (Dirac):

$$\{Q, P\} \rightarrow \frac{1}{\I} [Q,P], $$

pour deux grandeurs conjuguées canonique $Q$ et $P$ et ces pendants quantiques les opérateurs $Q$ et $P$ (même notation).

Enfin, une propriété fondamentale de l’état quantique $\rho$ d’un système (mixte ou pur) est qu’on peut lui toujours associer une entropie:

$$ S[\rho] = - \Tr\, \rho \ln \rho. $$

C’est l’entropie introduite initialement par von Neumann pour caractériser le processus quantique de la mesure. Dans le cas ou $\rho = \rho_A$ représente l’état d’un partie $A$ d’un système bipartite $AB$, $S$ est une mesure de l’intrication de l’état total $\rho_{AB}$.

Compléments mathématiques

Espace vectoriel et produit scalaire

Soient $\ket{\psi}, \ket{\phi}, \ldots \in \mathcal{H}$ des vecteurs (kets en notation de Dirac) de l’espace vectoriel hilbertien $\mathcal{H}$ sur les complexes, et $a, b, \ldots \in \mathbb{C}$ des nombres complexes. On a donc

$$ a \ket{\psi} + b \ket{\phi} \in \mathcal{H}, $$

toute combinaison linéaire des vecteurs de $\mathcal{H}$ est en $\mathcal{H}$.

À tout ket $\ket{\psi} \in \mathcal{H}$ correspond un bra $\bra{\psi} \in \mathcal{H}^\dagger$ appartenant à l’espace dual. La notation $\cdots^\dagger$ indique l’adjoint (conjuguaison hermitienne). L’espace dual est tel que le produit (produit scalaire) d’un bra par un ket est un nombre complexe:

$$ \braket{\phi | \psi} = \braket{\psi|\phi}^\star \in \mathbb{C} $$

où $\cdots^\star$ est le complexe conjugué. Notez qu’on doit faire

$$ (a \ket{\psi})^\dagger = a^\star \bra{\psi}, \quad a \in \mathbb{C}. $$

La norme d’un vecteur $\ket{\psi}$ est $\sqrt{\braket{\psi | \psi}}$. Par exemple,

$$ \braket{\psi | \psi} = |a|^2 + |b|^2 = 1, \quad \ket{\psi} = a \ket{0} + b \ket{1} $$

avec $\{\ket{0}, \ket{1}\}$ orthonormés.

Une base $\ket{n}$ ($n=0,1,\ldots$) orthonormée et complète de l’espace de hilbert satisfait

$$ \braket{n|m} = \delta_{n,m}, \quad \sum_n \ket{n} \bra{n} = 1 $$

avec $1$ l’opérateur identité (unité) et $\delta_{n,m}$ la delta de kronecker. Le nombre de vecteurs dans la base est la dimension de l’espace de hilbert (elle peut bien sûr être infinie).

Tout vecteur se décompose sur les vecteurs de la base

$$ \ket{\psi} = \sum_n \psi_n \ket{n}, \quad \psi_n = \braket{n|\psi} \in \mathbb{C}, $$

où les $\psi_n$ sont les “amplitudes” (composantes). Notez que la normalisation de l’état impose

$$ \braket{\psi | \psi} = 1 \Rightarrow \sum_n |\psi_n|^2 = 1. $$

On dit que le vecteur formé avec les $\psi_n$ est une représentation dans la base $\ket{n}$ du ket $\ket{\psi}$:

$$ \ket{\psi} \doteq \begin{pmatrix} \psi_0 \\ \psi_1 \\ \vdots \end{pmatrix} $$

Applications linéaires

Un opérateur sur l’espace de hilbert est une application linéaire

$$ A: \mathcal{H} \times \mathcal{H} \rightarrow \mathcal{H}, $$

tel que

$$ A \ket{\psi} \in \mathcal{H}, \quad \forall \ket{\psi} \in \mathcal{H}. $$

Le symbol $\times$ indique le produit cartésien (à distinguer du produit de kronecker $\otimes$). L’ensemble de nombres

$$ A_{mn} = \braket{m | A | n} \in \mathcal{C} $$

constituent une représentation de l’opérateur $A$ sous la forme d’une matrice: $m$ désigne la ligne et $m$ la colonne:

$$ A \doteq \begin{pmatrix} A_{00} & A_{01} & \cdots \\ A_{10} & A_{11} & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix}. $$

L’adjoint ou complexe hermitien d’un opérateur est défini par la relation

$$ \braket{\phi |A^\dagger |\psi} = \braket{\psi |A |\phi}^\star . $$

Notez

$$ (AB)^\dagger = B^\dagger A^\dagger. $$

Un opérateur est hermitien ou auto-adjoint si $O = O^\dagger$; ses éléments de matrice satisfont donc $O_{mn} = O_{nm}^\star$ (le transposé conjugué). Tout opérateur hermitien possède un spectre réel (valeurs propres $o_n$), et ses vecteur propres $\ket{o_n}$ forment une base orthonormée:

$$ O \ket{o_n} = o_n \ket{o_n}. $$

Un opérateur est unitaire si son inverse est son adjoint $U^{-1} = U^\dagger$; on a donc $UU^\dagger = U^\dagger U = 1$. Il est toujours possible de diagonaliser un opérateur hermitien par une transformation unitaire de la base:

$$ O = U D U^\dagger, \quad D = \mathrm{diag}(o_0, o_1, \ldots). $$

L’opérateur (matrice) $U$ est l’opérateur de changement de base.

En effet, l’application linéaire pour passer d’une base orthonormée $\ket{n}$ à une autre base orthonormée $\ket{n'}$ est un opérateur unitaire $U$:

$$ \ket{n'} = U \ket{n} \, \Rightarrow \, U = \sum_n \ket{n'} \bra{n}\,. $$

On voit qu’effectivement $U$ est unitaire:

$$ U^\dagger U = \sum_n \sum_m \ket{n} \braket{n' | m'} \bra{m} = \sum_{n,m} \ket{n} \delta_{n,m} \bra{m} = \sum_n \ket{n} \bra{n} = 1 \,. $$

Après un changement de base les coordonnées du ket et les éléments de matrice d’un opérateur son transformés, selon les formules:

$$ \begin{gather*} \ket{\psi'} = U^\dagger \ket{\psi}\,,\quad \psi_n' = \sum_k \braket{n' | k} \psi_k \\ A' = U^\dagger A U \,, \quad A'_{nm} = \sum_{k,l} \braket{n' | k} A_{kl} \braket{l | m'}\,. \end{gather*} $$

Ces deux formules garantissent l’invariance du produit scalaire vis-à-vis des transformations unitaires:

$$ \braket{\psi | A | \psi} = \braket{\psi | U U^\dagger A U U^\dagger | \psi} = \braket{\psi'| A'| \psi'}\,. $$

Un opérateur hermitien $P$ est un projecteur si $P^2 = P$

Le commutateur de deux opérateurs $A,B$ est $[A,B] = AB - BA$, il satisfait les relations:

$$ [A+B,C] = [A,C] + [B,C]\,, \quad [AB,C] = [A,C] B + A [B,C] $$

et l’identité de Jacobi

$$ [A,[B,C]] + [C,[A,B]] + [B,[C,A]] = 0\,. $$

Produit tensoriel

La trace $\Tr$, d’un opérateur est une application linéaire sur les complexes. Elle possède la propriété “cyclique”

$$ \Tr ABC = \Tr CAB = \Tr BCA, $$

avec $A,B,C$ des opérateurs arbitraires. En utilisant la représentation matricielle de l’opérateur $A$ on a la formule explicite

$$ \Tr A = \sum_n A_{nn}, \quad A_{mn} = \braket{m|A|n}, $$

du calcul de la trace, ou, après un changement de base:

$$ \Tr A = \Tr U^\dagger A U = \Tr D = \sum_n a_n, \quad D = \mathrm{a_0, a_1, \ldots} $$

on voit que la trace de $A$ est la somme de ses valeurs propres (spectre).

Le produit de kronecker d’opérateurs $A,B, \ldots$ sur un espace de hilbert a les propriétés suivantes

$$ \begin{gather*} aA \otimes B = A \otimes B, \quad a \in \mathbb{C} \\ A \otimes (B + C) = A\otimes B + A \otimes C \\ (A \otimes B)(C \otimes D) = AC \otimes BD \end{gather*} $$

Le produit $\otimes$ n’est pas commutatif ($A \otimes B \ne B \otimes A$). Il satisfait en outre

$$ \begin{gather*} (A \otimes B)^\dagger = A^\dagger \otimes B^\dagger\\ \Tr( A \times B) = \Tr A\, \Tr B\\ \det(A \otimes B) = (\det A)^{N_A} (\det B)^{N_B}, \quad N_{A,B} = \dim(\mathcal{H}_{A,B}). \end{gather*} $$

Pour calculer explicitement le produit de kronecker on utilise la représentation matricielle des applications et vecteurs. Soient $A$ et $B$ deux matrices de dimensions $\dim(A) = N_A \times M_A$ et $\dim(A) = N_B \times M_B$, leur produit tensoriel est de dimension

$$ \dim(A \otimes B) = (N_AN_B) \times (M_A M_B). $$

Le produit $A\otimes B$ est donc défini par la formule

$$ A \otimes B = \begin{pmatrix} A_{00} B & A_{01} B & \cdots \\ A_{10} B & A_{11} B & \cdots \\ \vdots & \vdots & \ddots \end{pmatrix} , $$

chaque élément de la matrice $A$ est multiplié par la matrice $B$.

La trace partielle satisfait

$$ \Tr_B A \otimes B = A \, \Tr B, $$

où $A$ agit sur $\mathcal{H}_A$ et $B$ sur $\mathcal{H}_B$. plus explicitement, on considère la matrice densité

$$ \rho = \sum_{nm} \rho_{nm} \ket{n}\bra{m} $$

dans la base $\ket{n}$ et on partitionne l’espace d’états en deux parties $A$ et $B$ de dimension $N_A$ et $N_B$, respectivement, tels que $\{n\} = \{n_A\} \cup \{n_B\}$ et de même pour la base de $B$. On peut donc écrire

$$ \rho = \sum_{n_A n_B, m_A m_B} \rho_{n_A n_B, m_A m_B} (\ket{n_A} \otimes \ket{n_B}) (\bra{m_A} \bra{m_B}). $$

La trace partielle sur $B$, donnée par

$$ \rho_A = \Tr_B \rho = \sum_{n_A, m_A} \sum_k \rho_{n_A k, m_A k} \ket{n_A}\bra{m_A}, $$

correspond en physique à l’état (mixte) du sous-ensemble A.

Le qubit: application des postulats de la mécanique quantique

Le qubit est le “quantum” d’information physique: il correspond à l’état d’un système de dimension 2, comme par exemple le spin $1/2$ de l’électron (l’atome d’argent, de valence 1, dans l’expérience de Stern-Gerlach).

Une source crée un faisceau d’atomes Ag (valence 1) qui est envoyé sur un dispositif magnétique qui sépare les atomes selon la direction de leur moment magnétique (orienté ici dans la direction $z$). Stern et Gerlach observèrent une séparation en deux faisceaux qu’on a identifié correspondre aux deux directions du spin de l’électron de valence: “up” (flèche ver le haut $\uparrow$) et “down” (flèche vers le bas $\downarrow$). En sélectionnant les atomes “up”, un deuxième dispositif orienté également selon la direction $z$, ne modifie pas l’orientation du spin.

L’expérience montre que, contrairement au moment magnétique d’un aimant classique, celui de l’électron est quantifié, et ne prend que deux valeurs. En effet, la valeur expérimentale du moment angulaire magnétique, le spin de l’électron, mesuré par Stern-Gerlach est

$$\frac{\hbar}{2}, \quad \hbar = 1.054571821 \, 10^{-34} \,\mathrm{Js}= 1. $$

La première valeur de la constante de Planck est celle du système international d’unités (SI); la deuxième valeur est, dans le cadre du SI, la définition du joule $\mathrm{J}$ en unité de temps (la seconde $\mathrm{s}$).

On peut formaliser le résultat de l’expérience en introduisant $S_z$, l’observable de spin dans la direction $z$. L’opérateur $S_z$ correspond au dispositif SGz, c’est-à-dire la grandeur physique associée à la composante $z$ du spin de l’électron. Il prend deux valeurs:

$$ S_z \ket{\uparrow} = \frac{\hbar}{2} \ket{\uparrow}, \quad S_z \ket{\downarrow} = -\frac{\hbar}{2} \ket{\downarrow}, \quad $$

ce qui exprime le fait que l’application de $S_z$ sur un faisceau dans l’état, noté avec l’étiquette $\uparrow$, nous donne le même état. On a, en multipliant les deux équation par les bras $\bra{\uparrow}$ et $\bra{\downarrow}$,

$$ \braket{\uparrow| S_z | \uparrow} = \frac{\hbar}{2}, \quad \braket{\downarrow| S_z | \downarrow} = -\frac{\hbar}{2}, $$

ou on a utilisé

$$ \braket{\uparrow|\uparrow} = \braket{\downarrow|\downarrow} = 1 \quad \braket{\uparrow|\downarrow} = \braket{\downarrow|\uparrow} = 0 $$

en accord avec le fait que le spin down ne se transforme pas en spin up après le passage par $S_z$. On peut donc associer à l’observable $S_z$ une matrice, et aux états $\uparrow$, $\downarrow$ les coordonnées d’un vecteur:

$$S_z = \frac{\hbar}{2} \sigma_z, \quad \sigma_z = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}, \quad \ket{\uparrow}=\ket{0} = \begin{pmatrix}1 \\ 0\end{pmatrix}, \;\ket{\downarrow}=\ket{1} = \begin{pmatrix}0 \\ 1\end{pmatrix}, $$

où on a défini la matrice de Pauli $\sigma_z$.

Si à la sortie du premier Stern-Gerlach (SGz) on ajoute un SGx orienté selon la direction $x$, le faisceau “up”, se sépare en deux faisceaux $+$ (flèche $\rightarrow$) est $-$ (flèche $\leftarrow$).

En ajoutant au dispositif précédant un troisième SGz, donc en applicant à la source la séquence SGz-SGx-SGz, on récupère deux faisceaux “up” et “down”.

Ces résultats expriment le principe de superposition: le spin “z” est un superposition de deux états de spin “x”, ou inversement, le spin “x” est une superposition de up et down:

$$\ket{\rightarrow} = \ket{0}\braket{0|\rightarrow} + \ket{1}\braket{1|\rightarrow} $$

or, les probabilités de “up” et “down” comme celles de “left” ($\leftarrow$) et “right” ($\rightarrow$) sont égales à 1/2, on peut donc toujours supposer

$$ \ket{\rightarrow} = \ket{+} = \frac{\ket{0} + \ket{1}}{\sqrt{2}}, $$

puisque

$$ |\braket{0|\rightarrow}|^2 = \braket{1|\rightarrow}|^2 = 1/2 $$

$$ |\braket{0|\leftarrow}|^2 = \braket{1|\leftarrow}|^2 = 1/2. $$

Comme les deux résultats $\rightarrow$ et $\leftarrow$ sont excluants, ces deux états sont orthogonaux:

$$ \ket{\leftarrow} = \ket{-} = \frac{\ket{0} - \ket{1}}{\sqrt{2}}. $$

En plus, comme $S_x$ est diagonal dans la base $\ket{\pm}$ on obtient EX:

$$S_x = \frac{\hbar}{2} \sigma_x, \quad \sigma_x = \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}, $$

avec $\sigma_x$ la matrice “x” de pauli.

Un autre point important est que le résultat de la séquence SGz-SGx-SGz est différent de celui de la séquence SGz-SGz-SGx: la conséquence de ce fait expérimental est la non-commutativité des opérateurs de spin dans la direction $x$ et $z$: $[S_x, S_z] \ne 0$. Cette non-commutativité est indicative de la nature physique de spin: les opérateurs de spin sont de générateurs, comme on va le voir plus tard, des rotations, or si on change l’ordre dans lequel on effectue des rotations autour de différents axes on obtient des résultats différents.

Enfin, si on remplace dans la dernière expérience $S_x$ par $S_y$ on obtient la même phénoménologie, le faisceau se sépare toujours en deux avec la même probabilité: on conclue que les trois mesures conduisent à des états physique différents. Si on note $\ket{\oplus}$ et $\ket{\odot}$ les états de l’opérateur $S_y$, on peut supposer

$$ \ket{\oplus} = \frac{\ket{0} + \E^{\I\phi} \ket{1}}{\sqrt{2}}, $$

ce qui est compatible avec

$$ |\braket{\oplus|0}|^2 = |\braket{\oplus|1}|^2 = 1/2. $$

Mais on doit aussi avoir

$$ |\braket{\oplus|+}|^2 = |\braket{\oplus|-}|^2 = 1/2. $$

ce qui implique EX:

$$ \phi = -\pi/2 $$

(le signe $-$ est conventionnel, il selection la règle de la main droite pour les rotations dans l’espace) et

$$S_y = \frac{\hbar}{2} \sigma_y, \quad \sigma_y = \begin{pmatrix}0 & -\I \\ \I & 0\end{pmatrix}. $$

En résumé on a déduit de l’expérience de Stern-Gerlach l’observable du spin 1/2:

$$ \bm S = \frac{\hbar}{2} \bm \sigma $$

avec

$$ \sigma_x = \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}, \quad \sigma_y = \begin{pmatrix}0 & -\I \\ \I & 0\end{pmatrix}, \quad \sigma_z = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}, $$

les matrices de pauli. Le qubit est donc décrit par l’état d’un système quantique de dimension 2, dont la base canonique est donnée par les vecteurs

$$ \ket{0} = \begin{pmatrix}1 \\ 0\end{pmatrix}, \;\ket{1} = \begin{pmatrix}0 \\ 1\end{pmatrix}. $$

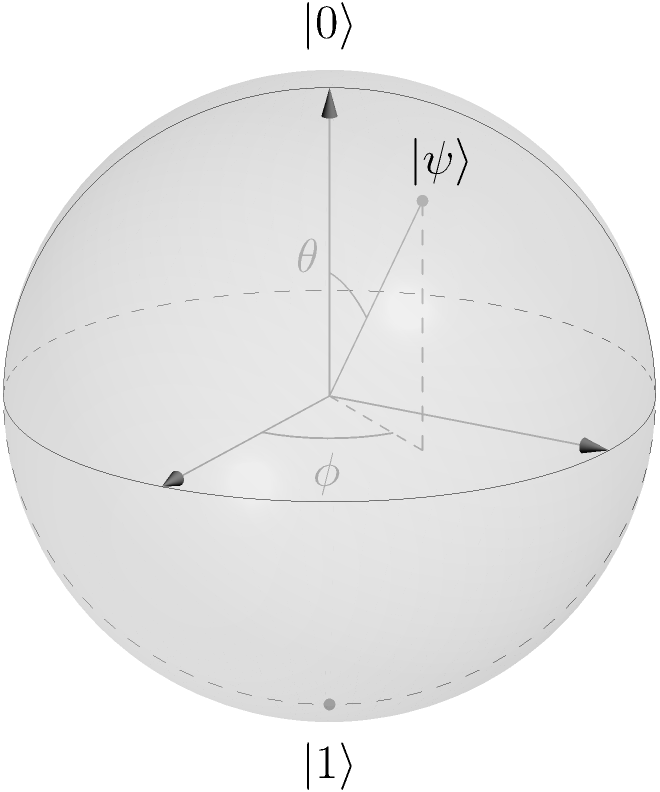
L’état le plus général d’un qubit est la superposition

$$ \ket{\psi} = \cos\frac{\theta}{2} \ket{0} + \E^{\I \phi} \sin \frac{\theta}{2} \ket{1} $$

dépendant des angles sphériques $\theta \in [0, \pi]$ et $\phi \in [0, 2\pi]$. Par exemple, le pôle nord ($\theta = 0$) correspond à l’état $\ket{0}$ et le pôle sud ($\theta = \pi$) à l’état $\ket{1}$.

Géométrie de l’espace de hilbert d’un qubit sous la forme d’une sphère de Bloch.

Quels sont les résultats possibles de la mesure de $S_z$ dans l’état $\ket{\psi}$? On applique la règle de Born pour répondre à la question. Les deux états propres de $S_z$ sont $\ket{0}$ et $\ket{1}$ avec les valeurs propres correspondants $1$ (up) et $-1$ (down). La probabilité de trouver l’état $0$ est donnée par

$$p(0) = |\braket{0|\psi}|^2 = \cos^2 \frac{\theta}{2}, $$

et celle de l’état $1$ est

$$p(1) = |\braket{1|\psi}|^2 = \sin^2 \frac{\theta}{2}. $$

On vérifie que leur somme est 1. La valeur espérée de la composente $z$ du spin est ($\hbar = 1$)

$$ \braket{S_z} = \braket{\psi|S_z|\psi} = \frac{1}{2} \cos \theta $$

Un calcul similaire donne

$$ \braket{S_x} = \braket{\psi|S_z|\psi} = \frac{1}{2} \sin \theta \cos \phi$$

$$ \braket{S_y} = \braket{\psi|S_z|\psi} = \frac{1}{2} \sin \theta \sin \phi. $$

Une transformation unitaire du qubit correspond géométriquement à une rotation dans la sphère de Bloch. Par exemple une rotation du qubit $\ket{0}$ d’un angle $\theta = \pi/2$ autour de l’axe $y$ est donnée par la matrice EX:

$$ R_y(\theta) = \E^{-\I \theta \sigma_y/2} = \cos\frac{\theta}{2} \sigma_0 - \I \sin \frac{\theta}{2} \sigma_x = \begin{pmatrix} \cos\frac{\theta}{2} & -\sin \frac{\theta}{2} \\ \sin \frac{\theta}{2} & \cos \frac{\theta}{2}\end{pmatrix}. $$

avec $\sigma_0 = 1_2$ la matrice identité de dimension 2. On obtiend donc

$$ R_y(\pi/2) \ket{0} = \frac{\ket{0} + \ket{1}}{\sqrt{2}} = \ket{+}. $$

La matrice densité d’un qubit dans l’état générique $\ket{\psi}$ est $\rho = \ket{\psi}\bra{\psi}$ EX:

$$ \rho = \frac{1_2 + \bm n \cdot \bm \sigma}{2} = \frac{1}{2} \begin{pmatrix}1+n_z & n_x - \I n_y \\ n_x + \I n_y & 1 - n_z \end{pmatrix}, $$

où

$$\bm n = (\sin\theta \cos\phi, \sin\theta \sin\phi, \cos\theta), $$

est le vecteur unitaire en coordonnées sphériques.

Le postulat d’évolution nous dit que toute transformation quantique est implémentée par un opérateur unitaire. Considérons un spin sujet à l’action d’un champ magnétique extérieur. Le hamiltonien du système peut s’écrire

$$ H = -\frac{J}{\hbar} S_z, $$

où $J$ est une constante d’énergie proportionnelle au champ appliqué, et S_z le spin de l’électron. l’opérateur d’évolution est

$$ U(t) = \E^{-\I H t/\hbar} = \E^{\I \sigma_z t/2}, $$

avec le choix d’unités $J=\hbar=1$ (l’unité de temps est donc $\hbar/J$):

$$ \quad U(t) = \cos(t/2)\, 1_2 + \I \sin(t/2)\, \sigma_z = \mathrm{diag}(\E^{\I t/2}, \E^{-\I t/2}). $$

Si l’état initial de l’électron est $\ket{+}$, au temps $t$, on a

$$ \ket{\psi(t)} = \frac{\E^{\I t/2}}{\sqrt{2}} \ket{0} + \frac{\E^{-\I t/2}}{\sqrt{2}} \ket{1}. $$

La valeur espérée du spin au cours du temps est EX:

$$ \braket{\bm S(t)} = \braket{\psi(t)| (S_x, S_y, S_z) |\psi(t)} = (\cos t, \sin t, 0), $$

un mouvement de rotation uniforme de fréquence $J/\hbar$ dans le plan perpendiculaire au champ. Il est intéressant d’observer qu’en choisissant $t = \pi/2 \, [\hbar/J]$ on obtient la transformation

$$ \ket{+}\quad \rightarrow\quad \ket{-} = \sigma_x \ket{+}, $$

à un facteur de phase globale près. On peut donc implémenter physiquement l’opération $\sigma_x$, équivalente à l’opération logique de négation $\mathsf{NOT}$, par l’application sur le qubit d’un champ extérieur sur une duration bien précise.

Deux qubits

Selon le principe de composition des espace de hilbert d’un système composite, on doit avoir

$$ \mathcal{H} = \mathcal{H}_1 \otimes \mathcal{H}_1, \quad \dim{\mathcal{H}}_1 = 2, \; \dim{\mathcal{H}} = 2^2. $$

Comme l’ordre des facteurs d’un produit de kronecker est important, le premier terme correspond au premier qubit (A) et le deuxième au (B). On note $\ket{s}$ avec $s \in \{0,1\}$ les kets de base de $\mathcal{H}_1$, on a donc

$$ \ket{s_1} \otimes \ket{s_2} \equiv \ket{s_1s_2} \in \mathcal{H}, \quad s_1, s_2 = 0, 1, $$

les 4 éléments de la base de l’espace de deux spins; notez que $s_1s_2$ est la décomposition binaire de $s=0,1,2,3 \doteq 00, 01, 10, 11$.

La physique de deux particules (quantiques) est bien plus riche que celle d’une seule particule de par la possibilité des interactions. Par exemple, deux spins voisins dont les fonctions d’onde se recouvrent, vont interagir par leur “énergie d’échange” $J$. Soit le hamiltonien de deux spins (Ising)

$$ H = -J \frac{1-\sigma_z}{2} \otimes \frac{1 - \sigma_z}{2}. $$

On peut montrer que l’opérateur d’évolution est EX,

$$ U(t) = \E^{-\I H t} = \mathrm{diag}(1,1,1, \E^{\I t}), $$

($J=\hbar=1$) lequel se réduit pour $t = \pi\, [\hbar/J]$ dans l’opérateur de “phase contrôlée”, puisque le changement sur un qubit dépend de l’état de l’autre:

$$ \mathsf{CZ} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}. $$

Cette interaction entre les deux spins permet de créer un état intriqué: c’est-à-dire un état que ne peut pas s’écrire comme le produit d’un état du premier qubit par celui du deuxième qubit. En effet, l’application de $\mathsf{CZ}$ sur l’état initial produit $\ket{+} \otimes \ket{+} = \ket{++}$ produit l’état

$$ \ket{C} = \mathsf{CZ} \ket{++} = \frac{1}{2}(\ket{00} + \ket{01} + \ket{10} - \ket{11}) $$

qui est intriqué. On peut le vérifier par un calcul explicite, ou en calculant l’état du premier qubit en faisant la trace partielle sur le deuxième EX:

$$ \rho_A = \Tr_B \ket{C}\bra{C} = \frac{1}{2} 1_2, $$

la matrice densité du qubit A est proportionnelle à l’identité. Les éléments diagonaux de $\rho_A$ (dont la somme est bien 1) représentes les probabilités de trouver le qubit up ou down, tandis que les élément non-diagonaux représentent la cohérence quantique de ces deux possibilités. Le fait que ceux-ci soient nuls signifie que l’état du qubit est un état aléatoire sans superposition quantique quelconque. On dit que l’état dont les sous-états sont représentés par une matrice densité proportionnelle à l’identité est un état maximalement intriqué.

Une simple transformation unitaire transforme l’état $\ket{C}$ dans un état de Bell:

$$ \ket{\Phi_+} = (\mathsf{H}\otimes1_2) \mathsf{CZ} \ket{++} = \frac{1}{\sqrt{2}}(\ket{00} + \ket{11}) $$

$$ \mathsf{H} = \frac{\sigma_x + \sigma_z}{\sqrt{2}} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} $$

la matrice de Hadamard. Cet état jour un rôle important dans la téléportation quantique.

Il est intéressant d’observer que, même si l’entropie d’un état pur est nulle, $S = - \braket{\psi| \ln \big(\ket{\psi}\bra{\psi}\big) | \psi} = \ln 1 = 0$, celle associée au premier qubit (idem pour le deuxième — bipartition AB) est maximale:

$$ S_A = - \Tr \, \rho_A \ln \rho_A = -\frac{1}{2} \ln \frac{1}{2} -\frac{1}{2} \ln \frac{1}{2} = \ln 2. $$

L’état (de Bell) correspond donc à un état maximalement intriqué.