$\newcommand{\I}{\mathrm{i}} \newcommand{\E}{\mathrm{e}} \newcommand{\D}{\mathop{}\!\mathrm{d}} \newcommand{\Tr}{\mathrm{tr}} \newcommand{\bra}[1]{\langle{#1}|} \newcommand{\ket}[1]{|{#1}\rangle} \newcommand{\braket}[1]{\langle{#1}\rangle} \newcommand{\bbraket}[1]{\langle\!\langle{#1}\rangle\!\rangle} \newcommand{\bm}{\boldsymbol}$

Cours de mécanique quantique.

Symétries

La symétrie est présente dans pratiquement tout système physique et determine en grande partie ses propriétés et sa dynamique. L’étude de symétries d’un système quantique révèle la géométrie des états quantiques et des ses opérateurs. D’abord, les symétries de l’espace, du temps et de la dynamique, déterminent les lois de conservation et contraignent la forme des états propres des observables comme l’impulsion, le moment angulaire ou l’énergie. Par exemple, les propriétés d’un système physique vis-à-vis de transformations de translation sont liées à l’opérateur d’impulsion; les rotations au moment angulaire; et l’homogénéité temporelle (évolution) au hamiltonien. Plus généralement, un système peut posséder des symétries spécifiques liées à sa géométrie. Dans un cristal, l’invariance par translation devient une symétrie discrète à laquelle correspond une certaine propriété de périodicité des fonctions d’onde; ceci influe, entre autres, sur la propagation de phonons (les quantum de vibration). Dans un métal, près de la surface de Fermi, il existe une symétrie entre les trous et les électrons, la création d’un électron de conduction est accompagné par la création d’un trou dans la quantité de mouvement est opposée à celle de le (quasi) électron. Cette symétrie “électron-trou” est à l’origine du phénomène de supraconductivité. Le ferromagnétisme, ou anti-ferromagnétisme, dépend de la symétrie de fonctions d’onde et du spin. Et cætera.

Mathématiquement la symétrie est associée à un groupe d’opérateurs. Un groupe est un ensemble $\mathcal{U}$ d’éléments $U_1, U_2, \ldots \in \mathcal{U}$ et d’une règle de composition associative (la multiplication) telle que le produit de deux éléments est aussi un élément de $\mathcal{U}$; il existe un élément unité $I$, tel que $IU=U$, ainsi qu’un élément inverse $U^{-1} U =I$, $\forall U \in \mathcal{U}$.

Le sous-groupe $\mathcal{H} \subset \mathcal{U}$ est invariant si pour toute transformation $U \in \mathcal{U}$, la transformation de similitude de $H$ (plus généralement de “conjugaison”), est un élément de $\mathcal{H}$, $UHU^{-1} \in \mathcal{H}$. On écrit $U\mathcal{H}U^{-1}= \mathcal{H}$.

Le groupe de symétrie $\mathcal{U} = \mathrm{sym}(X)$ d’un objet $X$, est généré par l’ensemble de transformation $U$ qui laissent $X$ invariant. Par exemple, soit $X$ un carré, $U$ peut être une rotation $R$ de $\pi/2$ autour de l’axe passant par l’intersection de ses deux diagonales, ou une réflexion $M$ par rapport à une diagonale, etc. On vérifie que l’ensemble de rotations et de réflexions forment un groupe d’ordre 8 (nombre d’éléments du groupe); on vérifie aussi que ces transformations sont toutes reliées par des conjugaisons ($MRM=R'$ ou $RMR^{-1}=M'$) EX.

Symétries du carré ABCD de rotation $R_{1,2,3} = R_z(\phi)$ autour de l’axe $z$ passant par le point d’intersection des diagonales AC et BD et d’angles $\pi/2, \pi$ et $3\pi/4$, et de réflexion $M_{1,2,3,4}$ sur les axes medians et les diagonales.

La notion physique de symétrie correspond à l’invariance des propriétés du système (phases, dynamique) vis-à-vis des transformations par un groupe d’opérateurs associés à chaque symétrie. En particulier, pour un système défini par son hamiltonien $H$, on dit qu’il possède une symétrie $U$ (opérateur unitaire indépendant du temps) si

$$ UHU^\dagger = H, \text{ ou } [U,H] = 0, $$

ce qui implique que la transformation $U$ ne modifie pas l’évolution du système. En effet, la transformation $\ket{\psi'} = U \ket{\psi}$ transforme l’équation de schrödinger dans

$$ \I \frac{\partial}{\partial t} \ket{\psi'} = UHU^\dagger \ket{\psi'} $$

pour l’état $\ket{\psi'}$, identique à celle pour $\ket{\psi}$ si $H$ est invariant vis-à-vis de la transformation $U$.

Avant de discuter les symétries de l’espace nous avons besoin de définir les opérateurs et les états de position et d’impulsion.

Position et impulsion

En mécanique classique la position d’une particule est un vecteur dans l’espace, auquel on associe un référentiel et des coordonnées. En mécanique quantique on doit d’abord définir un espace de hilbert, dont les kets correspondent à l’état “position” de la particule. L’observable position $X$ agit sur les états position $\ket{x}$; la position est donc donnée par ses valeurs propres:

$$ X \ket{x} = x \ket{x}. $$

Notez que du fait que la position est un élément d’un espace de hilbert l’état position est en général une superposition de positions. Un photon qui rentre dans un interféromètre peut bien se “trouver” sur ses deux branches, dans une superposition de deux chemins, et par conséquent, interférer avec “lui même”.

Un modèle simple d‘“espace” est représenté dans la figure ci-dessous.

Modèle discret de l’observable “position” $x$: le réseau à une dimension dont l’unité est $\Delta x = 1$.

Sur cet “espace” la position prend des valeurs discrètes, $x = 0, 1, \ldots, N-1$, ou $N$ est sa longueur totale. L’unité de longueur est prise telle que la distance entre deux positions successives est $\Delta x = 1$. L’opérateur $X$ satisfait donc,

$$ X \ket{x} = x \ket{x}, \quad x = 0, 1, 2, \ldots, N-1, $$

avec l’ensemble $\ket{x}$ (l’état position) formant une base de l’espace position $\mathcal{H}$:

$$ \braket{x|x'} = \delta_{xx'}, \quad \sum_x \ket{x} \bra{x} = 1. $$

La périodicité du réseaux permet d’introduire une deuxième base, $\ket{k}$, reliée à la base position par une transformation de Fourier:

$$ \ket{k} = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} \E^{\I 2\pi k x/N} \ket{x}, $$

ou son inverse, dans laquelle on exprime la position comme une superposition des états $\ket{k}$:

$$ \ket{x} = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} \E^{-\I 2\pi k x/N} \ket{k}. $$

On constate que l’application linéaire qui relie l’espace $x$ et l’espace “k” est

$$ F = \sum_{x,k} \frac{\E^{\I 2\pi k x/N}}{\sqrt{N}} \ket{x} \bra{k} $$

On vérifie aisément que $F$ (la transformation de fourier) est un opérateur unitaire EX. Ceci signifie aussi que les deux équations précédentes sont l’inverse l’une de l’autre:

$$ \ket{x} = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} \E^{-\I 2\pi k x/N} \ket{k} = \sum_{x'} \Big[ \frac{1}{N} \sum_{k} \E^{\I 2\pi k(x'- x)/N} \Big] \ket{x'} = \ket{x} $$

où on a utilisé l’identité

$$ \frac{1}{N} \sum_{k} \E^{\I 2\pi k(x'- x)/N} = \delta_{x,x'}. $$

compatible avec la condition d’orthogonalité $\braket{x|x'} = \delta_{xx'}$ . On déduit également que l’expression du ket $\ket{k}$ dans la base $x$ est

$$ \braket{x|k} = \frac{\E^{\I 2\pi k x/N}}{\sqrt{N}}. $$

On dit qu’on représente le ket $\ket{k}$ dans la base “position” $\ket{x}$; son complexe conjugué est la représentation de la position dans la base “k”, qu’on va identifier avec l’impulsion.

Un vecteur quelconque de l’espace de hilbert $\ket{\psi}$ peut s’exprimer en “base position”, c’est-à-dire comme une superposition des différents états “position”:

$$ \ket{\psi} = \sum_x \psi_x \ket{x}, \quad \psi_x = \braket{x|\psi}, $$

où l’amplitude au carré $|\psi_x|^2$, selon la règle de Born, correspond à la probabilité de trouver le système dans l’état (la position) $x$.

Il est naturel, comme on l’a fait pour la position $x$, d’associer aux nombres $k$ un opérateur $K$ tel que

$$ K \ket{k} = k \ket{k}, \quad \braket{k,k'} = \delta_{kk'}. $$

Pour étudier le lien entre $X$ et $K$, on peut calculer leur commutateur $[X,K]$:

$$ \begin{gather*} \braket{x|XK|x'} = \frac{x}{\sqrt{N}} \sum_{k=0}^{N-1} k \E^{-\I 2\pi k x'/N} \braket{x|k} = \frac{x}{N} \sum_{k=0}^{N-1} k \E^{\I 2\pi k(x - x')/N} \\ \braket{x|KX|x'} = \frac{x'}{\sqrt{N}} \sum_{k=0}^{N-1} k \E^{-\I 2\pi k x'/N} \braket{x|k} = \frac{x'}{N} \sum_{k=0}^{N-1} k \E^{\I 2\pi k(x - x')/N} , \end{gather*} $$

la différence de ces deux équations donne EX

$$ \braket{x|[X,K]|x'} = \frac{x-x'}{\E^{\I 2\pi k(x - x')/N} - 1} $$

où on a fait la somme sur la série géométrique:

$$ \sum_{k=0}^{N-1} k \E^{-\I 2\pi kx/N} = \frac{N}{\E^{-\I 2\pi kx/N}-1} . $$

Quand $x \rightarrow x'$ l’expression tends vers

$$ \lim_{x \to x'} \frac{x-x'}{\E^{\I 2\pi k(x - x')/N - 1}} = \frac{\I N}{2\pi}, $$

ce qui conduit au résultat:

$$ \begin{equation} \label{e:ckp} \Big[X, \frac{2\pi K}{N}\Big] = \I. \end{equation} $$

On observe que le commutateur de $X$ et $K$ est semblable à celui entre la position et l’impulsion (comme grandeurs continues), ce qui confirme l’interprétation de $K$ comme un opérateur impulsion “discret”, opérateur canonique de la position discrète $X$.

On se propose maintenant de généraliser le modèle d’espace discret à un espace continu, dans lequel la position devient un nombre réel avec la dimension de longueur. On introduit donc $L=N\Delta x$ la longueur de la ligne et on remplace $x\Delta x$ par $x \in \mathbb{R}$. La limite continue est définie par

$$ \lim_{\substack{N\rightarrow\infty \\ \Delta x \rightarrow 0}} N\Delta x = L. $$

La variable discrète $k$ devient une variable dimensionnelle donc proportionnelle à $k/\Delta x$, avec l’unité de l’inverse d’une longueur (nombre d’onde, dans l’espace de fourier). En résumé on a

$$ \begin{gather*} N \Delta x \rightarrow L,\\ x \Delta x \rightarrow x,\\ 2\pi k/N\Delta x \rightarrow p/\hbar, \end{gather*} $$

où on a introduit, à la place du nombre d’onde, la variable continue $p$ ayant les dimensions d’une impulsion (avec le choix habituel $\hbar=1$, l’unité d’impulsion devient l’inverse d’une longueur).

Observez que le commutateur de l’équation $\eqref{e:ckp}$, se transforme comme

$$ \Big[X \Delta x, \frac{2\pi K}{N\Delta x}\Big] = [x, p/\hbar] = \I, $$

dans la limite continue.

En faisant $\Delta x \rightarrow 0$ on obtient la limite continue:

$$ \begin{gather*} X \ket{x} = x \ket{x}, \quad \int_{-\infty}^{\infty} \D x\, \ket{x}\bra{x} = 1, \; \braket{x|x'} = \delta(x-x'), \\ P \ket{p} = p \ket{p}, \quad \int_{-\infty}^{\infty} \D p \, \ket{p}\bra{p} = 1, \; \braket{p|p'} = \delta(p-p'), \end{gather*} $$

et (avec la constante de normalization en unité d’action, en accord avec les dimensions de $[\ket{x}] \sim 1/\sqrt{L}$ et $[\ket{p}] \sim \sqrt{L/\hbar}$)

$$ \braket{x|p} = \frac{\E^{\I p x/\hbar}}{\sqrt{2\pi \hbar}}. $$

On montre maintenant que $P$ est l’opérateur d’impulsion. Pour cela on calcule le commutateur de $P$ avec $X$. L’opérateur $P$ exprimé en base $x$ est

$$ \begin{align*} \braket{x|P|x'} &= \int_{-\infty}^{\infty}\D p \,\braket{x|P|p} \braket{p|x'} \\ & = \int_{-\infty}^{\infty}\D p \, p \braket{x|p} \braket{p|x'} \\ & = \Big(- \I \hbar \frac{\partial }{\partial x} \Big) \int_{-\infty}^{\infty} \frac{\D p}{2\pi\hbar} \, \E^{\I p x/\hbar} \E^{-\I p x'/\hbar} \\ & = -\I \hbar \frac{\partial }{\partial x} \delta(x-x')\,, \end{align*} $$

ce qui est bien en accord avec l’identification habituelle de l’opérateur impulsion $P=-\I\hbar \D/\!\D x$, comme opérateur différentiel. Par conséquent, on a

$$ \begin{align*} \bra{x} XP \ket{x'} &= -x \I\hbar \frac{\partial }{\partial x} \delta(x-x')\\ \bra{x} PX \ket{x'} &= -x' \I\hbar \frac{\partial }{\partial x} \delta(x-x'), \end{align*} $$

et, en faisant la différence,

$$ \bra{x}[X,P]\ket{x'} = - (x-x')\I \hbar \frac{\partial }{\partial x}\delta(x-x') = \I\hbar\delta(x-x') $$

où on a utilisé la propriété de la dérivée de la delta de Dirac:

$$ x \frac{\D}{\D x}\delta(x)= - \delta(x), $$

ce qui conduit à l’expression du commutateur,

$$ \begin{equation} [X,P] = \I \hbar, \end{equation} $$

résultat qui correspond bien avec l’interprétation de $P$ comme l’opérateur d’impulsion.

Comme dans le cas discret, on utilise la base $x$ pour développer l’état de la “particule”:

$$ \ket{\psi} = \int_0^\infty \D x \psi(x) \ket{x}, \quad \psi(x) = \braket{x|\psi}, $$

où maintenant $\psi(x)$ est la fonction d’onde de la particule et $|\psi(x)|^2$ représente la densité de probabilité, ou distribution spatiale, de la particule. En utilisant l’équation de schrödinger pour $\ket{\psi}$ il est facile de démontrer EX

$$ \I \frac{\partial}{\partial t} \psi(x,t) = \hat{H} \psi(x,t), \quad \braket{x'|H|x} = \hat{H}\delta(x'-x) $$

avec $\hat{H}$ le hamiltonien en représentation position (opérateur différentiel).

Translation

On définit l’opérateur de translation $T_a$ par

$$ T_a \ket{x} = \ket{x+a}, \quad a \in \mathbb{R}, $$

où $a$ est le paramètre de translation du point $x$ vers le point $x+a$. On vérifie aisément que la famille d’opérateurs $T_a$ forme un groupe:

$$ \begin{gather*} T_aT_b \ket{x}=\ket{x+a+b}= T_bT_a\ket{x} = T_{a+b}\ket{x} \\ T_aT_{-a} \ket{x} = \ket{x} = T_a T_a^{-1} \ket{x}, \end{gather*} $$

avec $T_0$ l’élément unité et $T_{-a}$ l’élément inverse; en plus, comme $T_aT_b=T_bT_a$ le groupe est abélien (commutatif).

Translation de la fonction d’onde $\psi(x) = \braket{x|\psi} \rightarrow \braket{x|T_a|\psi} = \psi'(x)$.

Voyons comment $T_a$ agit sur la fonction d’onde (voir la figure ci-dessus):

$$ \begin{align*} \braket{x|T_a|\psi} &= \int \D x'\, \braket{x|T_a|x'} \braket{x'|\psi} = \\ &= \int \D x'\, \braket{x|x'+a} \psi(x') = \int \D x'\, \delta(x - a - x') \psi(x') \\ &= \psi(x-a) = \braket{x-a|\psi}, \end{align*} $$

elle conserve donc sa forme $\psi(x)$, mais déplacée de $a$: l’expression $\braket{x-a|\psi}$ représente le vecteur $\ket{\psi}$ dans la base position déplacée de $-a$. On observe que le complexe conjugué de l’expression précédente peut s’écrire

$$ \braket{x|T_a|\psi}^\star = \braket{\psi|x-a} =\braket{\psi|T_a^\dagger|x} = \braket{\psi|T_{-a}|x} \quad \Rightarrow \quad T^\dagger_a = T^{-1}_a, $$

ce qui implique l’unitarité de $T_a$. Par conséquent, pour un déplacement infinitésimal $\Delta x$, $T_{\Delta x}$ doit être proche de l’unité ($T_0=1$):

$$ T_{\Delta x} = 1 - \I \Delta x K, \quad K = K^\dagger, $$

avec $K$ un certain opérateur hermitien. En effet, en posant $a = N\Delta x$, on a dans la limite continue

$$ T_a = \lim_{N \to \infty} \Big(1 - \I \Delta x K \Big)^N = \E^{-\I a K}, $$

une succession de $N$ translations de $\Delta x$ résulte bien dans une translation de $a$. On va maintenant démontrer que $K$ est en fait (à une constante dimensionnelle près) l’opérateur d’impulsion. Pour cela on calcule le commutateur $[X,T]$:

$$ \begin{align*} X T_{\Delta x} \ket{x} &= (x + \Delta x)\ket{x + \Delta x} \\ &= X(1 - \I \Delta x K) \ket{x} = x\ket{x} - \I \Delta x XK \ket{x}, \end{align*} $$

$$ \begin{align*} T_{\Delta x} X \ket{x} &= x\ket{x + \Delta x} \\ &= x(1 - \I \Delta x K) \ket{x} = x\ket{x} - \I \Delta x KX \ket{x}, \end{align*} $$

leur différence (à l’ordre $\Delta x$) est

$$ (X T_{\Delta x} - T_{\Delta x} X) \ket{x} = \Delta x \ket{x} = -\I \Delta x (XK -KX) \ket{x}, $$

ce qui implique,

$$ [X,K] = \I \quad \Rightarrow \quad K = \frac{P}{\hbar}, $$

où on a utilisé le commutateur position-impulsion pour identifier $P$. En définitive, l’opérateur de translation s’écrit:

$$ T_{\bm a} = \E^{-\I \bm a \cdot \bm P/\hbar}, \quad \bm a \in \mathbb{R}^3, $$

en généralisant le résultat en dimension 1, à trois dimensions de l’espace (les translations sur différentes direction commutent).

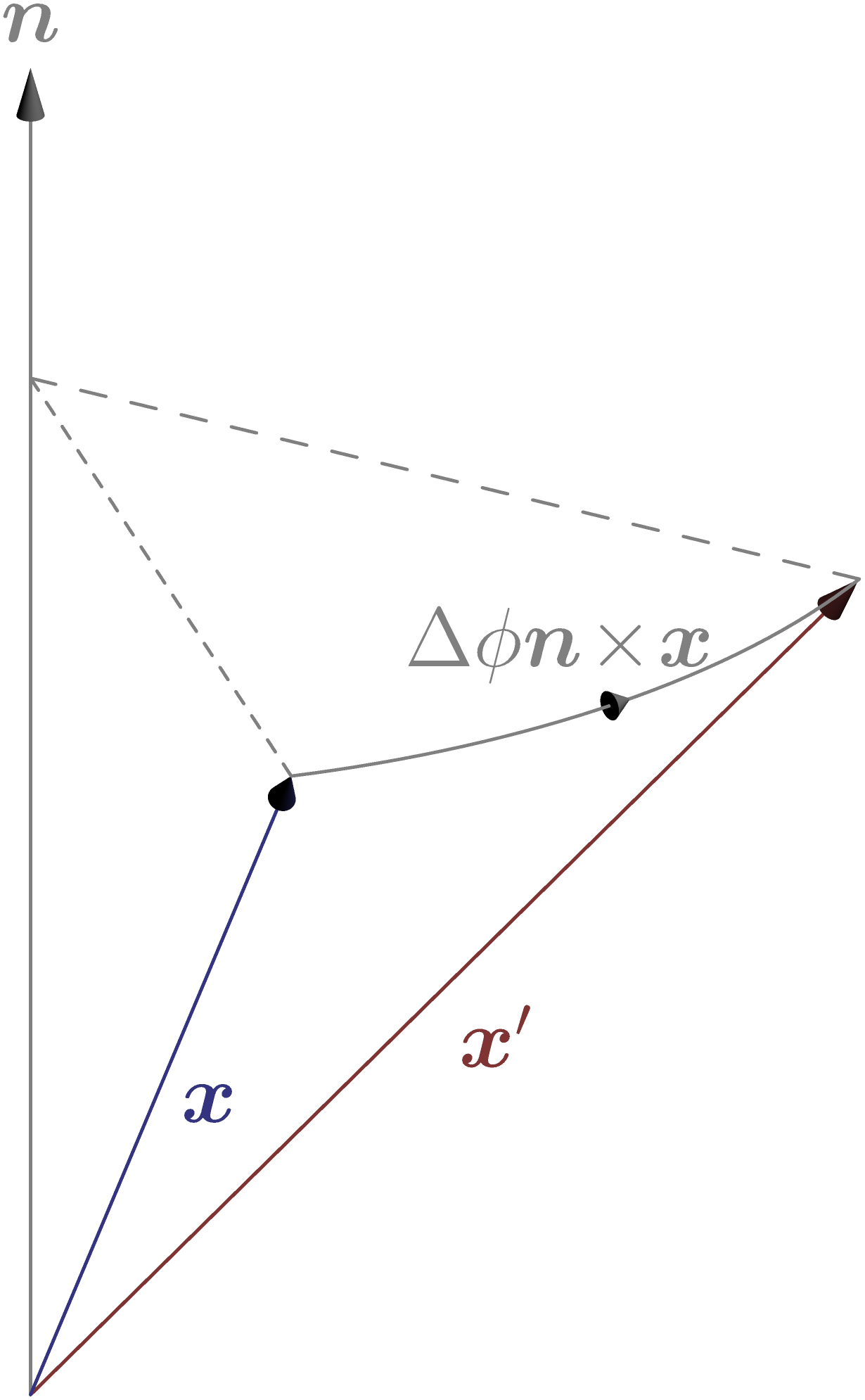
Rotation

La rotation d’un vecteur $\bm x$ en $\mathbb{R}^3$ est spécifiée par un axe $\bm n$ et un angle $\Delta \phi$: $\bm x' = \bm x + \Delta \bm \phi \times \bm x$ (avec $\Delta \bm \phi = \Delta \phi \bm n$, où $\bm n$ est de longueur unité).

On définit l’opérateur de rotation par

$$ R_{\bm n}(\phi) \ket{\bm x} = \ket{\bm x + \bm \phi \times \bm x}. $$

Pour une rotation infinitésimale $\Delta \phi$, $R_{\bm n}(\Delta \phi)$ est proche de l’unité:

$$ R_{\bm n}(\Delta \phi) = 1 - \I \Delta \bm\phi \cdot \bm M, \quad \bm M = \bm M^\dagger $$

où $\bm M$ est un opérateur hermitien sans dimension, tel que

$$ \begin{align*} R_{\bm n}(\Delta \phi) \ket{\bm x} &= (1-\I \Delta \bm\phi \cdot \bm M) \ket{x} = \ket{\bm x + \Delta \phi \bm n \times \bm x} \\ &= \Big[1 - \frac{\I}{\hbar} (\Delta \phi \bm n \times \bm x) \cdot \bm P \Big] \ket{\bm x} \\ &=\Big[1 - \frac{\I}{\hbar} \Delta \bm\phi \cdot (\bm X \times \bm P) \Big] \ket{\bm x} \end{align*} $$

ou, par analogie avec la translation de $\Delta \bm x = \Delta \phi \,\bm n\times \bm x$ on a introduit l’impulsion $\bm P/\hbar$; on a aussi remplacé $\bm x$ par $\bm X$ et utilisé la propriété cyclique du produit mixte (notez que dans le produit vectoriel les composantes de $\bm X$ et $\bm P$ sont toujours sur des directions différentes, ce qui permet d’en échanger l’ordre). En comparant la première et dernière lignes, on obtient $\bm M = \bm L /\hbar$,

$$ \bm L = \bm X \times \bm P $$

qui est l’opérateur du moment angulaire. On conclue que l’opérateur de rotation s’écrit:

$$ R_{\bm n}(\phi) = \E^{-\I \phi \bm n \cdot \bm L/\hbar}. $$

Il est important d’observer que l’opérateur $\bm L$ est un générateur de la rotation, ainsi comme $\bm P$ en est pour la translation; il ne dépend pas des paramètres de la rotation $\bm n$ et $\phi$, par conséquent, il peut être déterminé en étudiant une rotation infinitésimale, comme on vient de le faire. Nous pouvons appliquer cette idée à la rotation dans l’espace, c’est-à-dire le moment angulaire correspondant au nombre orbital $l=1$, comme on va le voir:

$$ \bm x \quad \rightarrow \quad \bm x + \Delta \bm x, \; \Delta x = \Delta \phi \bm n \times \bm x = -\frac{\I}{\hbar} \Delta \phi \bm n \cdot \bm L \bm x. $$

La dernière égalité introduit les matrices:

$$ \bm n \cdot \bm L = \I\hbar\begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}, \quad \bm x = \begin{pmatrix} x \\ y \\ z \end{pmatrix}, $$

ce qui implique

$$ L_x = \hbar \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -\I \\ 0 & \I & 0 \end{pmatrix}, \; L_y = \hbar \begin{pmatrix} 0 & 0 & \I \\ 0 & 0 & 0 \\ -\I & 0 & 0 \end{pmatrix}, \; L_z = \hbar \begin{pmatrix} 0 & -\I & 0 \\ \I & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}. $$

Les matrices de rotation selon les axes $(x,y,z)$ sont donc EX

$$ R_x(\phi) = \begin{pmatrix}1 & 0 & 0 \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi & \cos\phi \end{pmatrix}, \; R_y(\phi) = \begin{pmatrix}\cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{pmatrix}, \; R_z(\phi) = \begin{pmatrix}\cos\phi & -\sin\phi & 0\\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \end{pmatrix}. $$

On vérifie par calcul direct les relations de commutation EX:

$$ [L^2, \bm L] = 0, \quad [L_x, L_y] = \I\hbar L_z, \; [L_z, L_x] = \I\hbar L_y, \; [L_y, L_z] = \I\hbar L_x, $$

qui sont en fait parfaitement générales pour tout moment angulaire. Comme le commutateur $[L^2, L_z] = 0$ s’annule, on peut choisir une base commune de $L^2$ et $L_z$, qu’on note $\ket{l,m}$: on dit que $z$ est l’axe de quantification du moment angulaire:

$$ \begin{gather*} L^2 \ket{l,m} = \hbar^2 l(l+1) \ket{j,m}\\ L_z \ket{j,m} = \hbar m \ket{j,m}, \end{gather*} $$

ici $l$ est le nombre quantique orbital, et $m$ le nombre quantique magnétique, dénominations utilisées pour décrire la structure électronique des atomes.

On se propose maintenant de calculer $l$, $m$ et les vecteurs propres $\ket{l,m}$. Les valeurs propres de $L_z$ sont $m=-1,0,1$, et celles de $L^2$ sont toutes égales à $2$ (troi,s fois dégénérée),

$$ L^2 = \hbar \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{pmatrix}, $$

ce qui correspond à $l=1$, comme on l’avait anticipé pour les rotations dans l’espace. On constate donc que l’espace de hilbert du moment angulaire $\bm L$ avec $l=1$ est simplement tridimensionnel, il ne prend que trois valeurs possibles $-\hbar, 0, \hbar$. Les vecteurs propres sont EX:

$$ \ket{1,-1} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -\I \\ 0 \end{pmatrix}, \; \ket{1,0} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, \; \ket{1,1} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ \I \\ 0 \end{pmatrix}\dots $$

En identifiant $\braket{\theta,\phi|j,m} = \braket{\bm n| j,m}$ (les états propres de $L^2$ et $L_z$ en représentation position) avec le produit scalaire des vecteurs propres et de l’axe $\bm n$, on obtient

$$ \begin{gather*} \braket{\bm n|1,-1} = \frac{1}{\sqrt{2}} \E^{-\I\phi} \sin\theta, \\ \braket{\bm n|1,0} = \cos\theta, \\ \braket{\bm n|1,1} = -\frac{1}{\sqrt{2}} \E^{\I\phi} \sin\theta, \end{gather*} $$

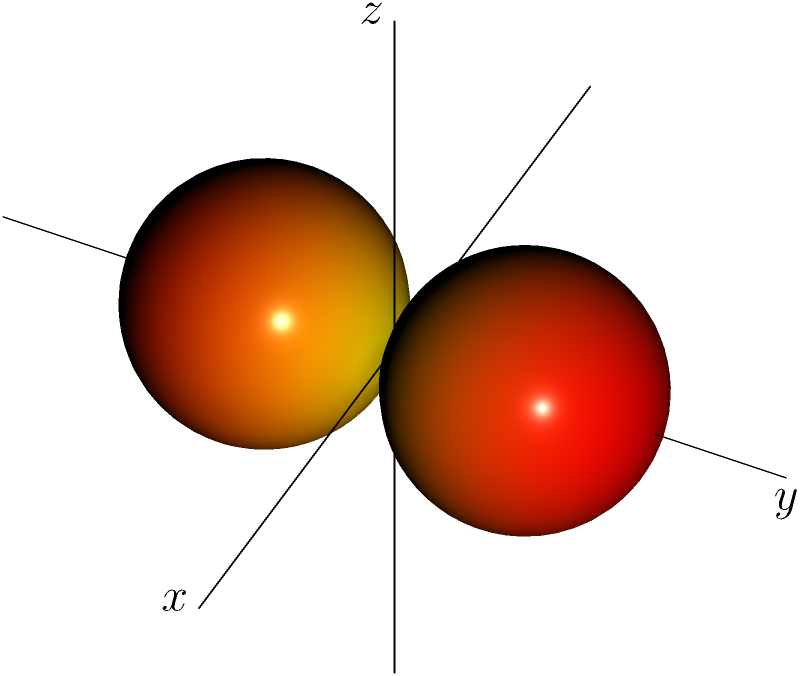
expressions, à des facteurs de normalisation près, correspondant aux harmoniques sphériques $Y_{lm}(\theta, \phi)$:

$$ \braket{\bm n| l,m} \sim Y_{lm}, \quad l=1, \; m = -1, 0, 1. $$

Harmonique sphérique $(l,m)=(1,-1)$.

Ces fonctions représentent la distribution angulaire de l’amplitude de probabilité (fonction d’onde) de la particule, dans le cas de l’atome par exemple.